माना T किसी समतल में स्थित समस्त त्रिभुजों का एक समुच्चय है। समुच्चय T में R = {(T1,T2):T1,T2 के सर्वांगसम है} एक संबंध है। सिद्ध कीजिये कि R एक तुल्यता संबंध है।
दिया गया संबंध है:
R= {(T1,T2):T1T2 के सर्वांगसम है तथा T1,T2∈T जहाँ T समतल में स्थित त्रिभुजों का समुच्चय है।
आइए आगे स्वतुयता, सममितता व संक्रामकता की जाँच करते है -
स्वतुल्यता :
माना, T1,T में स्वेच्छ त्रिभुज है, तब T1 स्वयं के सर्वांगसम है क्योकि प्रत्येक त्रिभुज स्वयं के सर्वांगसम होते है।
⇒(T1,T1)∈R
∴R,T में स्वतुल्य है।
सममितता:
माना, T1,T2∈T इस प्रकार है कि,
(T1,T2)∈R
⇒T1,T2 के सर्वांगसम है।
∴ ⇒T2,T1 के सर्वांगसम है।
⇒(T2,T1)∈R
∴ R,T में सममित है।
संक्रामकता:
माना, T1,T2,T3∈T इस प्रकार है कि,
(T1,T2)∈R और (T2,T3)∈R
तब, T1,T2 के सर्वांगसम है और T2,T3 के सर्वांगसम है।
अतः T1,T3 के सर्वांगसम है।
⇒(T1,T3)∈R
∴R,T में संक्रामक है।
चूँकि संबंध R स्वतुल्य, सममित और संक्रामक है अत: R एक तुल्यता संबंध है।
Topper's Solved these Questions
- संबंध BOOK - PRABODH PUBLICATIONCHAPTER - संबंध EXERCISE - प्रश्नावली 1.1
12 Videos
- संबंध BOOK - PRABODH PUBLICATIONCHAPTER - संबंध EXERCISE - प्रश्नावली 1.2
8 Videos
- वर्धमान और ह्रासमान फलन BOOK - PRABODH PUBLICATIONCHAPTER - वर्धमान और ह्रासमान फलन EXERCISE - प्रश्नावली 15.2
37 Videos
- संबंध और फलन BOOK - PRABODH PUBLICATIONCHAPTER - संबंध और फलन EXERCISE - दीर्घ उत्तरीय प्रश्न
36 Videos
Similar Questions
माना समुच्चय A={1,3,5,7} में एक संबंध R इस प्रकार परिभाषित है कि R={(x,y):y=x+2}. संबंध R को क्रमित युग्मो के समुच्चय के रूप में लिखिए|
View Solutionसिद्ध कीजिये कि पूर्णको के समुच्चय Z में परिभाषित संबंध R,(a,b)∈R⇔a−b,5 से विभाज्य है, एक तुल्यता संबंध है।
View Solutionसिद्ध कीजिए कि फलन f(x)=x3−6x2+12x−18 पर एक निरंतर वधमान फलन है।
View Solutionसिद्ध कीजिए कि समुच्चय {1,2,} में R={(1,1),(2,2),(3,3),(1,2),(2,3)} द्वारा प्रदत्त संबंध स्वतुल्य है परन्तु न तो सममित है और न संक्रामक है।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
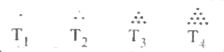
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View Solutionकृष्णिका विकिरण के लिए निम्न में से कौन सा वक्र सही है? (दिया गया है: T_(1) lt T_(2) lt T_(3) lt T_(4))
View Solutionविरंजक चूर्ण में इसके एक घटक के रूप में एक ऑक्सोअम्ल का लवण होता है। इस अम्ल का एनहाइड्राइड है:
View Solutionएक एकपरमाण्विक वास्तविक गैस का एक मोल समीकरण p (V — b) = RT को संतुष्ट करता है जहाँ b एक स्थिरांक है। गैस के लिए अंतरापरमाणुक विभव V(r) और अंतरापरमाणुक दूरी r का संबंध निम्नानुसार दर्शाया जाता है
View Solutionदिया गया है कि n कोटि की अभिक्रिया के लिए दर समीकरण का समाकलित रूप k=1/(t(n-1))[1/(C^(n-1))-1/(C_0^(n-1))] है जहाँ C_0 और C प्रारंभ में और समय t के बाद अभिकारक सांद्रता के मान हैं। t_(3/4) और t_(1/2) के मध्य क्या संबंध है जहाँ t_(3/4) , C के ""^(1/4)C_0 होने के लिए आवश्यक समय है।
View Solutionविभिन्न परिस्थितियों में एक आदर्श गैस को (p_(1), V_(1), T_(1)) से (p_(2), V_(2), T_(2)) तक प्रसारित किया जाता है। निम्नलिखित में से गलत कथन है?
View SolutionNi^(2+) के एक दुर्बल क्षेत्र संकुल का चुंबकीय आघूर्ण 2.82 BM है। Ni^(2+) के t_(2g) स्तर में इलेक्ट्रॉन की संख्या होगी -
View Solution
