एक क्षैतिज तल में एक-दूसरे से L दूरी पर दो बिंदुओं A तथा B के बीच एक मोटा तार बँधा है। तार में कोई तनाव नहीं है। तार की अनुप्रस्थ काट का क्षेत्रफल A है तथा उसके पदार्थ का यंग मॉड्युलस Y है। इस तार के मध्यबिंदु C से W भार की एक वस्तु लटकाई गई है, जिससे वह बिंदु कुछ नीचे आ जाता है। संतुलन की अवस्था में तार के दोनों हिस्सों का AB के साथ कोण θ निकालें।
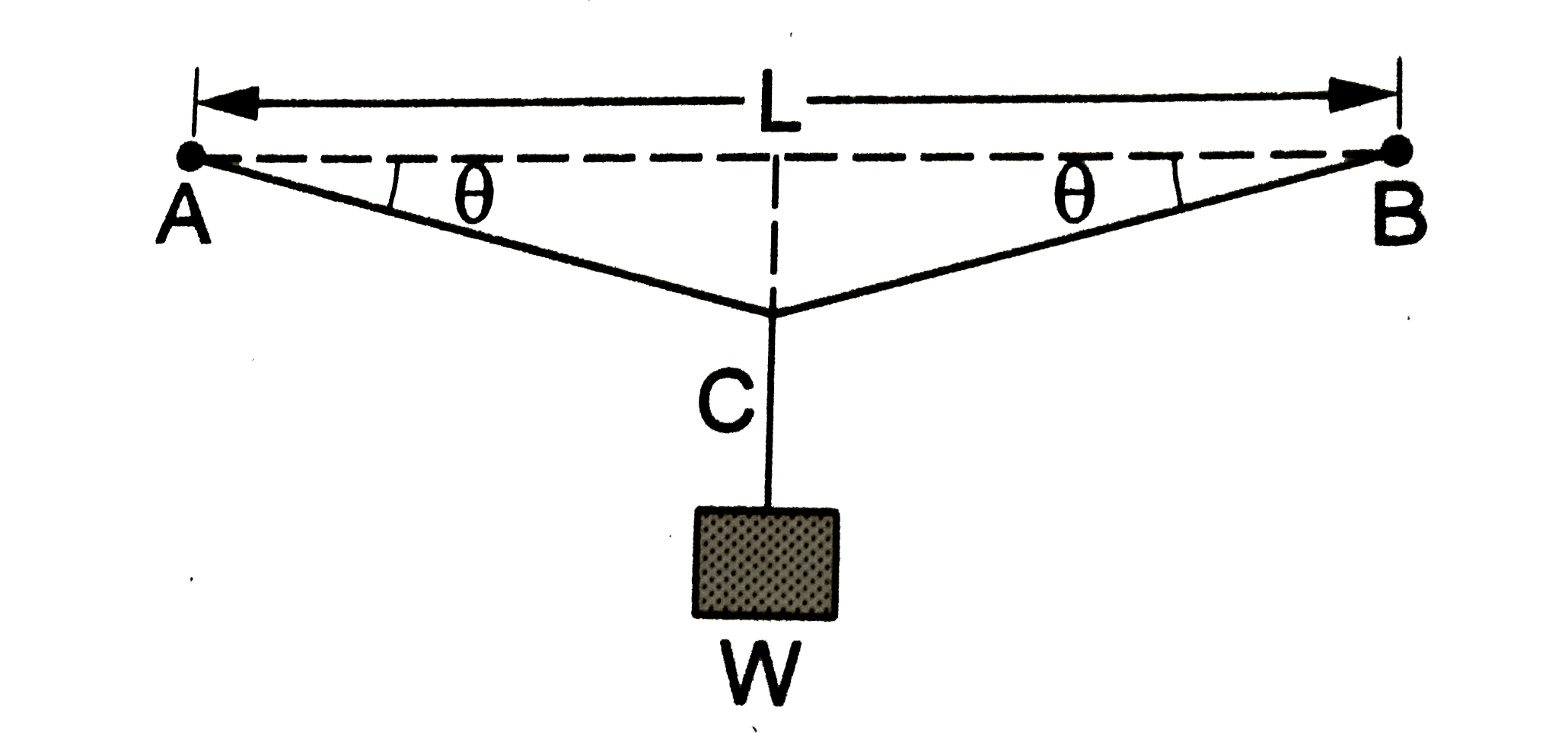
मान लें कि तार में तनाव T हो जाता है। तार के मध्यबिंदु के कण के संतुलन के लिए,
2Tsinθ=W,
प्रतिबल =TA=W2Asinθ ... (i)
तार की बढ़ी हुई लंबाई =2.AC=2.(L2)1cosθ=Lcosθ
तार की लंबाई में वृद्धि =Lcosθ−L=L(1−cosθ)cosθ
अतः, विकृति =1−cosθcosθ ... (ii)
चूँकि प्रतिबल =Y× विकृति,
W2Asinθ=Y×1−cosθcosθ [समीकरण (i) एवं (ii) से]
या W2AY=sinθ(1−cosθ)cosθ
चूँकि तार मोटा है, अतः तार का क्षैतिज से झुकाव θ भी छोटा होगा। sinθ≈θ तथा cosθ≈1−θ22 का उपयोग करने पर,
W2AY≈θ321−θ22=θ32(1−θ22)−1
≈θ32(1+θ22)≈θ32
अतः, θ=(WAY)1/3 रेडियन।
Topper's Solved these Questions
- प्रत्यास्था BOOK - HC VERMA HINDICHAPTER - प्रत्यास्था EXERCISE - विचार हेतु प्रश्न
3 Videos
- प्रत्यास्था BOOK - HC VERMA HINDICHAPTER - प्रत्यास्था EXERCISE - सटीक उत्तरवाले प्रश्न I
11 Videos
- प्रत्यास्था BOOK - HC VERMA HINDICHAPTER - प्रत्यास्था EXERCISE - अभ्यास के प्रश्न
13 Videos
- प्रकाशमितिBOOK - HC VERMA HINDICHAPTER - प्रकाशमितिEXERCISE - अभ्यास के प्रश्न
11 Videos
- बल-आघूर्ण BOOK - HC VERMA HINDICHAPTER - बल-आघूर्ण EXERCISE - अभ्यास के प्रश्न
45 Videos
Similar Questions
एक धातु के तार के कम विरूपण के लिए प्रतिबल/विकृति का मान अचर होता है। यदि विरूपण अधिक कर दिया जाए, तो यह अनुपात बढ़ेगा या घटेगा?
View Solution1 cm त्रिज्या वाली एक रस्सी में तनाव 500 N से ज्यादा करने से वह टूट जाती है। उसी प्रकार की 2 cm त्रिज्या वाली रस्सी में अधिकतम कितना तनाव उत्पन्न किया जा सकता है, ताकि वह नहीं टूटे?
View Solutionअनुप्रस्थ परिच्छेद 4mm2 तथा लंबाई 3 m वाले एक धातु के तार से 10 kg की वस्तु लटकाई गई है। तार के पदार्थ का यंग मॉड्युलस 2.0×1011N/m2 है। ज्ञात करे, (a) प्रतिबल, (b) अनुदैर्ध्य विकृति तथा (c) लंबाई में वृद्धि।
View Solutionप्रकाश का एक स्त्रोत 15 s में 45 J ऊर्जा उत्सर्जित करता है । इसका विकिरत फ्लक्स कितना है ?
View Solutionm द्रव्यमान का एक कण μ चाल से क्षैतिज से θ कोण पर प्रक्षेपित किया गया है। जब कण उच्चतम बिंदु पर है, उस समय प्रक्षेपण-बिंदु के परितः इसके भार का बल-आघूर्ण ज्ञात कीजिए
View Solutionएक लम्बे सीधे तार में बहने वाली धारा 1 ऐम्पियर है। चुंबकीय क्षेत्र की तीव्रता 10−5 वेबर/मीटर2 होगी तार से :
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solution52 पत्तो की एक भाँति फेंटी गई गड्डी में एक पत्ता खो जाता है। शेष पत्तो से दो पत्ते निकाले जाते है नो ईंटके पत्ते है । खो गए पत्ते के ईंट का पत्ता होने की प्रायिकता है ?
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionयदि 5m तार को 8 भागों में विभाजित करते है तो हर एक भाग की लम्बाई ज्ञात करो।
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solutionएक 713 मीटर लम्बे तार को 7 बराबर भागों में काटा जाता है तब प्रत्येक भाग की लम्बाई होगी
View Solution
