रोटर नामक यंत्र में खोखली बेलनाकार संचरना अपने अक्ष में परित: घूमती है और एक मनुष्य उसकी भीतरी दीवार के सहारे संचरना के फर्श पर खड़ा होगा है। संचरना का कोणीय वेग धीरे-धीरे बढ़ाया जाता है और जब यह वेग एक खास मान तक पहुँच जाता है तो नीचे से फर्श हटा लिया जाता है। ऐसे में मनुष्य दीवार के सहारे, पर बिना किसी फर्श के टिका रहता है। यदि रोटर की त्रिज्या 2 m तथा मनुष्य और दीवार के बीच घर्षण गुणांक 0.2 हो तो रोटर का न्यूनतम कोणीय वेग ज्ञात करे जब फर्श हटाया जा सके। g का मान 10m/s2 है।
प्रश्न में दी हुई परिस्थिति चित्र 10.W7 में दिखाई गई है। जब फर्श को हटा देते है तब मनुष्य पर लगते बल है,
(a) भार mg ,नीचे की ओर,
(b) दीवार द्वारा मनुष्य पर अभिलंब बल N केंद्र की ओर तथा
(c) दीवार द्वारा मनुष्य पर घर्षण बल fs ऊपर की ओर।
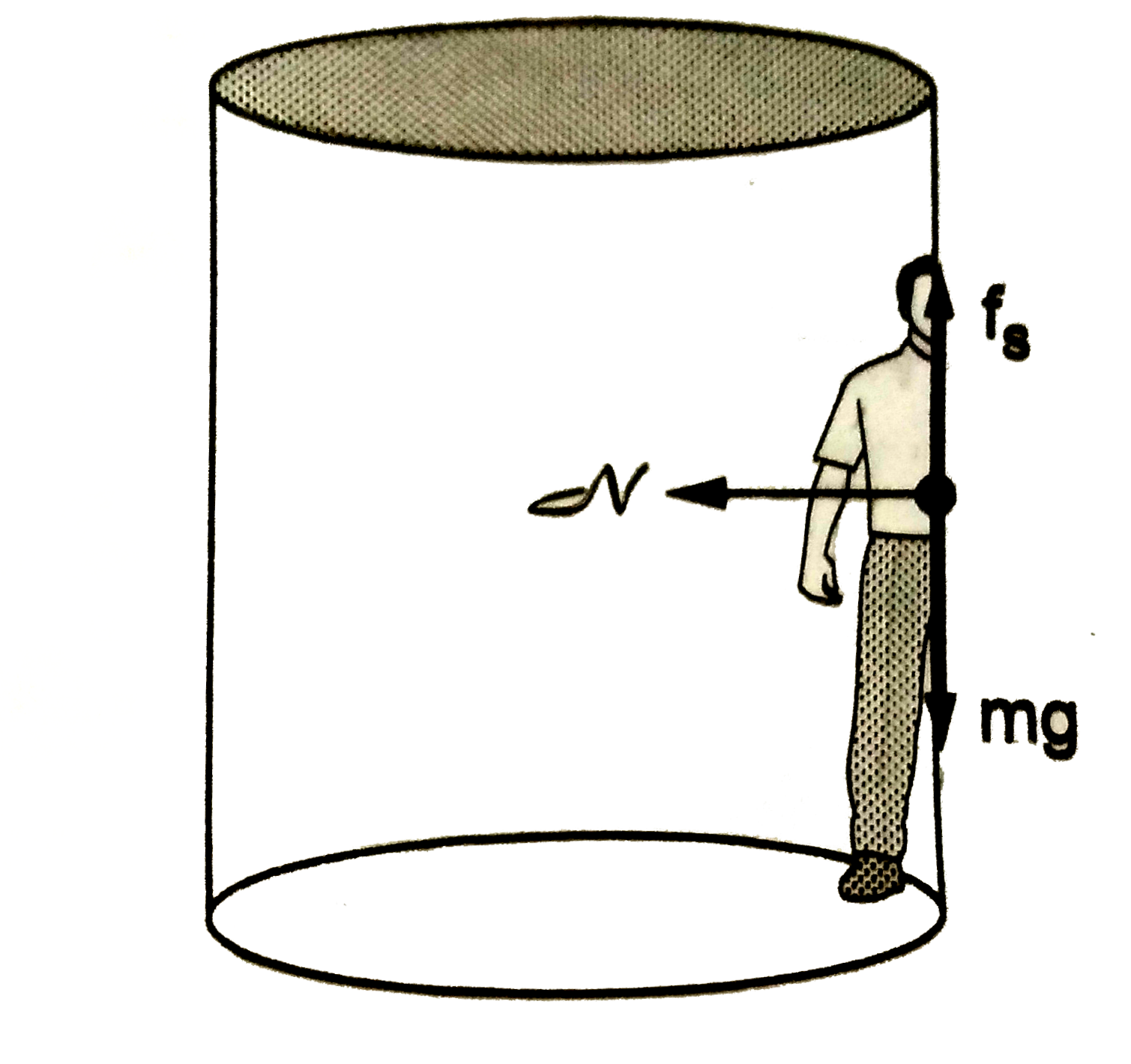
मनुष्य एक वृत्ताकार पथ पर ω2R त्वरण से चल रहा है। केंद्र की ओर तथा ऊपर की ओर बलों के घटक लेकर न्यूटन के गति-नियम लगाने पर,
N=mω2r तथा fs=mg
रोटर के न्यूनतम वेग के लिए घर्षण का मान सीमांत घर्षण के बराबर होगा। अतः,
μs=fsN=gω2r
या ω=√gμsr=√10m/s20.20×2m=5rad/s
Topper's Solved these Questions
- वृत्त में गति BOOK - HC VERMA HINDICHAPTER - वृत्त में गति EXERCISE - अभ्यास 10.1
1 Videos
- वृत्त में गति BOOK - HC VERMA HINDICHAPTER - वृत्त में गति EXERCISE - अभ्यास 10.2
1 Videos
- लेंस-आधारित उपकरण BOOK - HC VERMA HINDICHAPTER - लेंस-आधारित उपकरण EXERCISE - अभ्यास के प्रश्न
26 Videos
- संवेग- संरक्षण का सिद्धांत, टक्कर BOOK - HC VERMA HINDICHAPTER - संवेग- संरक्षण का सिद्धांत, टक्कर EXERCISE - अभ्यास के प्रश्न
57 Videos
Similar Questions
एक कण 20 cm त्रिज्या वाले वृत्त पर रेखीय वेग 10 m/s से चल रहा है। कण का कोणीय वेग निकाले।
View Solutionएक कण 20 cm त्रिज्या के वृत्त पर चल रहा है। इसकी चाल एकसमान दर से बढ़ती जाती है। यदि चाल 2.0 s में 5.0 m/s से 6.0 m/s हो जाती है, तो कण का कोणीय त्वरण का मान बताएँ।
View Solutionएक मनुष्य खुले स्थान में चार अलग-अलग वृक्षों को देखता है जिनकी ऊँचाइयाँ तथा दूरियाँ नीचे दी गई है। इन वृक्षों को उनकी आभासी ऊँचाइयों के घटते क्रम में लगाएँ।

View Solution1.0 kg तथा 4.0kg द्रव्यमानों के दो कणों की गतिज ऊर्जाएँ बराबर हैं। इनके रैखिक संवेगों का अनुपात ज्ञात कीजिए।
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionजब AgNO_(3) के विलयन को आधिक्य में CoCl_(3).XNH_(3) विलयन के 1M में मिलाया जाता है, तो AgCI के एक मोल का निर्माण होता है? 'X' का मान क्या है? (माना लीजिए कि उपसहसंयोजन संख्या 6 है।)
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@) = 0.4 और P_(B)^(@) = 1.2 atm है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View Solutionजब logk और 1/T के बीच एक आलेख आलेखित किया जाता है, तो हमें एक आलेख प्राप्त होता है, जैसा कि नीचे दर्शाया गया है आलेख में ढाल का मान क्या है?
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View Solutionएक यौगिक (A) का उपयोग सॉल्वे प्रक्रम में अमोनिया की पुनः प्राप्ति के लिए धावन सोडा के विचरन में किया जाता है। जब CO_(2) को (A) के जलीय विखंडन में बुदबुदाया जाता है तो विलयन दूधिया हो जाता है। इसका उपयोग विसंक्रामक प्रकृति के कारण सफेदी में किया जाता है। A का रासायनिक सूत्र क्या होगा?
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View SolutionNaCl संरचना वाले एक ठोस AB में, 'A' परमाणु धन एकक कोष्ठिका के कोनो और फलक केंद्र पर स्थित होते है | यदि एक अक्ष के अनुदिश सभी फलक केन्द्रित पर्मानुओ को हटा दिया जाता है, तो ठोस की परिणामी रससमीकरणमिति होगी:
View Solutionनिम्नलिखित में से किस औषधि का उपयोग एक पीड़ाहारी के रूप में किया जाता है?
View Solution
