Check the following relations and for reflexivity, symmetry and transitivity: iff is divisible by (ii) iff , where and are straight lines in a plane.
Video Solution
Text Solution
The relation R is reflexive, since a is divisible by a, R is not symmetric because b is divisible by a but a is not divisible by b. i.e., aRb bRa
Again, R is transitive, since b is divisible by a and c is divisible by b, then always c is divisible by a.
|
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 1
11 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 2
10 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
Knowledge Check
In the following circuit find l1 and l2 :-
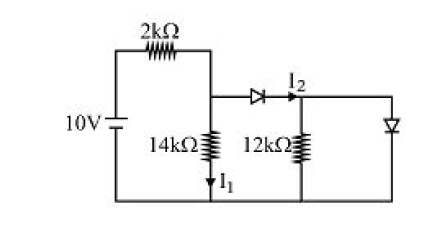 A0, 0B5 mA, 5 mAC5 mA, 0D0, 5 mA
A0, 0B5 mA, 5 mAC5 mA, 0D0, 5 mALet R be the relation over the set of all straight lines in a plane such that l1Rl2⇔l1⊥l2. Then, R is
AsymmetricBreflexiveCtransitiveDan equivalence relationIf l is the set of integers and if the relation R is defined over l by aRb, iff a - b is an even integer, a,b∈l, the relation R is
AreflexiveBanti-symmetricCsymmetricDequivalence
Straight Line L1
View SolutionLet R be the relation over the set of all straight lines in a plane such that l1 R l2⇔l1⊥l2. Then, R is (a) symmetric (b) reflexive (c) transitive (d) an equivalence relation
View SolutionLet R be a relation on the set of all lines in a plane defined by (l1, l2)∈R <=> line l1 is parallel to line l2 . Show that R is an equivalence relation.
View SolutionLet R be a relation on the set of all line in a plane defined by (l1,l2)∈Ri is parallel to line l2. Show that R is an equivalence relation.
View SolutionLet A be a relation on the set of all lines in a plane defined by (l2,l2)∈ R such that l1∣∣l2, the n R is
View Solution
