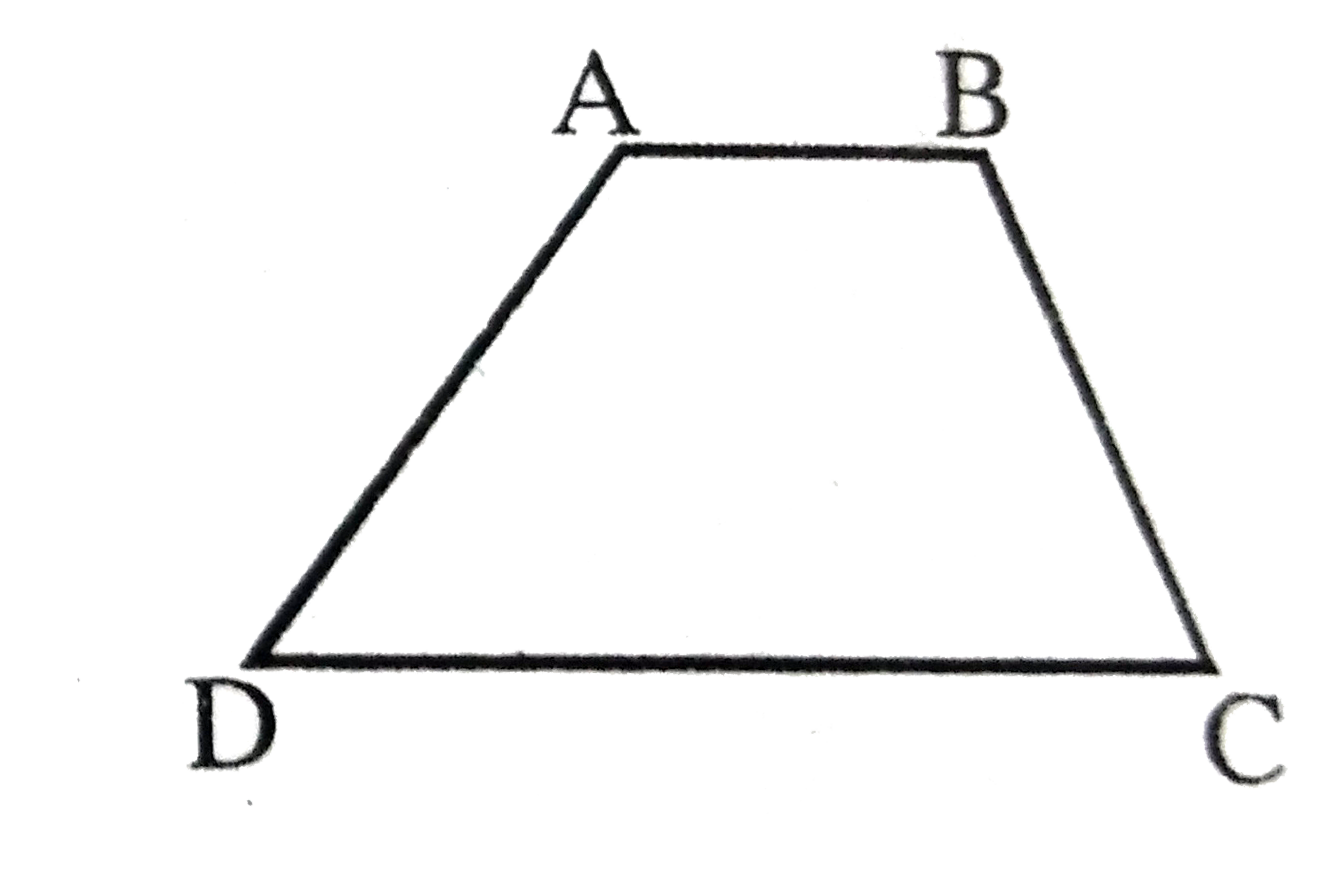
ABCD एक समलंब हैं जिसमें AB∣∣DC और AD=BC है। दर्शाइए कि
(i) ∠A=∠B
(ii) ∠C=∠D
(iii) ΔABC=ΔBAD
(iv) विकर्ण AC= विकर्ण BD है।
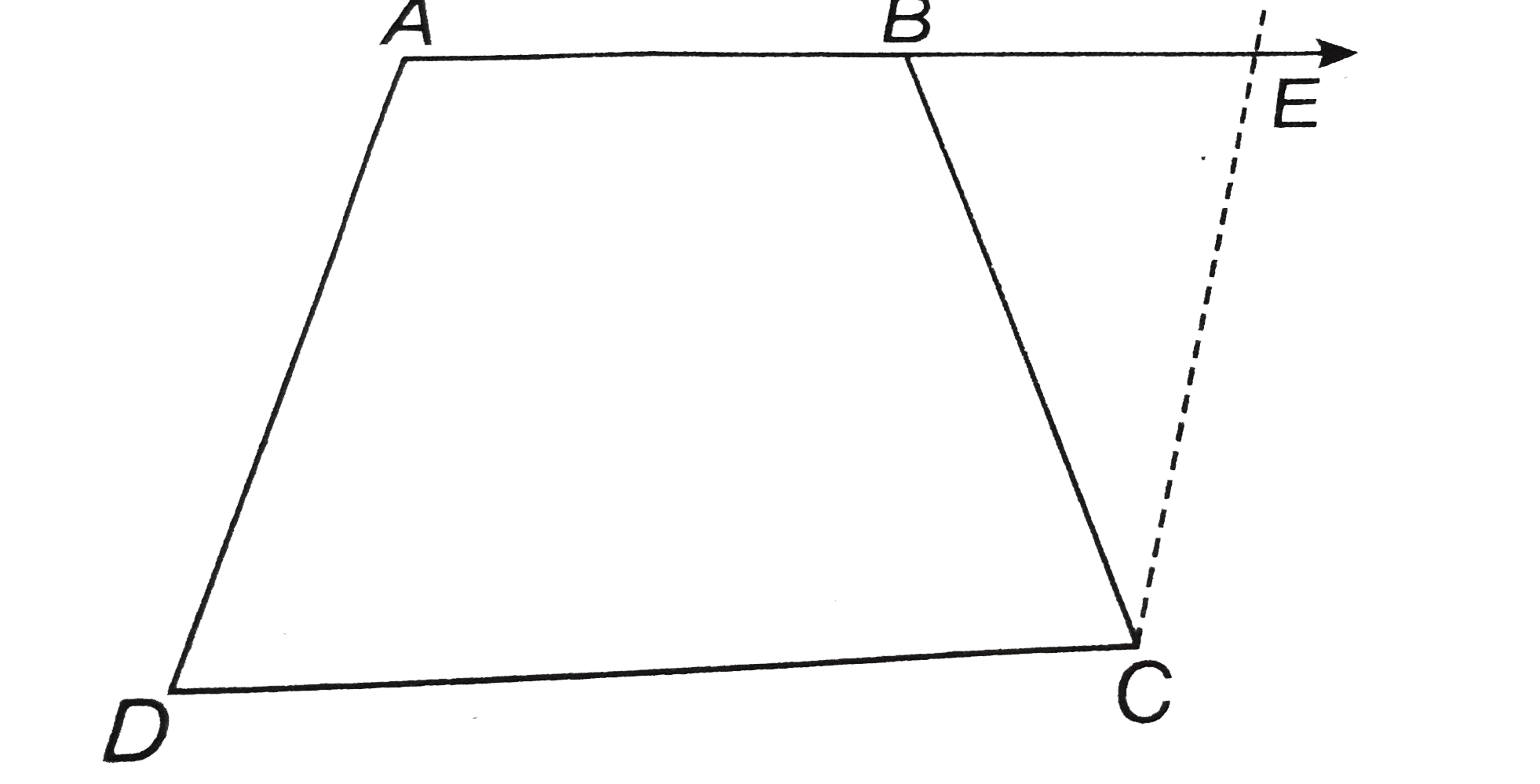
बनावटः AB को बढ़ाएं और C से होकर DA के समांतर एक रेखा खींचे जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करें।
अब चूंकि DC∣∣AE और AD∣∣CE
∴ADCE एक समांतर चतुर्भुज हुआ।
अतः AD=CE[समांतर चतुर्भुज के सम्मुख भुजाएं बराबर होती है]
DC=AE
∵AD=BC
∴BC=CE [दिया है]
अब ΔBCE में BC=CE
∴∠CBE=∠CEB [समान भुजाओं के सम्मुख कोण]
फिर ∵AD∣∣EC और तिर्यक रेखा AE उनसे मिलती है
∴∠A+∠E=180∘
या ∠A+∠CBE=180∘[∵∠E=∠CBE]
या ∠A+(180∘+∠ABC)=180∘ [रैखिक युग्म]
या ∠A−∠ABC=0
या ∠A=∠ABC
अतः ∠A=∠B………I
इस प्रकार (i) सिद्ध हो जाता है।
फिर AB∣∣DC और तिर्यक रेखा AD उनसे मिलती है।
∴∠A+∠D=180∘ [अंतः कोणों का योग]
इसी प्रकार ∠B+∠C+180∘
अतः ∠A+∠D+∠B+∠C [प्रत्येक =180∘]
लेकिन ∠A=∠B [यह (i) में सिद्ध किया जा चुका है]
∴∠D=∠C
इस प्रकार (ii) सिद्ध हो जाता है।
(iii) ΔABC और ΔBAD में
∠B=∠A [यह (i) में सिद्ध किया जा चुका है]
AB=AB [उभयनिष्ठ भुजा]
BC=AD [दिया हुआ है]
अतः ΔABC≅ΔBAD [SAS सर्वांगसमता से]
(iv) चूंकि ΔABC≅ΔBAD
∴AC=BD [CPCT]
Topper's Solved these Questions
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - अतिलघु उत्तरीय प्रश्न (समांतर चमुर्भुज, आयत, वर्ग तथा समचतुर्भुज से संबंधित परिभाषाओं, प्रमेयों तथा उपप्रमेयों के सीधे प्रयोग पर आधारित प्रश्नः)
16 Videos
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - लघु उत्तरीय प्रश्न
4 Videos
- वृत्त BOOK - KC SINHACHAPTER - वृत्त EXERCISE - वस्तुनिष्ठ प्रश्न
17 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न
7 Videos
Similar Questions
रिक्त स्थानों को भरें:
कोई समांतर चतुर्भुज एक समचतुर्भुज होगा यदि और केवल यदि उसके...................... एक-दूसरे पर लम्ब हो।
View Solutionकिसी समांतर चतुर्भुज ABCD में ∠D=110∘ तो ∠A एवं ∠B की माप अंशों में लिखें।
View Solutionवृत्त पर किन्ही दो बिन्दुओं को मिलाने वाली रेखाखंड को क्या कहते है ?
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View SolutionABCD is a trapezium in which AB∣∣CD and AD=BC. Show that
(i)∠A=∠B
(ii) ∠C=∠D
(iii) △ABC≅=△BAD
(iv) diagonal AC=diagonal BD

View SolutionABCD is a trapezium in which AB ll CD and AD=BC Show that (i) /_A=/_B (ii) /_C=/_D(iii) DeltaABC~= DeltaBAD (iv) diagonal AC=diagonal BD [Hint Extend AB and draw a line through C parallel to DA intersecting AB produced at E]
View SolutionIn the given figure,/_B
View SolutionWhich of the following symbols are not acceptable ? (i) ._(35)^(79)Br (ii) .^(79)Br (iii) ._(79)^(35)Br (iv) ._(35)Br
View SolutionIn ΔABC, ABAC=BDDC. If ∠B=70∘ and ∠C=50∘ , then ∠BAD=
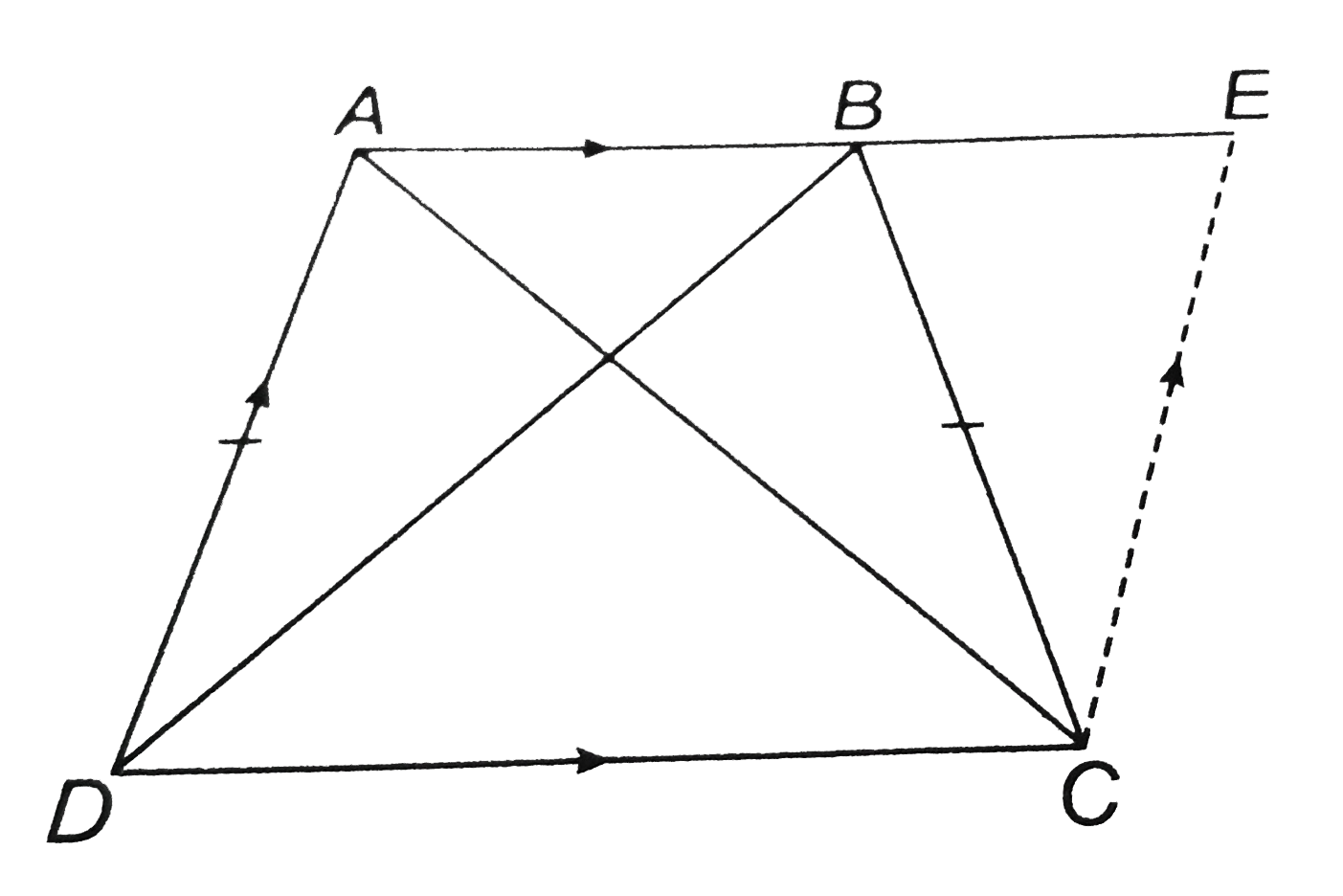
View SolutionABCD एक समलम्ब है जिसमें AB∣∣DC और AD=BC है। दर्शाइए कि:
(i) ∠A=∠B
(ii) ∠C=∠D
(iii) ΔsABC=ΔBAD
(iv) विकर्ण AC= विकर्ण BD है।
View SolutionIn quadrilateral ABCD if AB=5 cm, BC=7 cm, /_A=/_C=80^@ and /_B=/_D=100^@ then AD=?
View Solutionఏ అవయవాలు కవాటాలు కల్గి ఉంటాయి ?br i) గుండెbr ii) ధమనిbr iii) సిరలుbr iV) శోషరస నాళాలు
View Solutionవేర్ల ద్వారా శాఖీయోత్పత్తి జరిపే మొక్కbr i) డాలియాbr ii) ముల్లంగిbr iii) క్యారెట్br iv) క్యాబేజిbr
View SolutionABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D .
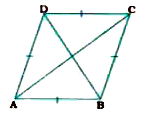
View SolutionABCD is a rhombus. Show that the diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
View Solution
