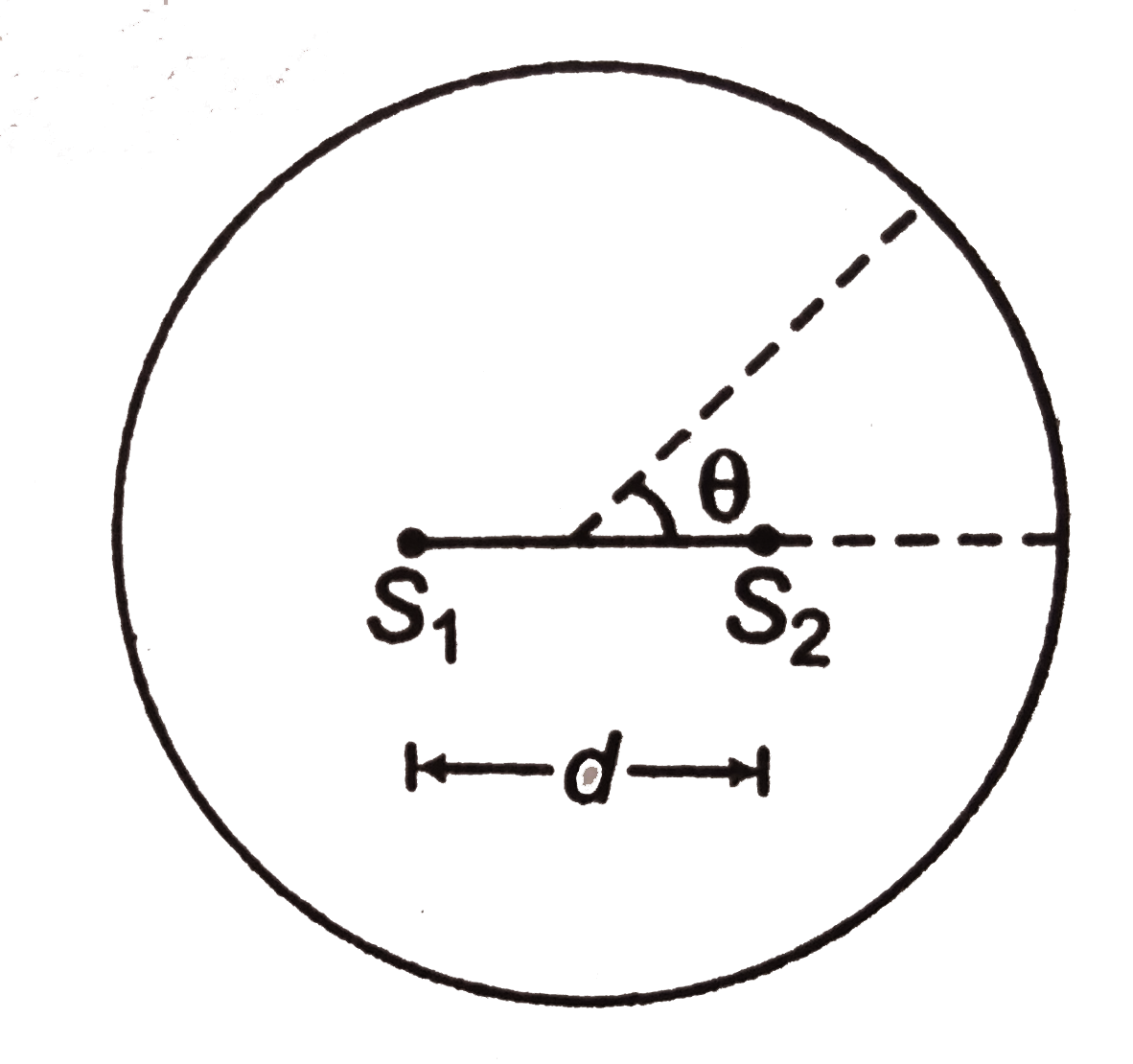
Assertion: Distance between two coherent sources S1andS2 is 4λ. A large circle is drawn around these sources with centre of circle lying at centre of S1andS2. There are total 16 maxima on this circle.
Reason: Total number of minimas on this circle are less, compared to total number of maximas.
(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b)If both Assertion and Reason are true and the Reason is not the correct explanation of the Assertion.
(c) If Assertion is true, but the Reason is false.
(d) If Assertion is false, but the Reason is true.
The correct Answer is:C
At points P and R ,
|Δx|=S1S2=4λ, therefore maxima .

At Q and S
Δx=0, therefore again maxima. Then, three
maxima in each quadrant (between P and Q or
between Q and R etc. ) corresponding to
|Δx|=λ,2λand3λ. Therefore, there are total 16 maxima.
In each quadrant there are four minima
corresponding to |Δx|=0.5λ,1.5λ,2.5λ and
3.5λ. Hence, there are total 16 minima.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1 Objective
11 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Objective question
2 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Exercise 32.2
6 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
The total number of diameters of a circle is 1 (b) 2 (c) 4 (d) uncountable number
View SolutionThere is a large circle (not a screen this time) around two coherent
sources S−1 and S2 kept at a distance d=3.4λ.
(a) Find total number of maximas on this circle.
(b) Four angular positions corresponding to third order maxima on this circle.
View Solution
Knowledge Check
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circlesAssertion: Two coherent sources S1andS2 are placed in front of a screen as shown in figure. At point P, 10th order maxima is obtained. Then , 11th order maxima will be obtained above P.

Reason: For 11th order maxima path difference should be more.A(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.B(b)If both Assertion and Reason are true and the Reason is not the correct explanation of the Assertion.C(c) If Assertion is true, but the Reason is false.D(d) If Assertion is false, but the Reason is true.Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 Astraigth linesBsemi-circleCconcentric circlesDpoints
Astraigth linesBsemi-circleCconcentric circlesDpoints
ln n(n≥3) circles the centres of no three circles are collinear. If the number of the radical axes of the circles is equal to the number of the radical centres of the circles then n2−4n−5=
View SolutionLet there be n circles no three of which have collinear centres. If the total number of radical axes is equal to total number of possible radical centres, then possible value of n is
View SolutionTwo coherent light sources A and B with separation 2λ or placed on the x-axis symmetrically about the origin. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and centre at the origin.
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionTwo coherent light sources S1 and S2(λ=6000Å) are 1mm apart from each other. The screen is placed at a distance of 25cm from the sources. The width of the fringes on the screen should be
View Solution
