A lens with a focal length of 16cm produces a sharp image of an object in two positions, which are 60cm apart. Find the distance from the object to the screen.
The correct Answer is:A, C
f=d2−x24d (displacement method)
f=16cm,x=60cm
Substituting the values we get,
d=100cm
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Single Correct
41 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions
1 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
(a) A screen is kept at a distance of 1m from the object. A converging lens between the object and the screen, when placed at any of the two positions which are 60cm apart, forms a sharp image of the object on the screen. Find the focal length of the lens.
(b) In the two positions of the lens, lateral size of the image is 4cm and 9cm. Find the size of the object.
View SolutionA thin converging lens with focal length f=25cm projects the image of an object on a screen removed from the lens by a distance l==5.0m. Then the screen was draws closer to the lens by a distance Δl=18cm. By what distance should the object be shifted for its image to become sharp again ?
View Solution
Knowledge Check
A thin converging lens of focal length f = 25 cm forms the image of an object on a screen placed at a distance of 75 cm from the lens. Now the screen in moved closer to the lens by a distance of 25 cm. The distance through which the object has to be shifted so that its image on the screen is sharp again is
A37.5 cmB16.25 cmC12.5 cmD13.5 cmA convex lens of focal length 30 cm produces 5 times magnified real image of an object. What is the object distance?
A36cmB25cmC30cmD150cmA thin biconvex lens of focal length f=25cm forms a real image of a real object an a screen. The object is separated by 5cm from the lens. The screen is drawn closer to the lens by a distance 18cm. Through what distance (approximately) must the object be shifted so that its image is again formed on the screen ?
A0.5mm toward leftB0.25mm toward leftC2.5mm toward leftD1.4mm toward left
An object is placed at a certain distance from a screen. A convex lens of focal length 20cm is placed between the screen and the object. A real image is formed on the screen for two positions of the lens, which differ by a distance of 10cm. What is the distance of the object from the screen ?
View SolutionA convex lens is coaxially placed with a concave lens. A screen is placed at a distance of 100 cm apart from the combination. The focal length of convex lens is 15 cm. Determine the focal length of the concave lens if image of object placed at a distance of 20 cm, from the combination, is projected on the scrcen.
View SolutionDetermine the position of the image produced by an optical system consisting of a concave mirror with a focal length of 10cm and a convergent lens with a focal length of 20cm. The distance from the mirror to the lens is 30cm and from the lens to the object is 40cm. Consider only two steps. Plot the image.
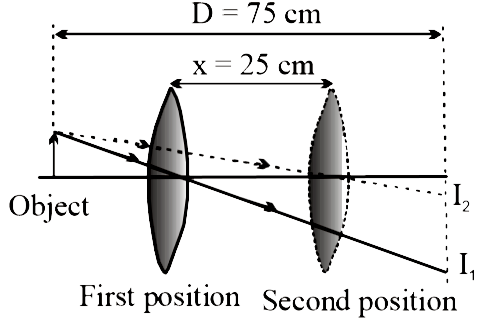
View SolutionA convex lens when placed in the first position forms a real image of an object on a fixed screen. The distance between the object and the screen is 75 cm. On displacing the lens from first position by 25 cm to the second position, again a real image is formed on the screen. Then the focal length of the lens is
View SolutionThe focal length of convex lens is 20 cm. If an object of height 4 cm is placed at a distance of 30 cm from the lens, find:
The position of the image
View Solution
