A constant current I flows through a long straight wire as shown in figure. A square loop starts moving towards righ with as constant speed v.

a Find induced emf produced i the loop as a function x
b. If total resistance of the loop is R, then find induced current in the loop,
Method 1
a. Using the result of magnetic flux obtained in example 1, we have
ϕB=μ0IC2πIn(a+bc)
Here a=x,b=c=a
substituting the values, we get
ϕB−μ0Ia2πln(x+ax)
=μ0Ia2πln(1+ax)
Now, |e|=∣∣∣dϕBdt∣∣∣=μ0Ia2π(xx+a)(ax2)dxdt
Putting dxdt=v, we have
|e|=μ0Ia22πx(x+a)v
b. induced curent
I∈=|e|R=μ0Ia2v2πRx(x+a)
Method 2
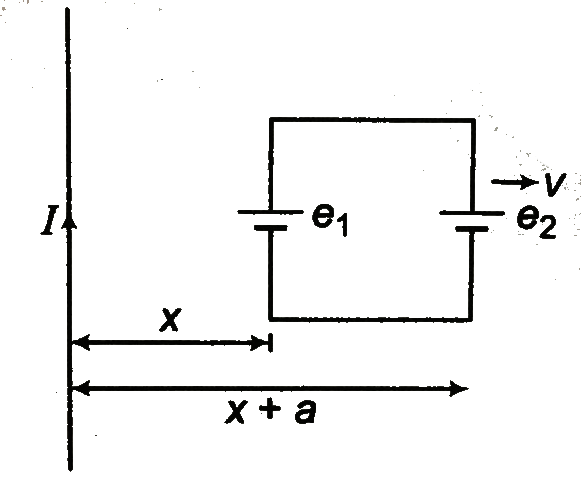
e1=B1vl=μ02πIxva
e2=B2vl=μ02πIx+ava
e1>e2
enet=e1−e2=μ0Iva2π(1x−1x+a)
=μ0Iva22πx(x+a)
This is the name result as was obtained in method 1.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 2
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 3
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Current in a long current carrying wire is I=2t
A conducting loop is placed to the right of this wire. Find
a. magnetic flux ϕB passing through the loop.
b. induced emf|e| prodced in the loop.
c. if total resistance of the loop is R, then find induced current Iin in the loop.
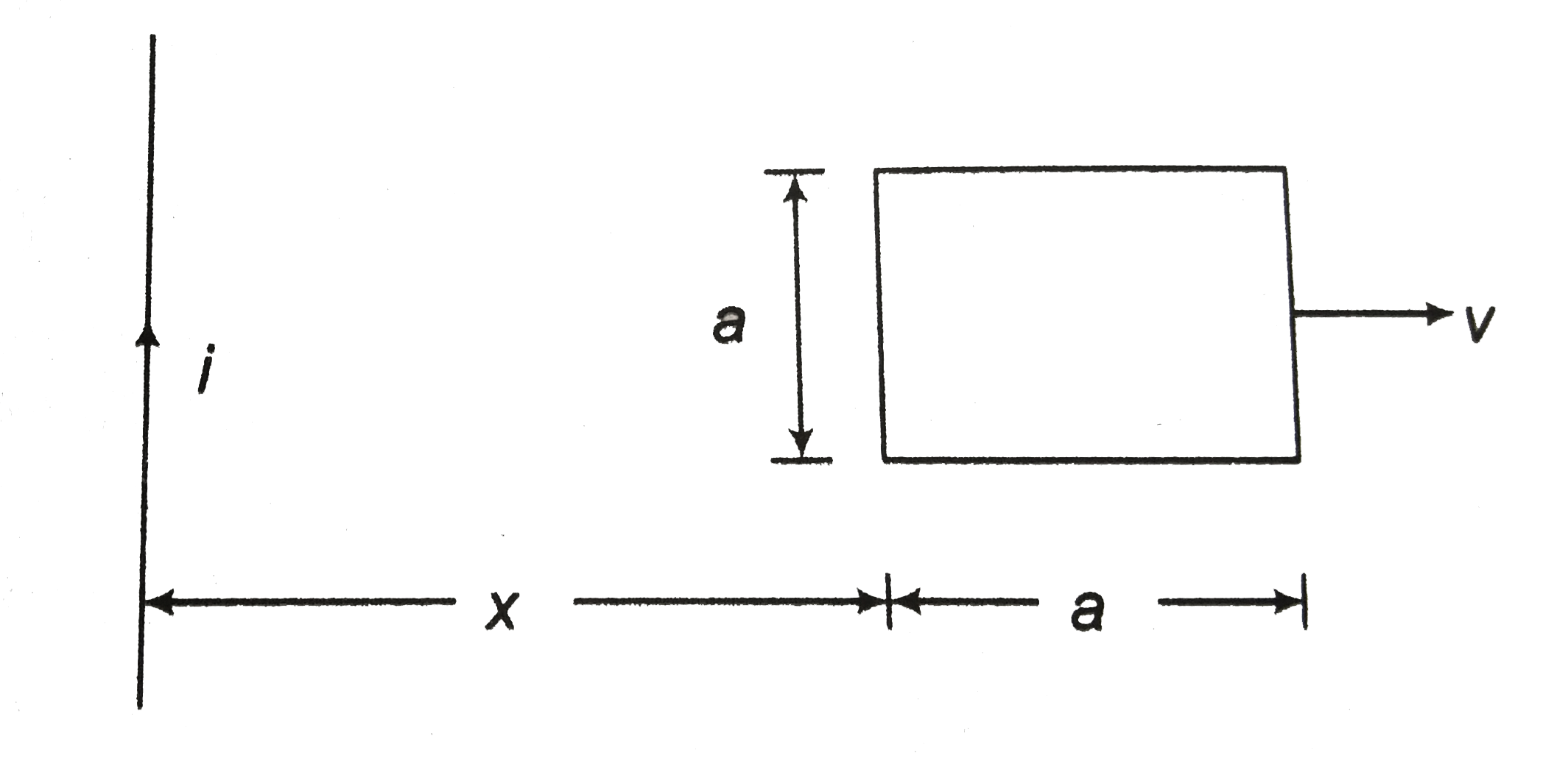
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
View Solution
Knowledge Check
When a loop moves towards a stationary magnet with speed v, the induced emf in the loop is E. If the magnet also moves away from the lop with the same speed, then the emf inducted in the loop is
AEB2ECE2DzeroA loop and an infinite wire are placed side by side as shown in the figure. If the current I in the wire is increased then the induced current in the loop is
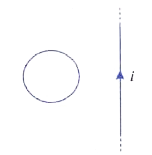 AclockwiseBanticlockwiseCzeroDcannot determine
AclockwiseBanticlockwiseCzeroDcannot determineThe current flows from A to B as shown in the figure The direction of the induced current in the loop is :
 AclockwiseBanticlockwiseCstraight lineDnone of these
AclockwiseBanticlockwiseCstraight lineDnone of these
A conducting loop is being pulled with speed v from region I of magnetic field to region II. If resistance of the loop is R, current induced in the loop at the instant shown is
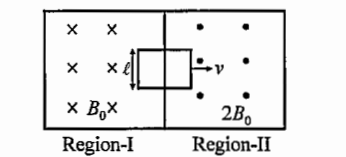
View SolutionA rectangular loop is placed adjacent toa current carrying straight wire as shown in Figure. If the loop is rotated about an axis passing through one of its sides find the direction of induced current in the loop.

View SolutionFig. 6.15 shows a current carrying solenoid moving towards a conducting loop. Find the direction of the current induced in the loop.

View SolutionA rectangular loop is placed near a current carrying straight wire as shown in the figure. If the loop is rotated about an axis passing throught one of its sides find the direction of induced current in the loop.
View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

View Solution
