Uniform electrilcf and magnetic fields with strength E and B are directed along of x-axis. A particle with specific charge qm leves the origin in the direction of x-axis with an initial velocity v0. Find
a. the y-coordinate of the particle when it crosses the y-xis for nth time.
b. the angle α between the particle's velocity vector adn the y-axis for nth time
a. As discussed in type 9 path of the particle is a helix of incresing pitch. The axis of the helix is parallel to y-axis (parrallell to E) nd plane of circle of the helix is xz (perendicular to B). The particle will cross the y-axis after time.
t=hT−n(2πmBq)=2πmnBq
The y-coordinate of particle at this instant is
y=12ayt2
ay=Fym=qEm
∴y=12(qEm)(2πmnBq)2
=2n2mEπ2qB2
At this moment y-component of its velocity is
vy=ayt=(qEm)(2πmnBq)=2πn(EB)
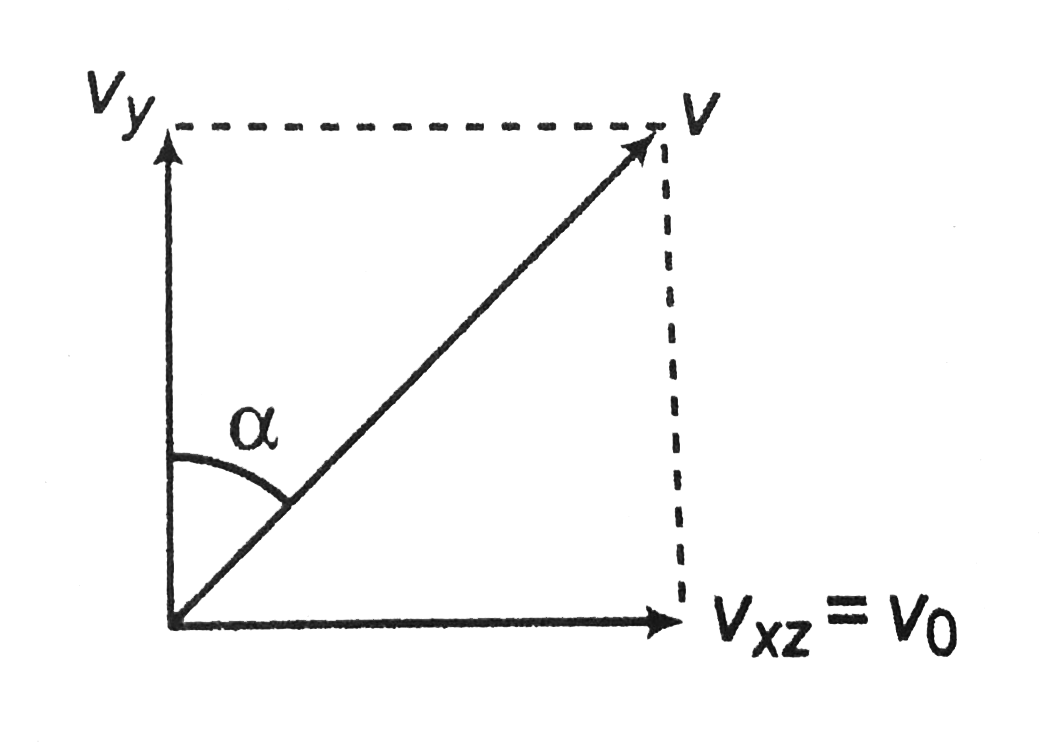
α=tan−1(vxzv−y)
Here,vxz=√v2x+v22=v0
orα=tan−1(Bv02πnE)
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:Exercise
Explore 160 Videos
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEYChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
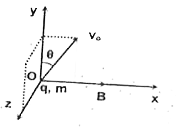
Unifrom electric and magnetic fields with strength E and induction B respectively are directed along the y axis (Fig). A particle with specific charge q/m leaves the origin O in the direction of the z axis with an initial non-realtive velocity v0 find:
(a) the coordinate yn of the particle when it crossses then y axis for the nth time,
(b) the angle α between the particle's velocity vector and the y axis at that moment.

View SolutionUniform electric field E and magnetic field B, respectively, are along y-axis as shown in the figure. A particle with specific charge q/m leaves the origin O in the direction of x-axis with an initial non-relativistic speed v0.

The angle α between the particle’s velocity vector and y-axis at that moment is:
View Solution
Knowledge Check
Uniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The coordinate y_nofthepartic≤whenitcrossesthey−aξsforthen^(th) time isA2π2mn2EqB2Bπ2mn2EqB2C2π2mn2E3qB2D√3π2mn2EqB2Uniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The angle α between the particle's velocity vector and y-axis at and moment isAtan−1(3v0B2πnE)Btan−1(v0BπnE)Ctan−1(v0B√2πnE)Dtan−1(v0B2πnE)A charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
Amv0qBB2mv0qBCmv02qBDNone of these
A particle of mass m and charge q is lying at the origin in a uniform magnetic field B directed along x-axis. At time t = 0, it is given a velocity v0, at an angleθ with the y-axis in the xy-plane. Find the coordinates of the particle after one revolution.
View SolutionA positively charged particle with specific charge σ leaves the origin with a velocity u directed along positive x direction. The entire space has a uniform electric field (E) and magnetic field (B) directed along the positive y direction. Find the angle that the velocity of the particle makes with y direction at the instant it crosses the y axis for nth time.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionThere exist uniform magnetic and electric fields of magnitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionA particle of mass m, carrying a charge q, is lying at the origin in a uniform magentic field directed along X axis. At the instant t = 0 it is given a velocity va at an angle θ with the y-axis, in the XY plane. The coordinates of the particle after two revolution will be
View Solution

