A uniform circular hoop of string is rotating clockwise in the absence of gravity. The tangential speed is $v_{0}$ . Find the speed of the wave travelling on this string.

Video Solution

Text Solution

Verified by Experts

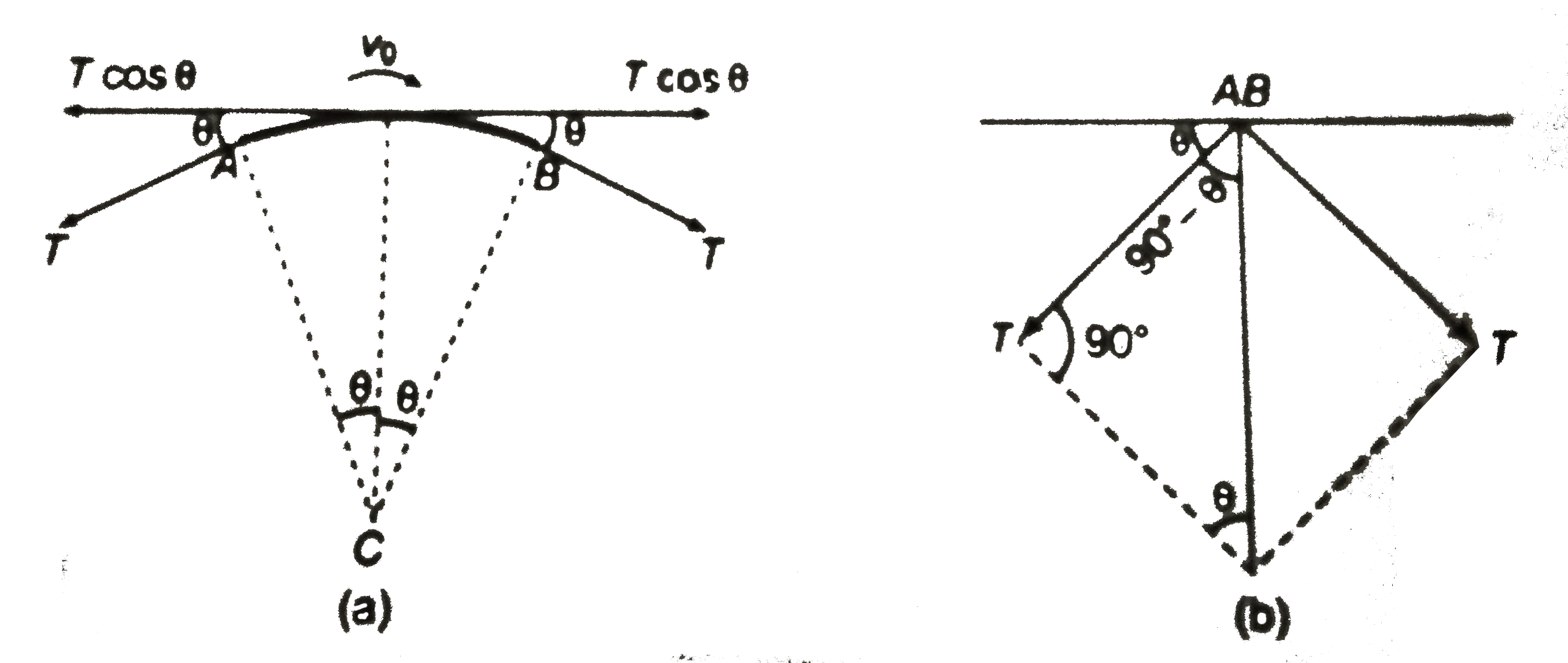
Let $T$ be the tension in the string. Consider a small circular element $A B$ of the string of length,
$Δ l = R (2 θ)$ (R =radius of hoop)
The components of tension $T cos θ$ are equal and opposite and thus cancel out. The cpmponents towards centre $C$ (i.e. $T sin θ$ ) provides the necessary force to elemment $A B$ .
$∴ 2 T sin θ = \frac{m v_{0}^{2}}{R}$ ...(i)
Here, $m = μ Δ l = 2 μ R θ$ $(μ = \frac{mass}{length})$
As $θ$ is small, $sin θ \approx θ$
Substituting in Eq. (i), we get
$2 T θ = \frac{2 μ R θ v_{0}^{2}}{R}$
or $\frac{T}{μ} = v_{0}^{2}$
or $\sqrt{\frac{T}{μ}} = v_{0}$ ...(ii)
Speed of wavw travelling on this string,
$v = \sqrt{\frac{T}{μ}} = v_{0}$ [from Eq. $(i i)$ ]
i.e. the velocity of the transverse wave along the hoop of string is the same as the velocity of rotation of the hoop, viz. $v_{0}$ .

Updated on:21/07/2023

The speed of transverse wave on a stretched string is
Adirectly proportional to the tension in the string
Bdirectly proportional to the square root of the tension
Cinversely proportional to live
Dinversely proportional to square of tension
A string of length 2L, obeying Hooke's Law, is stretched so that its extension is L. The speed of the tranverse wave travelling on the string is v. if the string is futher stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
A $\sqrt{2}$ V
BV
C $2 \sqrt{2} V$
D2V
A uniform string of length 20 m & mass 1 kg is hung vertically. Find the speed of wave at the mid point of the string :
A $20 m / s$
B $30 m / s$
C $10 \sqrt{2} m / s$
D $10 m / s$