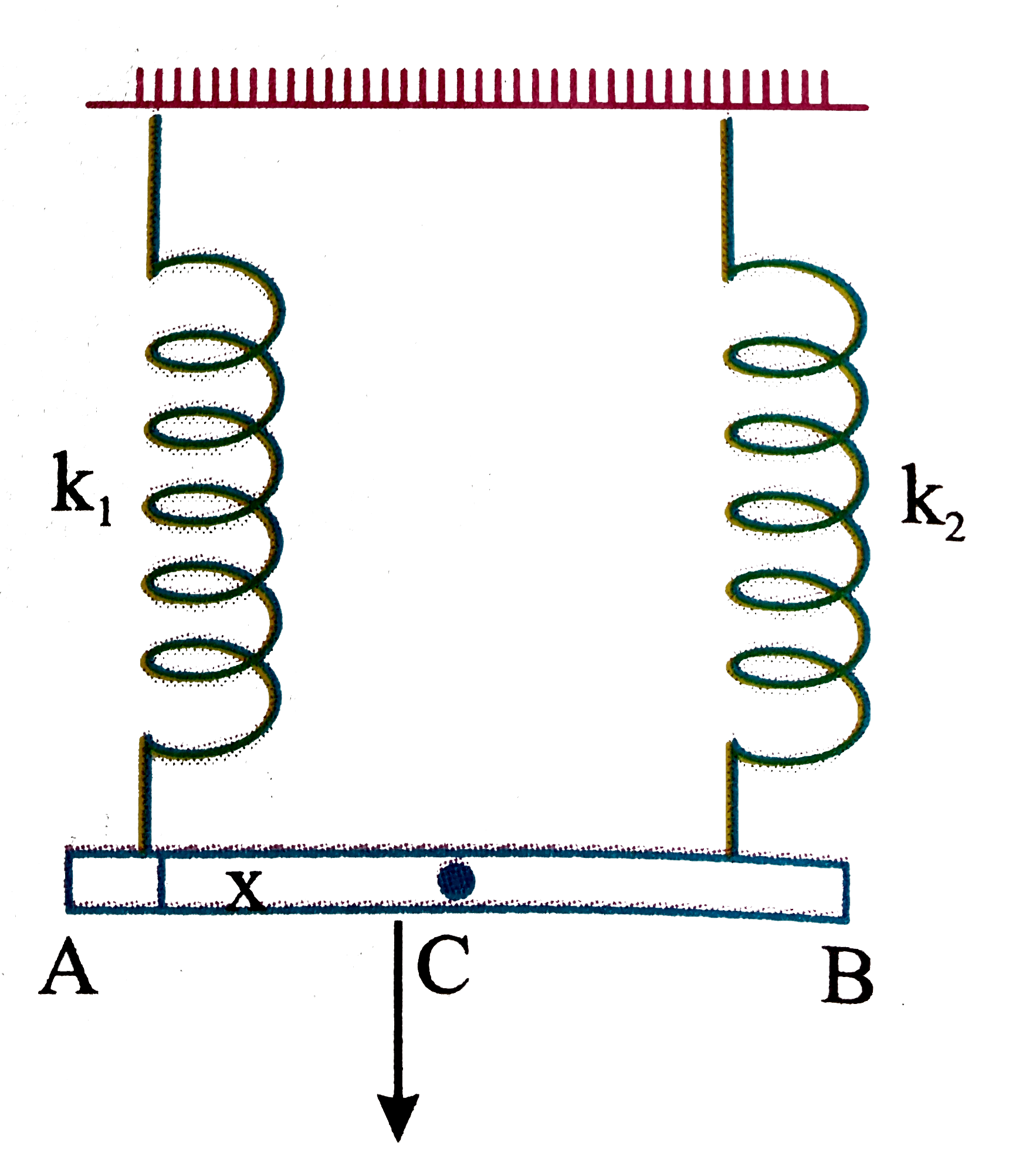
Two light vertical springs with equal natural length and spring constants k1 and k2 are separated by a distance l. Their upper end the ends A and B of a light horizontal rod AB. A vertical downwards force F is applied at point C on the rod. AB will remain horizontal in equilibrium if the distance AC is
lk1k2
lk1k2+k1
lk2k1
lk2k1+k2
The correct Answer is:D
∑(Moments aboutC)=0
∴(k1x)AC=(k2x)BC
∴ACBC=k2k1….(i)
AC+BC=l….(ii)
Soving these two equation we get,
AC=(k1k1+k2)l
Similar Questions
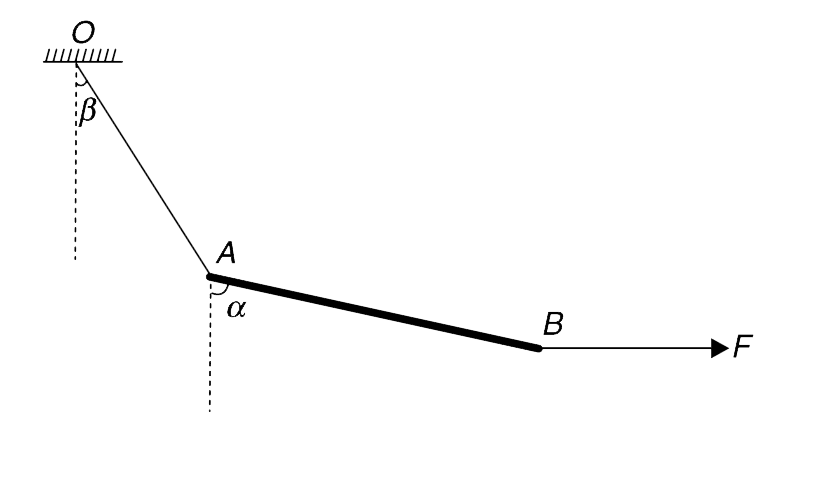
A stick AB of mass M is tied at one end to a light string OA. A horizontal force F=Mg is applied at end B of the stick and its remains in equilibrium in position shown. Calculate angles α and β.
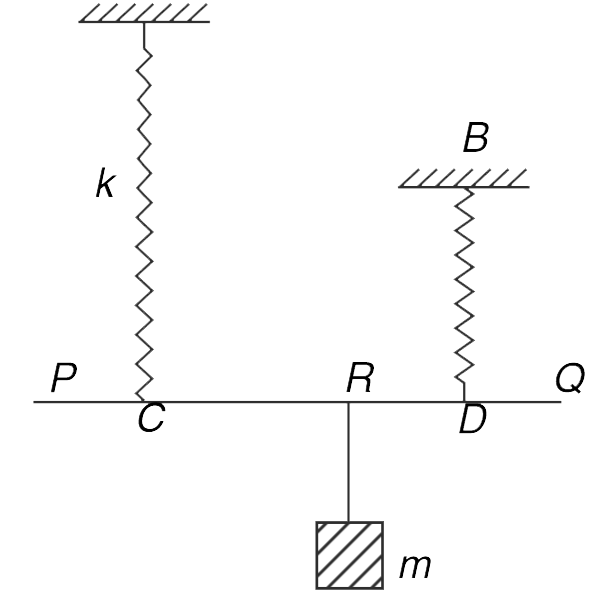
View SolutionTwo ideal springs of same make (the springs differ in their lengths only) have been suspended from points A and B such that their free ends C and D are at same horizontal level. A massless rod PQ is attached to the ends of the springs. A block of mass m is attached to the rod at point R. The rod remains horizontal in equilibrium. Now the block is pulled down and released. It performs vertical oscillations with time period T=2π√m3k where k is the force constant of the longer spring.
(a) Find the ratio of length RC and RD.
(b) Find the difference in heights of point A and B if it is given that natural length of spring BD is L.
View Solution
Knowledge Check
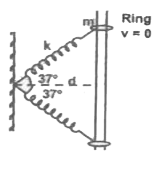
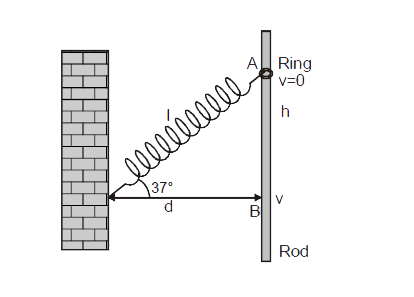
One end a light spring of natural length d and spring constant k(=mg/d) is fixed on a rigid support and the other end is fixed to a smoth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the support. Initially , the spring makes an angle of 37∘ with the horizontal as shown in the figure. The system is released from rest. The speed of the ring at the same angle subtended downward will be
 A√2gdB√3gdC√4gdD√gd/2
A√2gdB√3gdC√4gdD√gd/2A uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
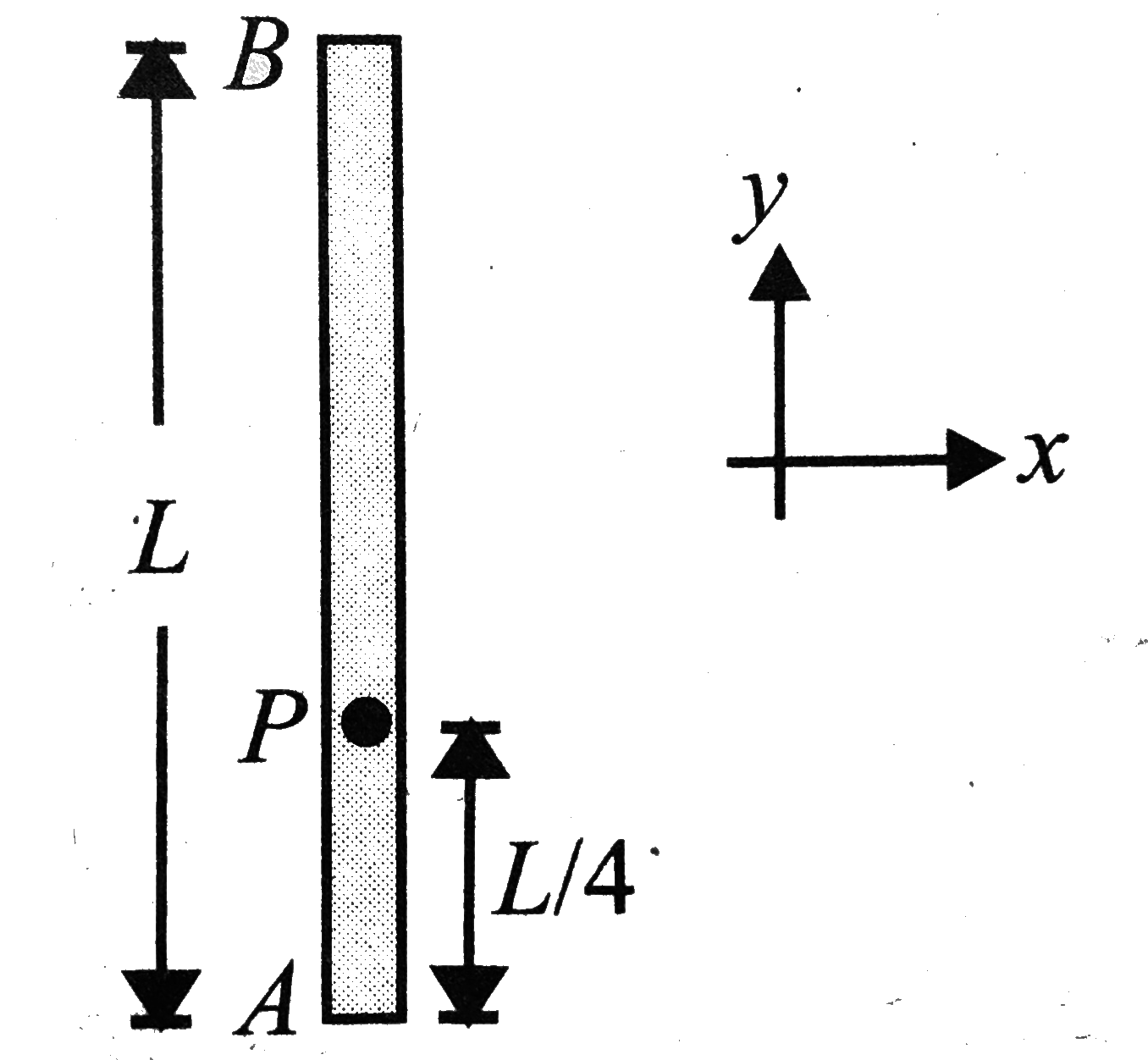
The acceleration of end B of the rod isA−6g7ˆi−12g7ˆjB−5g7ˆi−6g7ˆjC−18g7ˆi−5g7ˆjD−18g7ˆi−9g7ˆjTwo light verticle springs 1 and 2 of stiffness K and 2K are connected by a 1 light horizontal rod. A bead of chewing gum of mass 'm' is placed gently at the mid point of the rod and lowered slowly.
The ratio of magnitude of work done by the external agent to that by gravity in lowering the bead till it remains at rest isA1:1B1:2C2:1D1:4
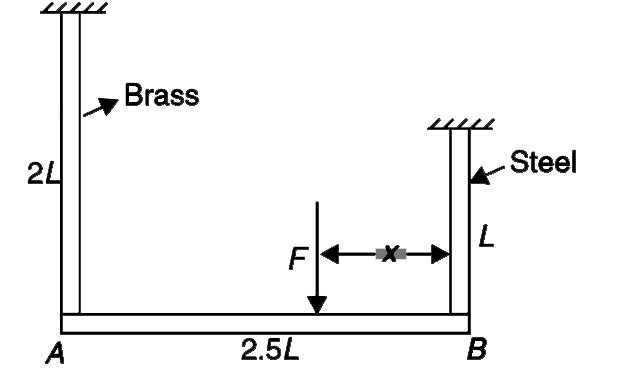
A very stiff bar (AB) of negligible mass is suspended horizontally by two vertical rods as shown in figure. Length of the bar is 2.5 L. The steel rod has length L and cross sectional radius of r and the brass rod has length 2L and cross sectional radius of 2r . A vertically downward force F is applied to the bar at a distance x from the steel rod and the bar remains horizontal. Find the value of x if it is given that ratio of Young’s modulus of steel and brass is YsYB=2.
View SolutionOne end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
View Solutiontwo light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
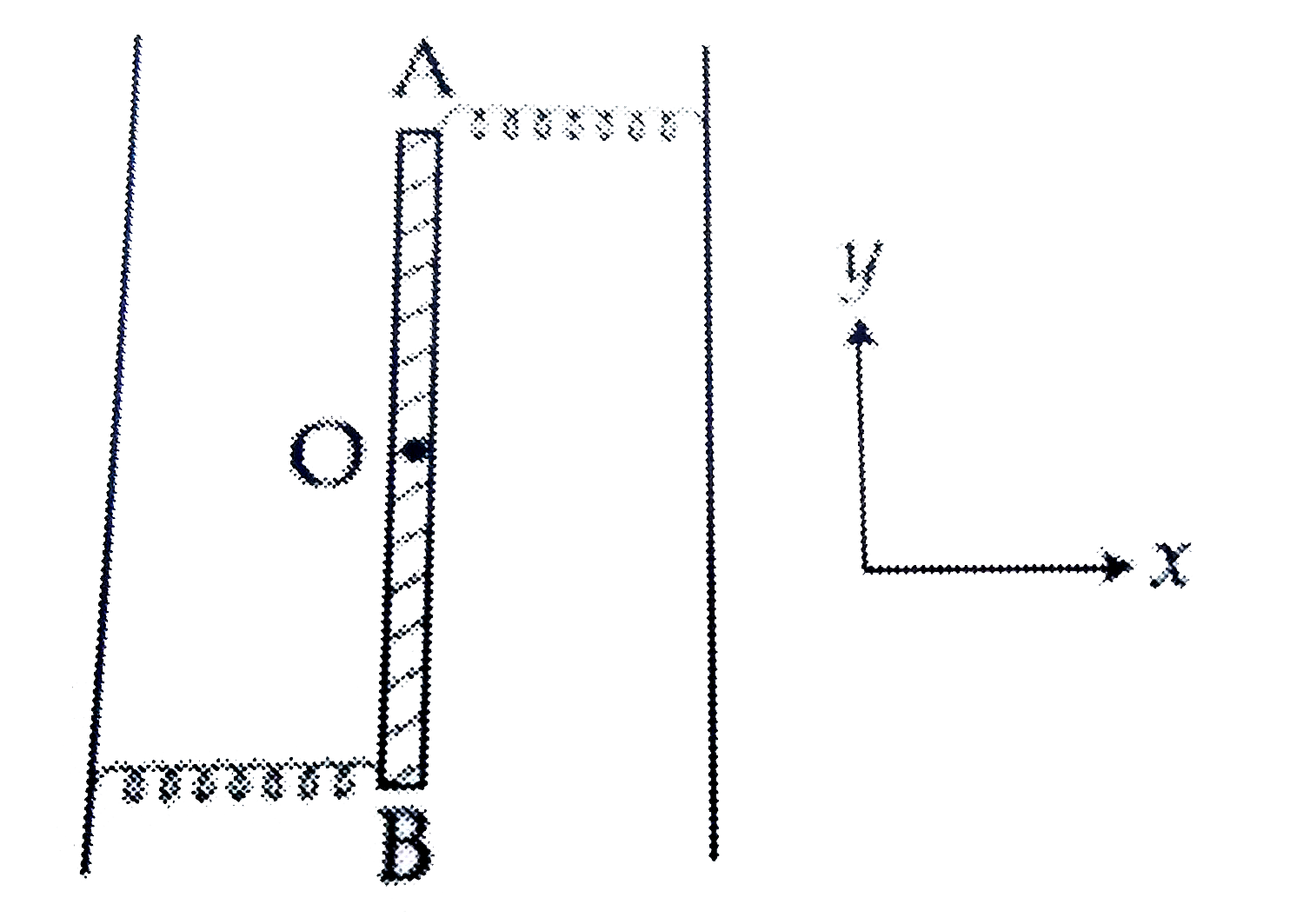
View Solution
A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionTwo light vertical springs 1 and 2 of stifiness k and 2k are connected to a light horizontal rod at its two ends as shown. A bead of chewing gam of mass 'm' is sticked gently at the mid point of the rod and lowcred slowly, such that where equilibrium is reached the bead displaced by x0. The period of SHM of the bead is 2π√pnqK, Find |p−q|.
'(##CEN_KSR_PHY_JEE_C16_E01_032_Q16##)'
View Solution
