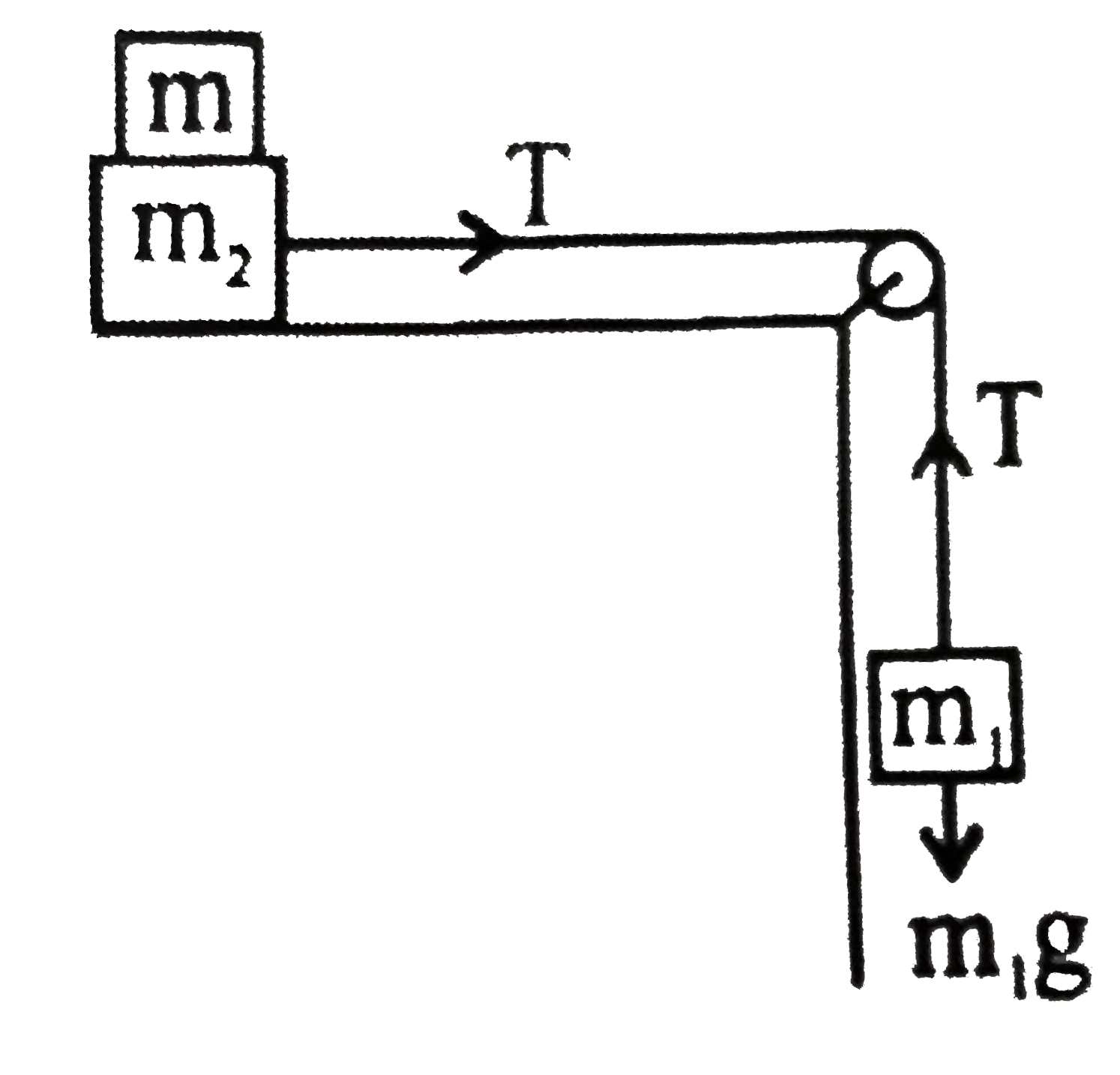
Two masses $m_{1} = 10 K g$ and $m_{2} = 5 k g$ are connected by an ideal string as shown in the figure. The coefficient of friction between $m_{1}$ and the surface is $μ = 0.2$ Assuming that the system is released from rest calculate the velocity of blocks when $m_{2} h a s d e s c e n d e d b y$ 4m $.$ (g=10 m//s^(2))
.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$v_{m_{1}} = v_{m_{2}}$
$d_{m_{1}} = h_{m_{2}} = 4 m$
Using the equation,
$E_{i} - E_{f} =$
Work done against friction
$0 - [\frac{1}{2} \times (10 + 5) (v^{2}) - 5 \times 10 \times 4]$
$= 0.2 \times 10 \times 10 \times 4$
Solving we get,
$v = 4 m / s$

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Knowledge Check

Two blocks of masses $M_{1} = 4$ kg and $M_{2} = 6 k g$ are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block $M_{1}$ and the horizontal surface is 0.4. when the system is released, the masses $M_{1}$ and $M_{2}$ start accelrating. What additional mass m should be placed over $M_{1}$ so that the masses $(M_{1} + m)$ slide with a uniform speed?

A12 kg
B11 kg
C10 kg
Dkg
Two blocks A and B of mass 10 kg and 20 kg respectively are placed as shown in figure .Coefficient of friction between all the surface is 0.2 $(g = 10 m / s^{2})$ Then,

ATension in the string is 306 N
BTension in the sr=tring is 132 N
Caccelerration of block B is $2.6 m / s^{2}$
Dasseleration of block B is $4.7 m / s^{2}$
Two moasses $m_{1} = 5 k g and m_{2} = 10 k g,$ connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is $0.15 .$ The minimum weitght m that should be put on top of $m_{2}$ to stop the motion is :-

A $27.3 k g$
B $43.3 k g$
C $10.3 k g$
D $18.3 k g$

Recommended Questions

Home
Ask Doubt
Profile