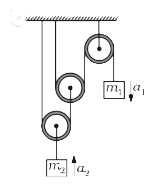
Make the constraint relation between a1,a2 and a3
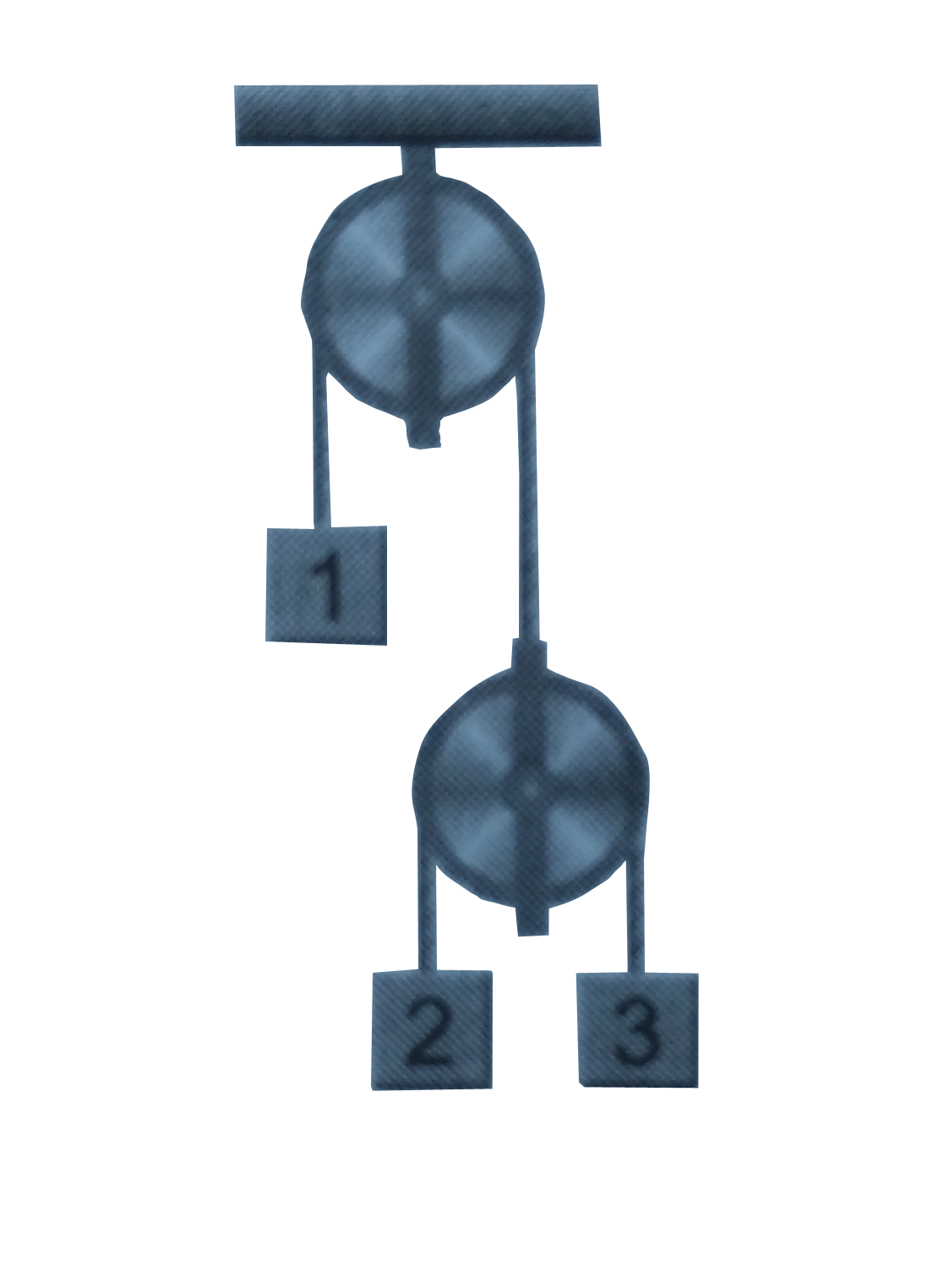
Point 1,2,3 and 4 are movable .Let that displacement , from the fixed dotted line bex1,x2,x3 and x4(ignoring the length over the pulley)

We have,
x1+x4=l1 (length of first string)
and (x2−x4)+(x3−x4)=l2 (length of second string)
or x2−x3−2x4)=l2 ...(ii)
On double different with respect to time, we get
a1+a4=0...(iii)
and a2+a3−2a4=0 ...(iv)
but a4=−a1 [From Eq. (iii)]
We have a2+a3+2a1=0
This is the required constraint relation between a1,a2 anda3
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.4
3 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.5
2 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.2
9 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
The line that joins the saturn to the sun sweeps area A1,A2 and A3 in time intervals of 6 weeks, 3 weeks and 2 weeks respectively as shows in the Fig. What is the correct relation between A1,A2 and A3?
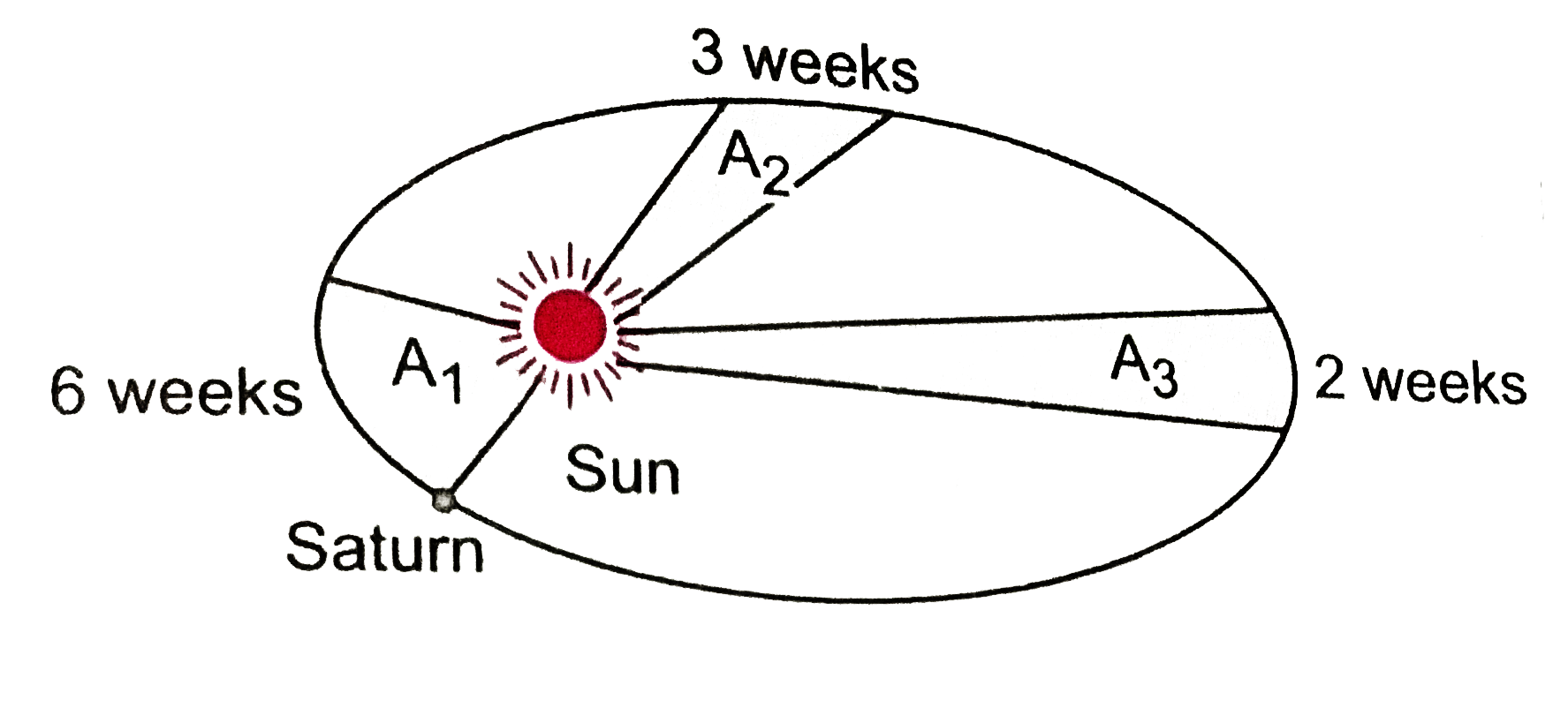
View SolutionThe line that joins the saturn to the sun sweeps area A1,A2 and A3 in time intervals of 6 weeks, 3 weeks and 2 weeks respectively as shows in the Fig. What is the correct relation between A1,A2 and A3?

View Solution
Knowledge Check
If the blocks are moving as shown in the figure the relation between a1 , a2 and a3 will be.
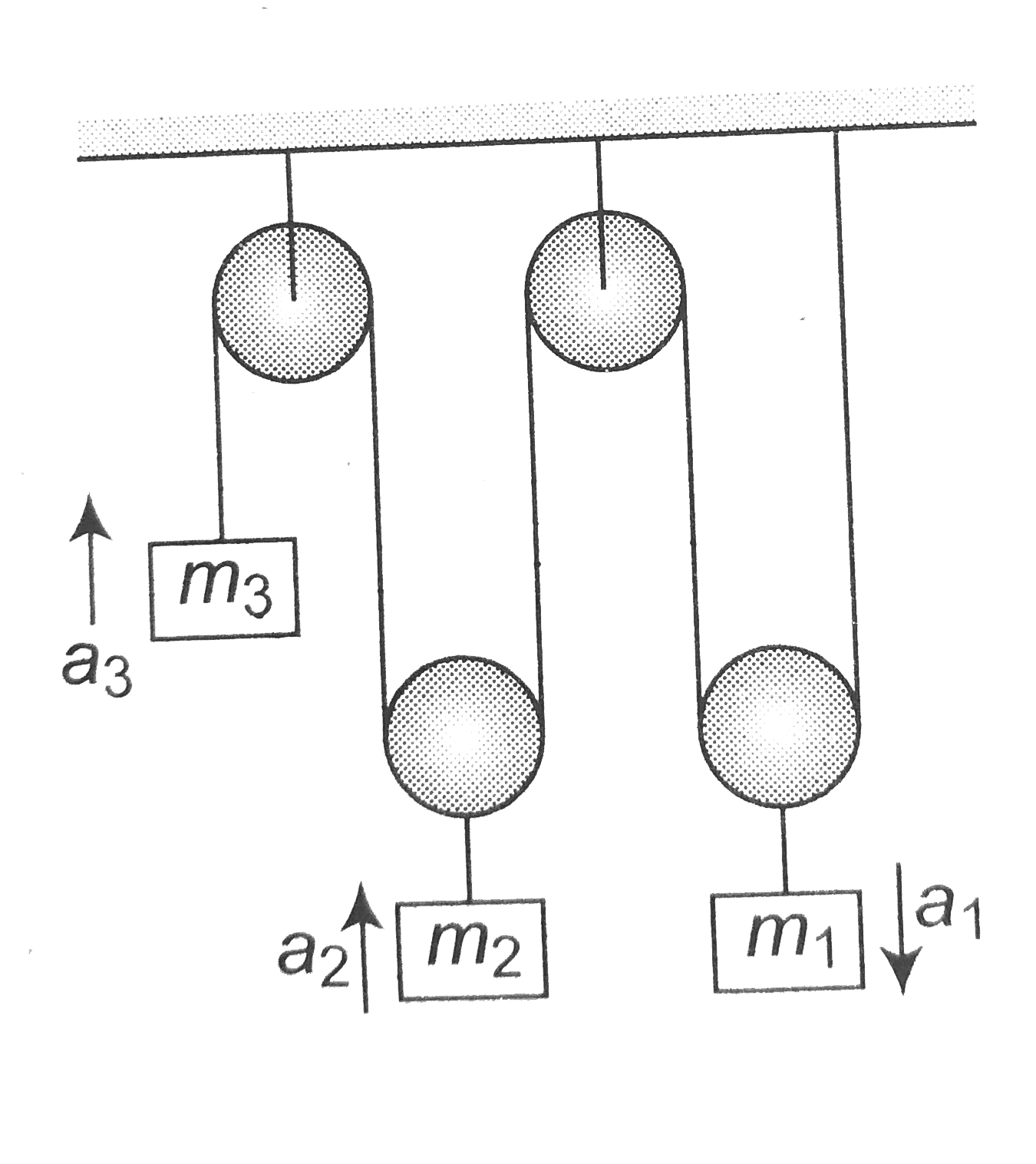 A2a1+2a2+a3=0B2a1−2a2+a3=0C2a1−2a2+2a3=0D2a2−2a1+a3=0
A2a1+2a2+a3=0B2a1−2a2+a3=0C2a1−2a2+2a3=0D2a2−2a1+a3=0A pulley-block arrangement is shown in the adjacent figure, if acceleration of m1,m2 and m3 are a1,a2 and a3 respectively, then relation between a1,a2 and a3 is ( All string and pulleys are ideal . )
 Aa2−a3+10a1=0Ba3−a2+10a1=0Ca2−2a3+10a1=0D2a2+a3+5a1=0
Aa2−a3+10a1=0Ba3−a2+10a1=0Ca2−2a3+10a1=0D2a2+a3+5a1=0In the adjacent figure, all the pulleys are frictioniess and massless, all the stringes are also massless. The relation between a1,a2 and a3 is (where a1,a2 and a3 are the acceleration of masses m1,m2 and m3 respectively in the direction as shown in the figure)
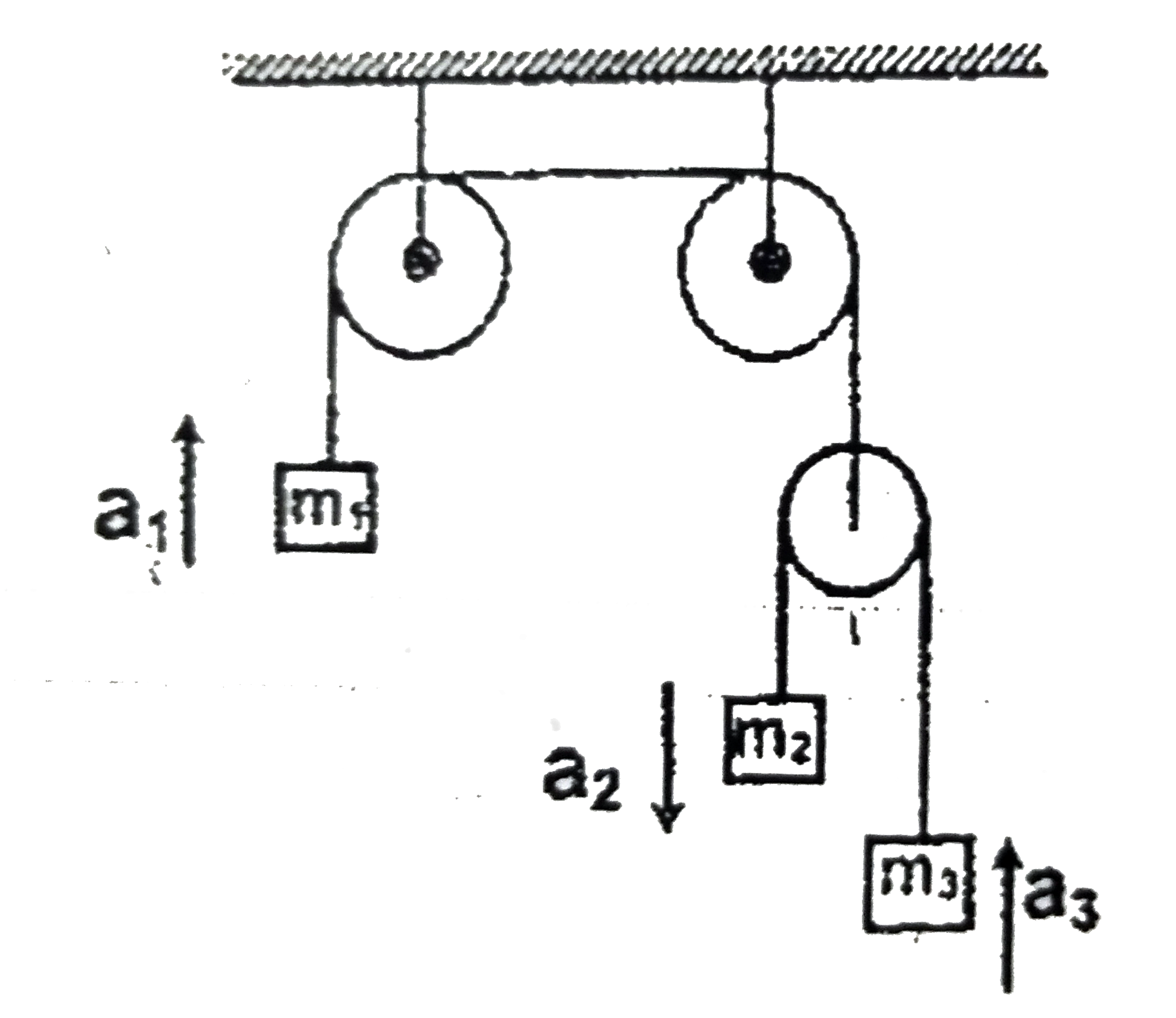 Aa3−a2+2a1=0Ba3+a2−2a1=0C2a2+a3=2n1DNone of these
Aa3−a2+2a1=0Ba3+a2−2a1=0C2a2+a3=2n1DNone of these
Find the relation between a1 and a2
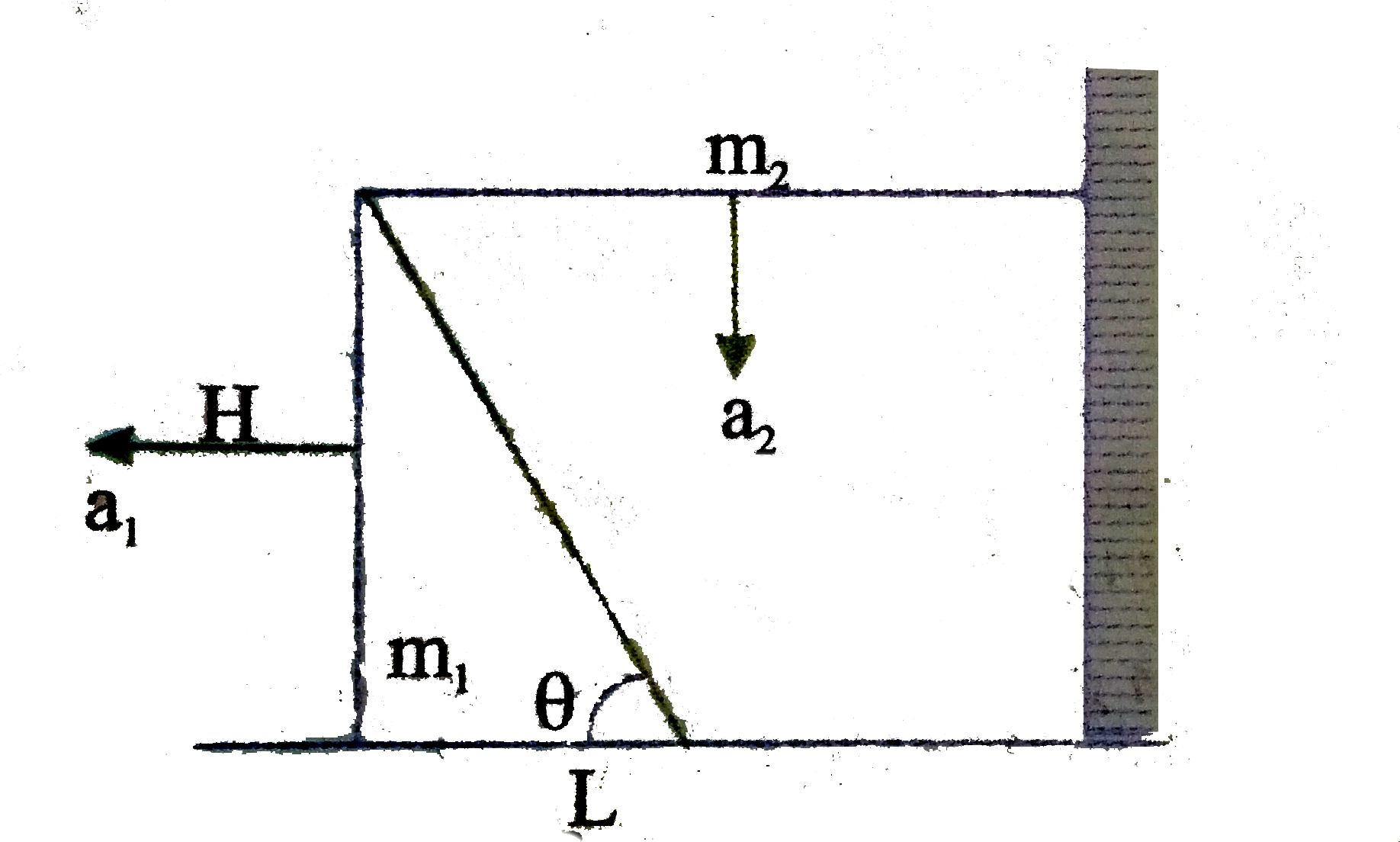 .
.
View SolutionA planet moving around sun sweeps area A1 in 2 days, A2 in 3 days and A3 in 6 days, then find the relation between A1,A2andA3

View SolutionUsing contraint equation. Find the relation between a1anda2.
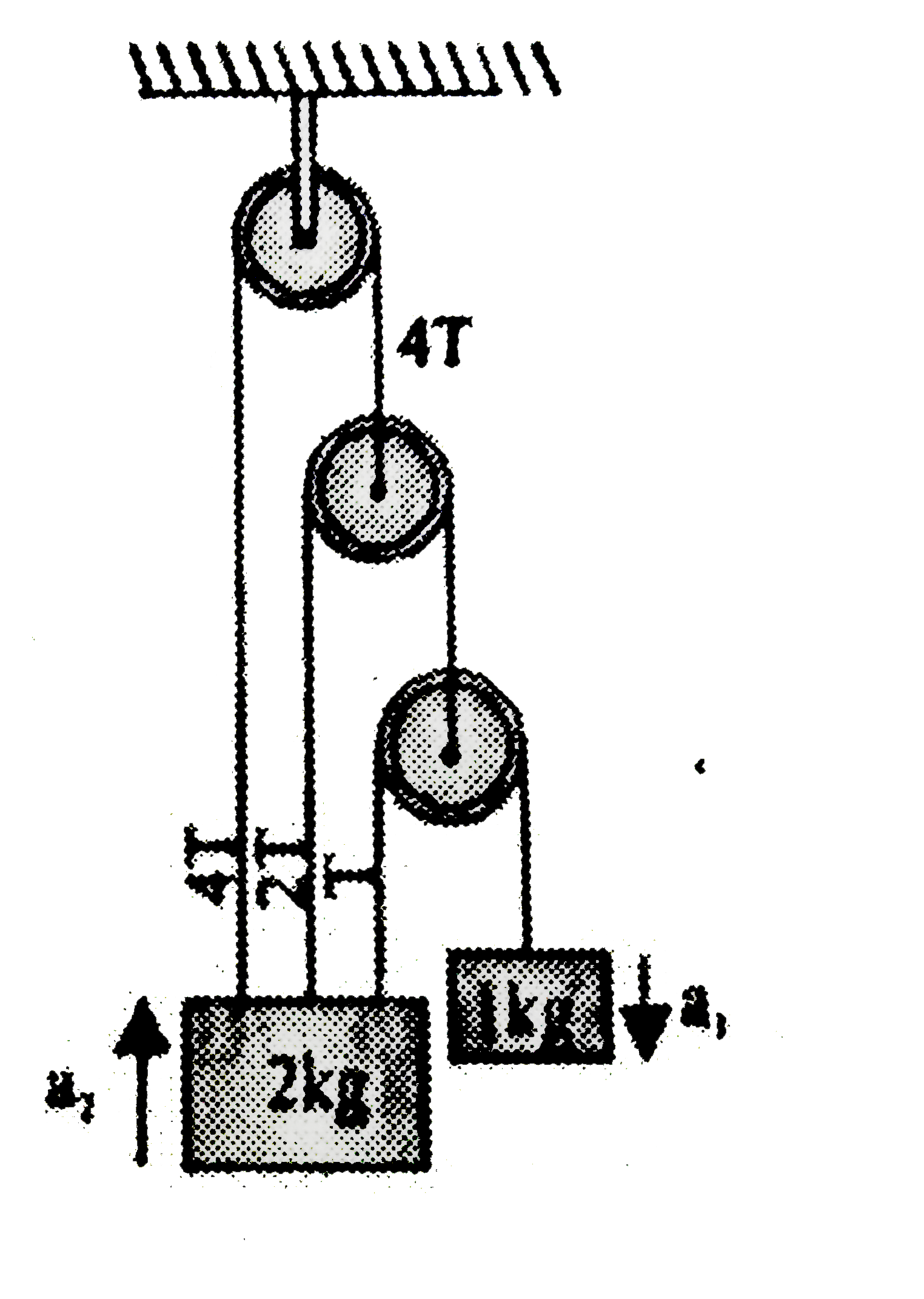
View SolutionUsing constraint method find the relation between of a1 and a2.

View SolutionFind the relation between acceleration a1 and a2
View Solution
