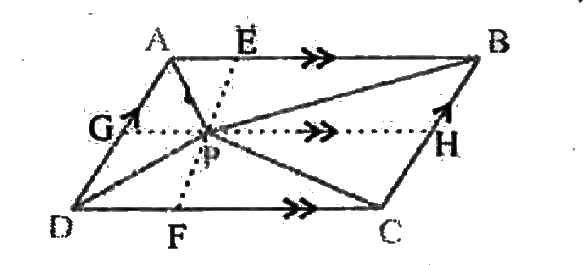
चित्र में दिया है कि ar(ΔDRC)=ar(ΔDPC) तथा ar(ΔARC)=ar(ΔARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD तथा DCPR समलंब चतुर्भुज हैं।
दिया है,
ar(ΔDRC)=ar(ΔDPC) ...(i)
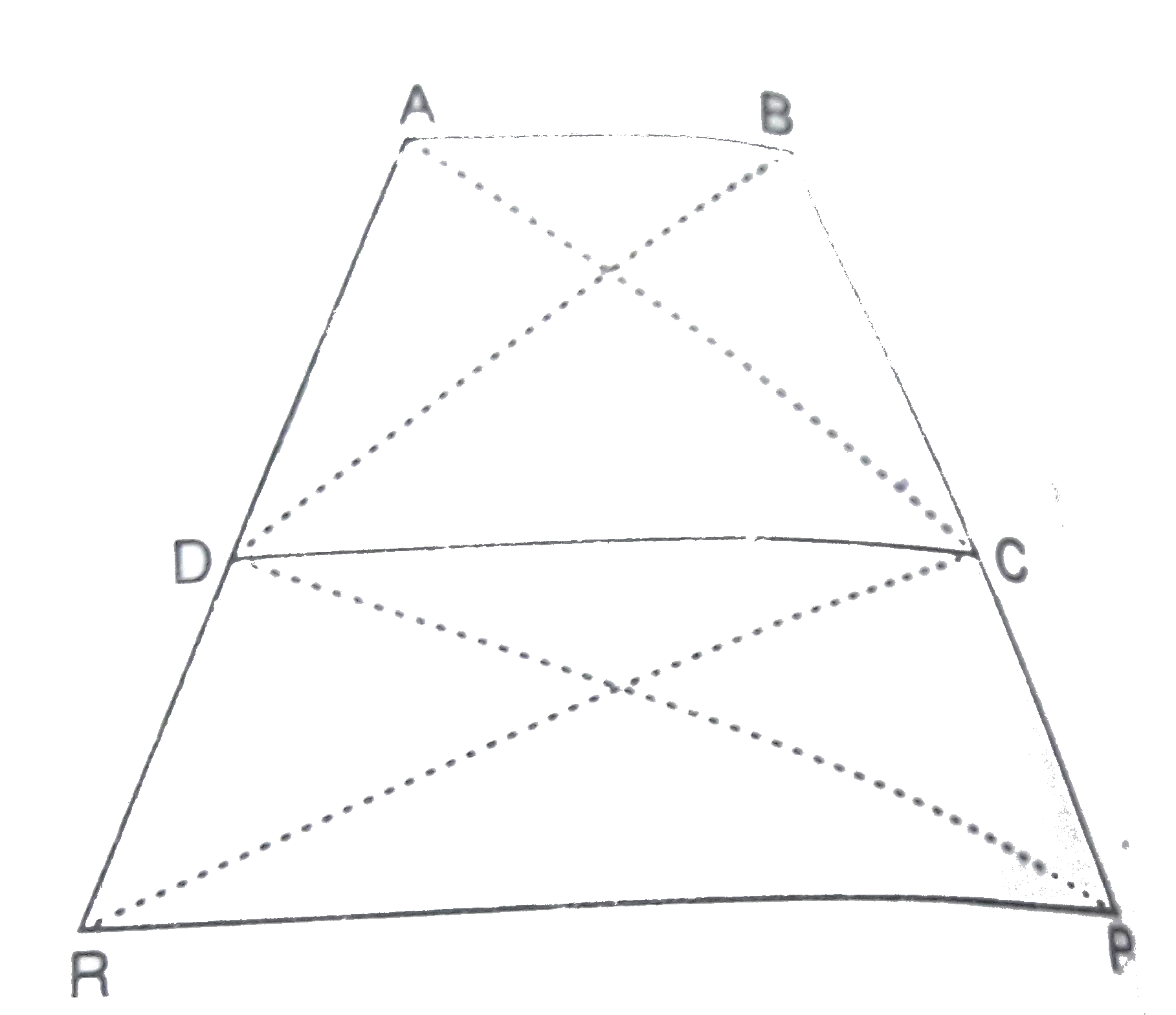
स्पष्ट है, त्रिभुज DRC तथा DPC एक ही आधार CD पर स्थित है, तथा इनके क्षेत्रफल भी समान है। अतः यह आवश्यक है कि वे एक ही समांतर रेखाओं के बीच स्थित हों।
अतः RP ।। DC ⇒ DCPR एक समलंब है।
यह भी दिया है कि,
ar(ΔARC)=ar(ΔBDP) ...(ii)
(ii) में से (i ) से सांगत पक्षों को घटाने पर,
ar(ΔARC)−ar(ΔDRC)=ar(ΔBDP)−ar(ΔDPC)
⇒ar(ΔADC)=ar(ΔBDC)
⇒ AD ।। DC
[ ∵Δ ADC तथा ΔBDC एक ही आधार DC पर स्थित है एवं उनके क्षेत्रफल भी बराबर है ]
⇒ABCD एक समलंब है।
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण
1 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.1
6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionIn the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
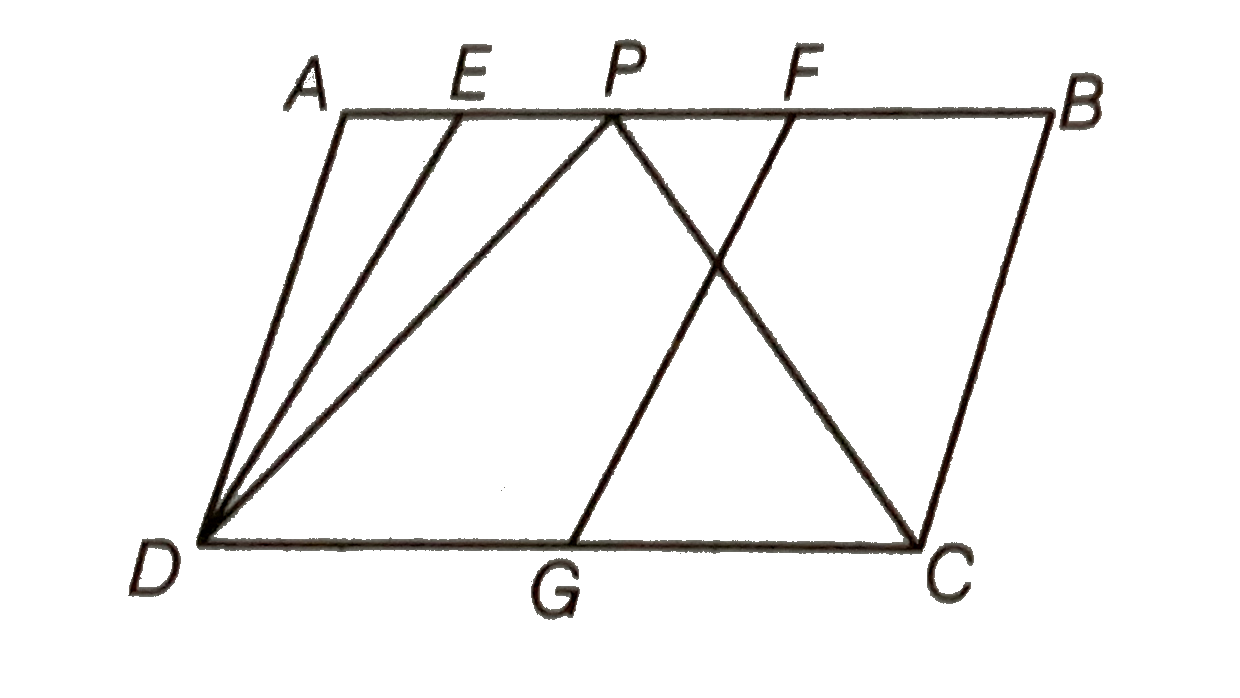
View Solutionआकृति में में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(APB)+ar(PCD)=12ar(ABCD)
(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View Solutionआकृति में ar(DRC)=ar(DPC) है और ar(BDP)=ar(ARC) है । दर्शाइए की दोनों चतुर्भुज ABCD और DCPR समलंब है ।
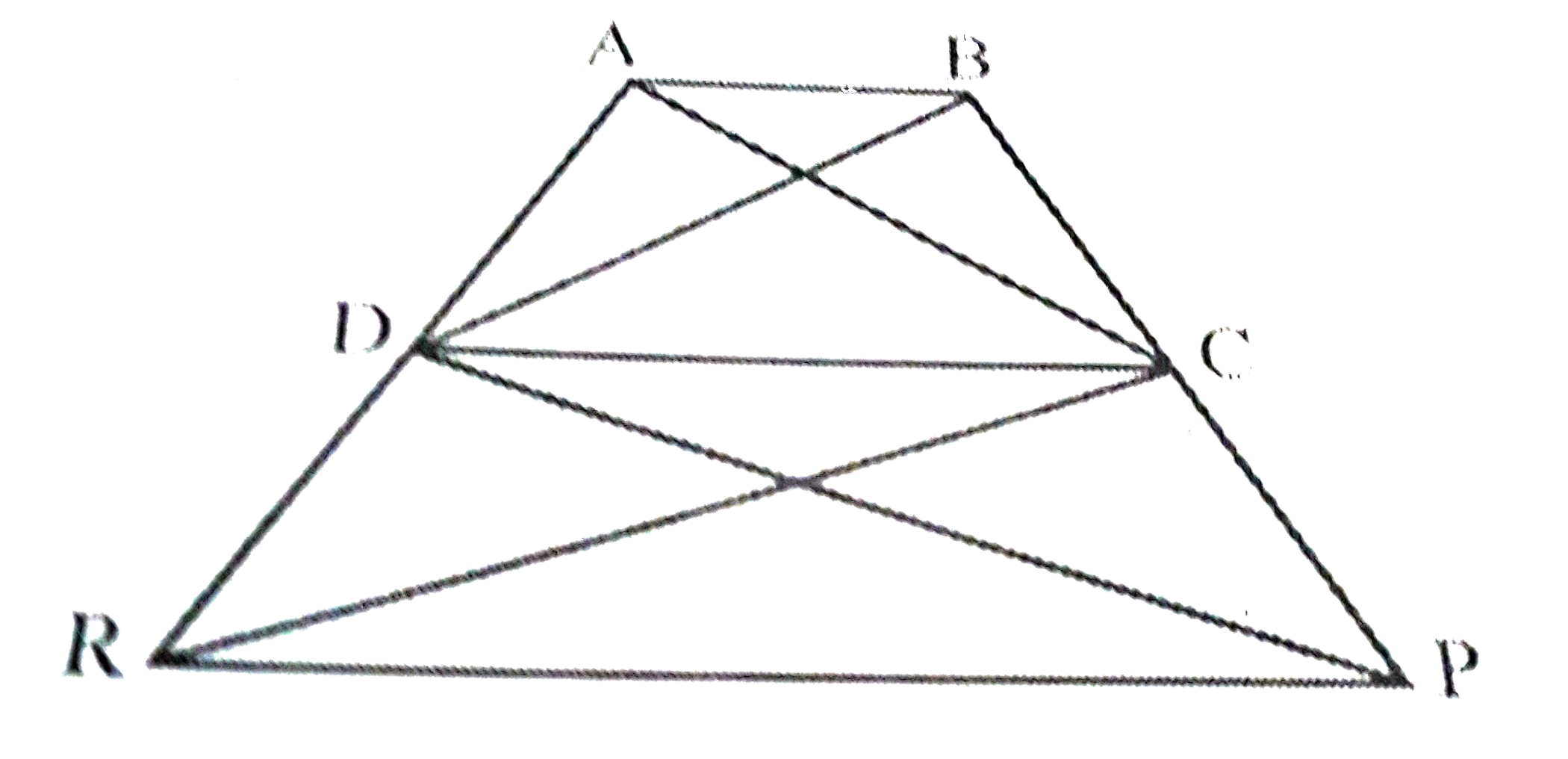
View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
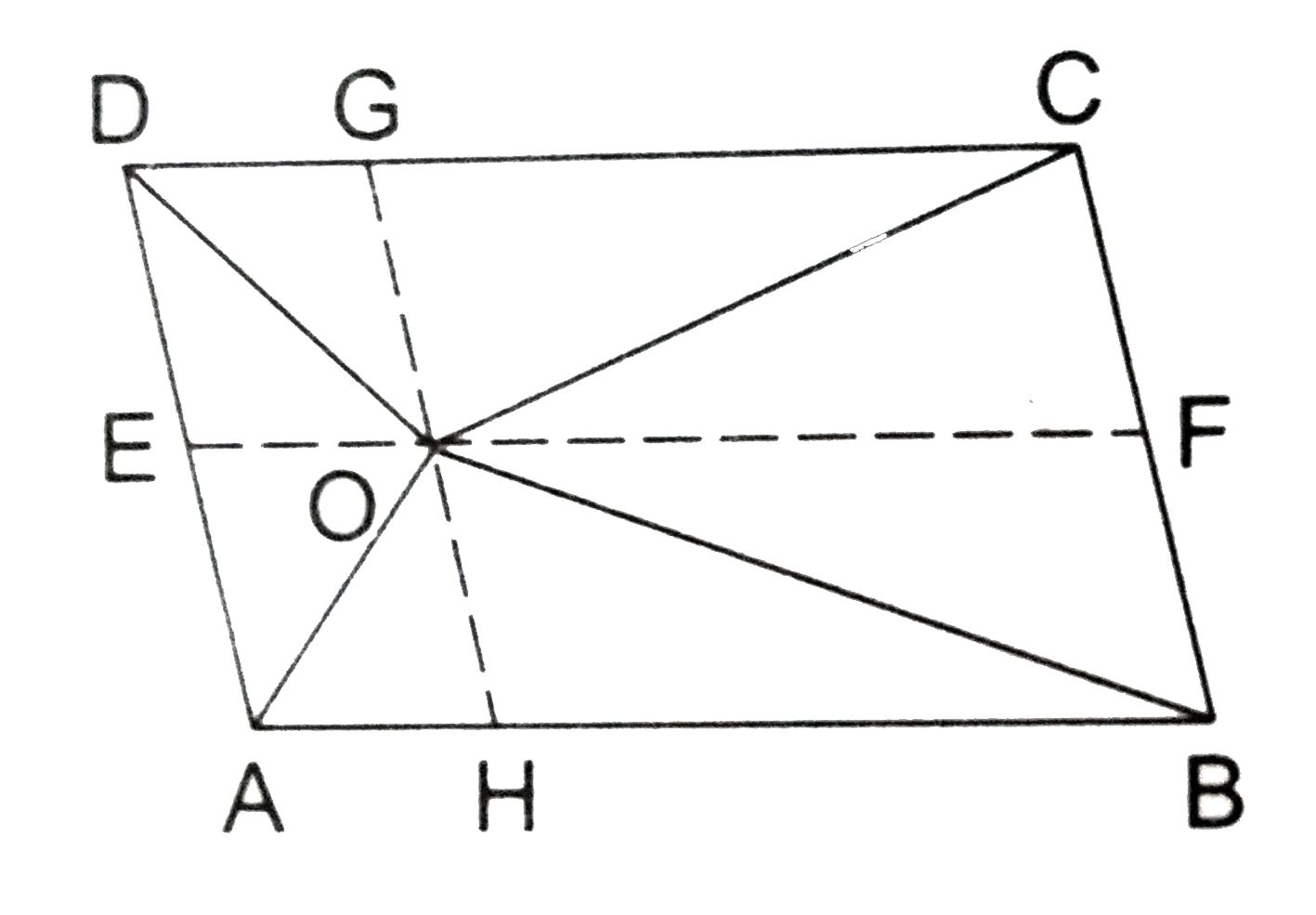
View Solutionदिखाइए कि अनुक्रम a,ar,ar2,......,arn−1 तथा A,AR,AR2,.......,ARn−1 के संगत पदों के गुणनफल से बना अनुक्रम गुणोत्तर श्रेढ़ी होती है तथा सार्व अनुपात ज्ञात कीजिए।
View SolutionABCD एक समांतर चतुर्भुज है तथा O इसके अन्तः क्षेत्र में स्थित कोई बिंदु है सिद्ध कीजिए कि
(i) ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
(ii) ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionΔABC में, भुजाओं AB तथा BC के मध्य-बिंदु क्रमशः P तथा Q है और AP का मध्य-बिंदु R है। सिद्ध कीजिए कि
(i)ar(ΔPBQ)=ar(ΔARC) (ii)ar(ΔPRQ)=12ar(ΔARC)
(iii)ar(ΔRQC)=38ar(ΔABC)
View Solutionदिए गए चित्र में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है |दर्शाइए की
(i)ar(APB)+ar(PCD)=12ar(ABCD)
ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View Solutionयदि ΔABC~ΔPQR तथा BC=5QR तो ar(ΔABC):ar(ΔPQR) है
View SolutionIn P is a point in the interior of a parallelogram ABCD. Show that<br>(ii)ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
View Solution
