किसी G.P. का प्रथम पद 729 एवं सातवाँ पद 64 है। इसके प्रथम सात पदों का योगफल ज्ञात करे।
प्रश्न से, a=729,t7=64
अब t7=64⇒ar5=64
⇒724.26=64
⇒r6=64729=(±23)6
⇒r=±23
जब r2=23,S1=a(1−r2)1−r=729[1−(23)]1−23
=729×3(1−1282187)
=2187(1−1282187) =2187−128=2059
जब r=−23,S7=729[1−(−23)7]1+23
=21875(1+1282187)
=15(2187+128)=15(2315)=463
अतः Sn=2059 या 463
Topper's Solved these Questions
- अनुक्रम तथा श्रेणी BOOK - KC SINHACHAPTER - अनुक्रम तथा श्रेणी EXERCISE - अभ्यास 15.1
27 Videos
- अनुक्रम तथा श्रेणी BOOK - KC SINHACHAPTER - अनुक्रम तथा श्रेणी EXERCISE - अभ्यास 15.2
25 Videos
- अनुक्रम तथा श्रेणी BOOK - KC SINHACHAPTER - अनुक्रम तथा श्रेणी EXERCISE - वस्तुनिष्ठ प्रश्न
4 Videos
- SINE तथा COSINE का सूत्र और उनके अनुप्रयोग BOOK - KC SINHACHAPTER - SINE तथा COSINE का सूत्र और उनके अनुप्रयोग EXERCISE - बहुकल्पीय प्रश्न
30 Videos
- अवकलज या अवकल गुणांक BOOK - KC SINHACHAPTER - अवकलज या अवकल गुणांक EXERCISE - वस्तुनिष्ठ प्रश्न
10 Videos
Similar Questions
दी गई परिभाषाओं के आधार पर निम्नलिखित प्रत्येक अनुक्रम के प्रथम तीन पद बताइए :
tn=3n+1
View Solutionअनुक्रम 10, 5, 0, -5, -10,…….. का 10वा पद ज्ञात कीजिए।
View Solutionश्रेढ़ी 1.4+3.7+5.10+.......... के n पदों का योगफल है
View Solution△ABC में tan(A2)=
View Solutionअगर y=(x−a)(x−b), , तब x का मान जिसके लिए dydx=0 is
View Solutionउन श्रेढियों के n पदों तक योगफल ज्ञात कीजिए जिनके n वे पद निम्नलिखित है -
n3−3n2+2n
View Solutionश्रेढी 2×4+4×6+6×8+….. का 20 वां पद और 20 पदों का योगफल ज्ञात कीजिए ।
View Solution(1+2x)5/2 का प्रथम ऋणात्मक पद ज्ञात कीजिए|
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionएक समान्तर श्रेढ़ी में पदों की संख्या सम ( even ) है| उसके विषम पदों का योग 24 तथा सम पदों का योग 30 है और अंतिम पद, प्रथम पद से 1012 अधिक है | पसं की संख्या एवं श्रेढ़ी ज्ञात कीजिए |
View Solutionकिसी समान्तर श्रेढी का 54 वाँ पद -61 तथा चौथा पद 64 है । उसका 32 वाँ पद ज्ञात कीजिए ।
View Solutionएक श्रेणी जिसका n वा पद nx+y है के r पदों का योगफल होगा
View Solutionसमांतर श्रेणी | समांतर श्रेणी का व्यापक पद | समांतर श्रेणी के N पदों का योगफल | उदाहरण
View Solutionगुणोत्तर श्रेणी | गुणोत्तर श्रेणी का व्यापक पद | गुणोत्तर श्रेणी के N पदों का योगफल | उदाहरण
View Solutionनिम्नलिखित सारणी में, रिक्त स्थानों को भरिए, जहाँ A.P. का प्रथम पद a , सार्व अंतर d और nवाँ पद a_nहै:
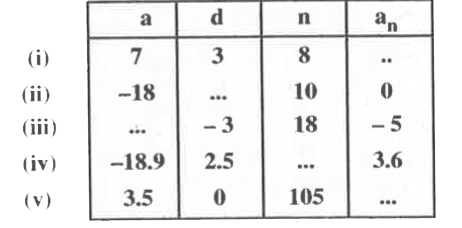
View Solution(1) किसी A.P. के प्रथम 10 पदों का योगफल ज्ञात कीजिए यदि T1=−14 और T5=20.
(ii) किसी A.P. का तीसरा पद 14 और 8वाँ पद 34 है।Sn और S30 ज्ञात कीजिए।
View Solution
