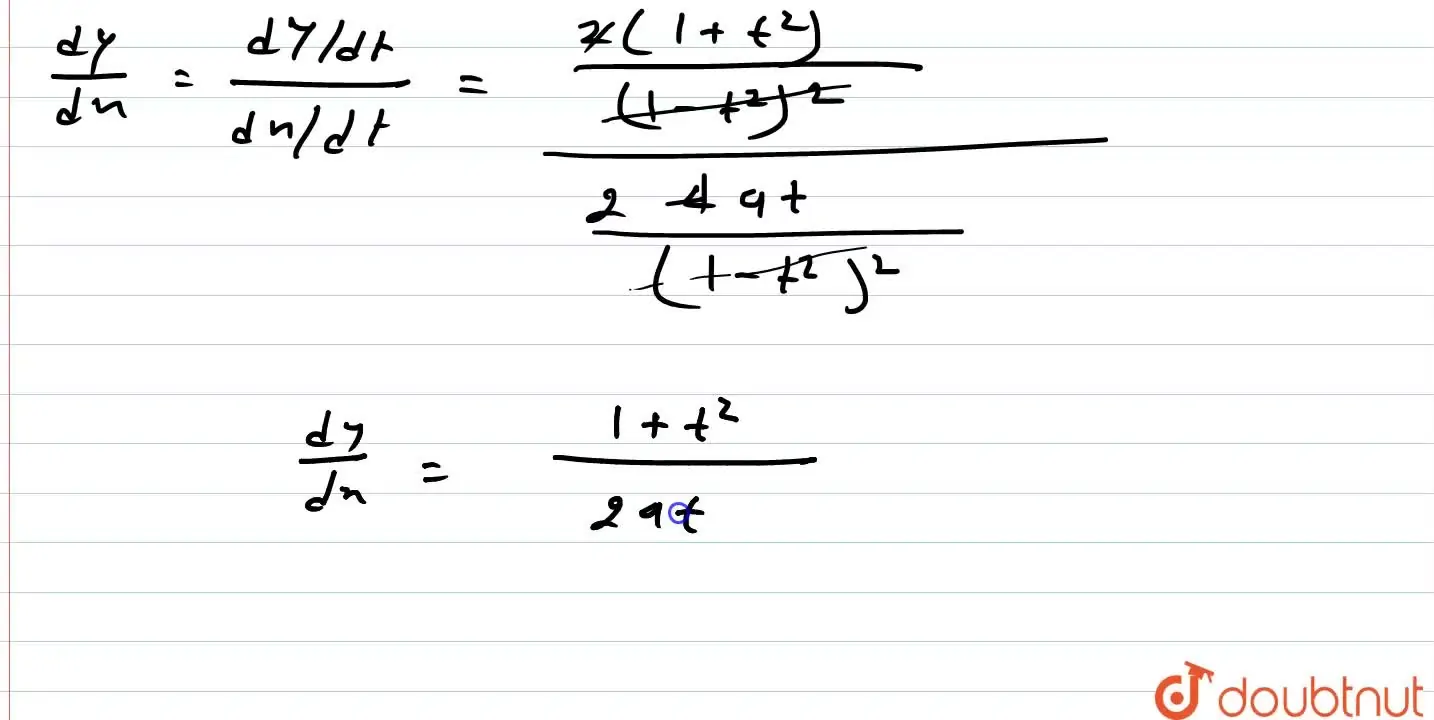यदि x=a(1+t2a−t2) व y=2t(1−t2) तब dydx का मान ज्ञात कीजिए|
यहाँ x=a(1+t21−t2)=a[−1+21−t2]
=a[−1+2(1−t2)−1(−2t)]
t के सापेक्ष अवकलन करने पर
dxdy=a[0+2(−1)(1−t2)−2(−2t)]
=a×4t(1−t2)2=4at(1−t2)2
अब y=2t(1−t2)
t के सापेक्ष करने पर
dydt=(1−t2)⋅2−2t(−2t)(1−t2)2=2(1+t2)(1−t2)2
इसलिए dydx=(dydt×dtdx)
=⎧⎨⎩2(1+t2)(1−t2)2×(1−t2)24at⎫⎬⎭=(1+t2)2at
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - निहित फलनों का अवकलन EXERCISE - अभ्यास प्रश्न 8.121videos
निहित फलनों का अवकलन
- BOOK - BALAJI PUBLICATIONCHAPTER - निहित फलनों का अवकलन EXERCISE - अभ्यास प्रश्न 8.235videos
निहित फलनों का अवकलन
- BOOK - BALAJI PUBLICATIONCHAPTER - निश्चित समाकलन EXERCISE - स्वमूल्यांकन परीक्षण31videos
निश्चित समाकलन
- BOOK - BALAJI PUBLICATIONCHAPTER - प्रतिलोम त्रिकोणमितीय फलनEXERCISE - स्वमूल्यांकन परीक्षण34videos
प्रतिलोम त्रिकोणमितीय फलन
Similar Questions
फलन का अवकल गुणांक ज्ञात कीजिए| sin3x
05:33View Solutionफलन का x के सापेक्ष अवकल गुणांक ज्ञात कीजिए| e√sinx+√cosx
02:30View Solution∫π/20cos2xdx
04:39View Solutionसिद्ध कीजिए कि tan−11+tan−112+tan−113=π4
07:56View SolutionIf x=a(1+t21−t2)andy=2t1−t2,f i n ddydx
04:13View SolutionIf x=1−t21+t2 and y=2t1+t2 ,then dydx=
03:57View SolutionIf x=1−t21+t2 and y=2t1+t2, then dydx is equal to
02:15View Solutionयदि (If) x=a(1+t21−t2) तथा (and) y=2t1−t2, (find) dydx निकालें।
07:37View SolutionIf x=2t1+t2,y=1−t21+t2, then dydx=
03:42View SolutionIf x=1−t21+t2 and y=2t1+t2, then: dydx∣∣∣t=1 is
07:33View Solutionx=1−t21+t2,y=2t1+t2 then dydx is
05:17View SolutionIf x=1−t21+t2andy=2t1+t2 then dydx at t=2………….
05:17View SolutionIf x=2t1+t2,y=1−t21+t2,thenfinddydx.
02:52View SolutionIF [x=a{1+t21−t2] and [y=2t1−t2] find dy/dx.
07:55View SolutionIf x=1−t21+t2 and y=2t1+t2, then dydx is equal to
02:59View SolutionIf x=1−t21+t2 and y=2t1+t2 ,then dydx=
03:01View Solution