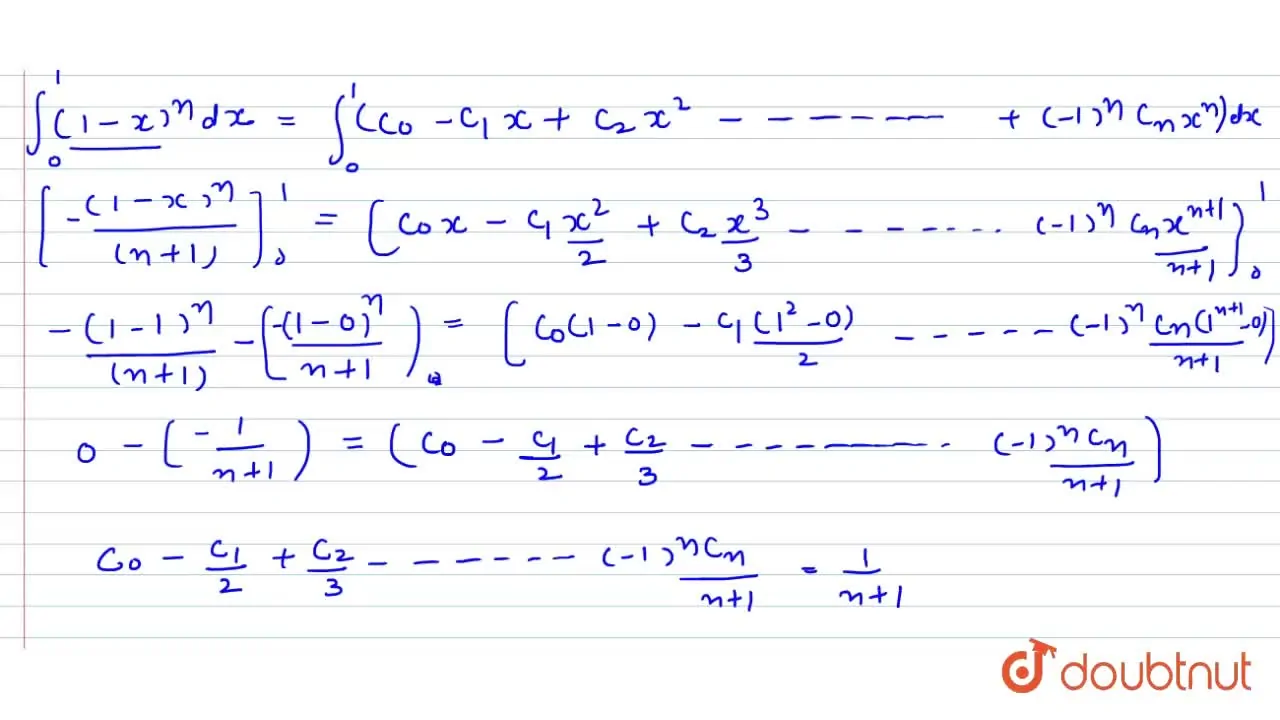यदि (1+x)n=C0+C1x+C2x2+...+Cnxn तो साबित कीजिए कि
C0−C12+C23−......+(−1)nCnn+1=1n+1
दिया गया श्रेणी है : C0−C12+C23−...+(−1)n.Cnn+1
r वाँ पद, tr=(−1)r−1nCr−1r
अब, C0−C12+C23−...+(−1)n.Cnn+1
=n+1∑r=1(−1)r−1.nCr−1r=n+1∑r=1(−1)r−1.n+1Crn+1 [∵nCr−1r=n+1Crn+1]
=1n+1[n+1C1−n+1C2+n+1C3−...+(−1)n.n+1Cn+1]
=1n+1[−n+1C0+n+1C1−n+1C2.+n+1C3−...+(−1)n.n+1Cn+1+n+1C0]
=1n+1[−{n+1C0−n+1C1+...+(−1)n+1.n+1Cn+1}+n+1C0]
=1n+1[−(1−1)n+1+n+1C0]=1n+1
Related Playlists
- BOOK - KC SINHACHAPTER - धन पूर्ण घातांक के लिए द्विपद प्रमेय EXERCISE - अभ्यास 14.126videos
धन पूर्ण घातांक के लिए द्विपद प्रमेय
- BOOK - KC SINHACHAPTER - धन पूर्ण घातांक के लिए द्विपद प्रमेय EXERCISE - अभ्यास 14.222videos
धन पूर्ण घातांक के लिए द्विपद प्रमेय
- BOOK - KC SINHACHAPTER - द्विघात समीकरण EXERCISE - प्रश्नावाली 11.131videos
द्विघात समीकरण
- BOOK - KC SINHACHAPTER - प्रायिकता या सम्भाविताEXERCISE - वस्तुनिष्ठ प्रश्न15videos
प्रायिकता या सम्भाविता
Similar Questions
द्विपद सिद्धान्त से निम्नांकित का विस्तार कीजिए
(x+1x)704:48View Solution(4x5−52x)9 के प्रसार में 7 वाँ पद ज्ञात कीजिए |
04:34View Solutionसमीकरण का हल गुणनखंडन विधि से ज्ञात कीजिए :
2x2+3=005:36View Solutionएक बैग में 5 सफ़ेद तथा 7 लाल गेंद है। एक लाल गेंद निकालने की प्रायिकता है :
03:37View Solutionयदि (1+x)n=C0+C1x+C2x2+.....+Cnxn. साबित कीजिए कि
C0.C1+C1.C2+..…+Cn−1.Cn=(2n)!(n+1)!(n−1)!05:24View SolutionIf (1+x)n=nC0+nC1x+nC2x2+…+nCnxn, prove that,
nC1−2nC2+3nC3−…+(−1)n−1.nnCn=0.04:35View SolutionIf (1+x)n=C0+C1x+C2x2
+…+Cnxn, prove that +32⋅C3+…+n2⋅Cn
12⋅C1+22⋅C2=n(n+1)⋅2n−2 .05:32View SolutionIf (1+x)n=C0+C1x+C2x2+C3x3+…+Cnxn , prove that
C0−C12+C23−…+(−1)nCnn+1=1n+1.05:07View SolutionIf (1+x)n=C0+C1x+C2x2+…+Cnxn , prove that
C20−C21+C22−…+(−1)n⋅C2n=0 or
(−1)n/2⋅n!(n/2)!(n/2)!, according as n is odd or even
Also , evaluate C20+C21+C22−...+(−1)n⋅C2n for n
= 10 and n= 11 .04:30View SolutionIf (1+x)n=C0+C1x+C2x2+.....+Cnxn then show :
C01+C12+C23+......+Cnn+1=2n+1−1n+105:36View SolutionIf (1+x)n=C0+C1x+C2x2+.....+Cnxn then show :
C01−C12+C23−......+(−1)n.Cnn+1=1n+104:44View SolutionIf (1+x)n=C0+C1x+C2x2+.....+Cnxn then show :
C0.Cn+C1.Cn−1+C2.Cn−2+....+Cn.C0=(2n)!(n!)203:21View SolutionIf (1+x)n=C0+C1x+C2x2+.....+Cnxn then show :
C1C0+2C2C1+3C3C2+....+nCnCn−1=n(n−1)204:10View SolutionIf (1+x)n=C0+C1x+C2x2+.....+Cnxn then show :
C0C1+C1C2+C2C3+.....+C_(n−1)Cn=(2n)!(n+1)!(n−1)!View SolutionIf (1+x)n=C0+C1+x+C2x2+...+Cnxn show that,
C0−22⋅C1+32⋅C2−...+(−1)n⋅(n+1)2⋅Cn=0(n>2)03:32View Solution