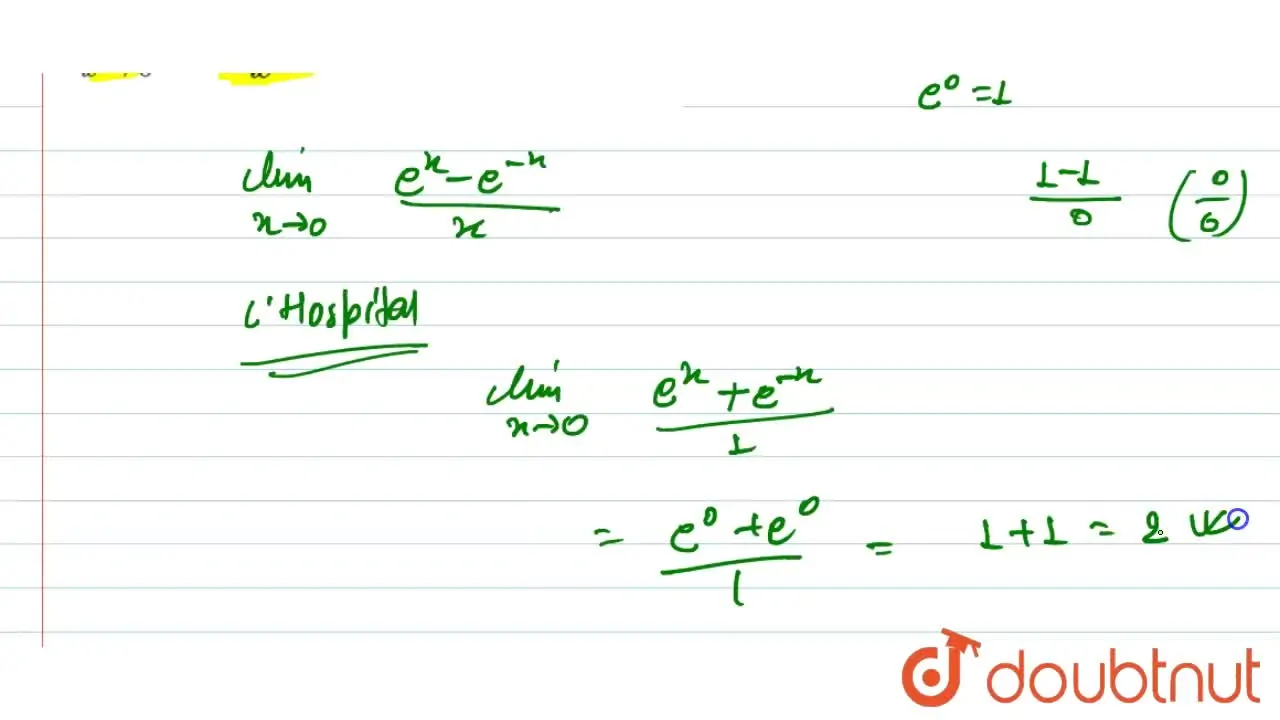
limx→0ex−e−xx का मान ज्ञात कीजिए ।
2
5
7
3
The correct Answer is:A
limh→0ex−exx=limx→01x[(1+x+x22!+x33!+....)−[(1−x+x22!−x33!+....)]
=limx→01x[2(x−x33![2(x−x33!+......)]
=limx→0[2(1+x23!+......)] [∵x≠0]
=2.
Related Playlists
Similar Questions
निम्नलिखित प्रश्नो के मान ज्ञात कीजिये :
limx→02sin24xx201:59View Solutionनिम्नलिखित फलनों का x के साक्षेप अवकल - गुणांक ज्ञात कीजिए ।
sinxcosx,cosecx01:52View Solutionएक कक्षा के सभी विधार्थियों ने गणित में कम अंक प्राप्त किये । अध्यापक ने प्रत्येक विधार्थी को 10 रियायती अंक देने का निर्णय लिया । रियायती अंक देने के बाद भी निम्नलिखित में से कौन - सी सांख्यिकी माप नहीं बदलेगी ?
View Solution∫xsin3x2cosx2dx का मान ज्ञात कीजिए।
03:40View Solution∫tanx dx का मान ज्ञात कीजिए।
02:50View Solutionlim_(x to 0)(sin(a+b)x+sin(a-b)x+sin2ax)/((2 sin(a+b)x*sin(a-b)) का मान ज्ञात कीजिए।
02:56View Solutionlimx→asinx−sina√x−√a का मान ज्ञात कीजिए ।
02:46View Solutionlimx→πsin(π−x)π(π−x) का मान ज्ञात कीजिए ।
03:11View Solutionlimx→∞2xsin(a2x) का मान ज्ञात कीजिए ।
03:18View Solutionनिम्नलिखित निश्चित समकलो का मान ज्ञात कीजिए :
∫π0xsinxdx04:10View Solutionनिम्न का x की आरोही घातों में प्रसार ज्ञात कीजिए :
e4x+e2xe3x04:10View Solutionनिम्न का x की आरोही घातों में प्रसार ज्ञात कीजिए :
e3x+e−xex01:28View Solutionनिम्न का x की आरोही घातों में प्रसार ज्ञात कीजिए :
e3x−e−xex05:52View Solutionlimx→034x−33x−3x+1x2 का मान ज्ञात कीजिए ।
07:57View Solutionlimx→∞sinxx का मान ज्ञात कीजिए ।
03:28View Solution