एक पतंग जमीन के तल से की ऊंचाई पर उड़ रही है। यह क्षैतिज से पर झुकी हुई एक डोरी से बंधी है। डोरी की लम्बाई है:
m
m
The correct Answer is:B
Step by step video, text & image solution for एक पतंग जमीन के तल से 75m की ऊंचाई पर उड़ रही है। यह क्षैतिज से 60^(@) पर झुकी हुई एक डोरी से बंधी है। डोरी की लम्बाई है: by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - UP BOARD PREVIOUS YEARCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - अतिलघु उत्तरीय प्रश्न2videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - UP BOARD PREVIOUS YEARCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - लघु उत्तरीय प्रश्न2videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - UP BOARD PREVIOUS YEARCHAPTER - त्रिकोणमिति का परिचय EXERCISE - लघु उत्तरीय प्रश्नोत्तर6videos
त्रिकोणमिति का परिचय
- BOOK - UP BOARD PREVIOUS YEARCHAPTER - त्रिभुज EXERCISE - दीर्घ उत्तरीय प्रश्न11videos
त्रिभुज
Similar Questions
एक मीनार की ऊंचाई 20 मीटर है। जमीन पर बनने वाली इसकी छाया की लम्बाई 20√3 मीटर है। सूर्य का उन्नयन कोण ज्ञात कीजिए।
04:43View Solutionएक आदमी और एक बच्चा जमीन पर 2 मीटर दूरी पर खड़े हुए हैं। आदमी की ऊंचाई बच्चे की ऊंचाई की 4 गुनी है यदि उनके पादों को मिलाने वाले रेखाखंड के मध्य-बिंदु पर उनके शीर्षों के उन्नयन कोण पूरक हों तों बच्चे की ऊंचाई ज्ञात कीजिए।
05:01View Solutionयदि A ,B ,C किस त्रिभुज के अन्तः कोण हो, तो सिद्ध कीजिए :
04:14View Solutionआकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि ar(ΔABC)ar(ΔDBC)=AODO है।
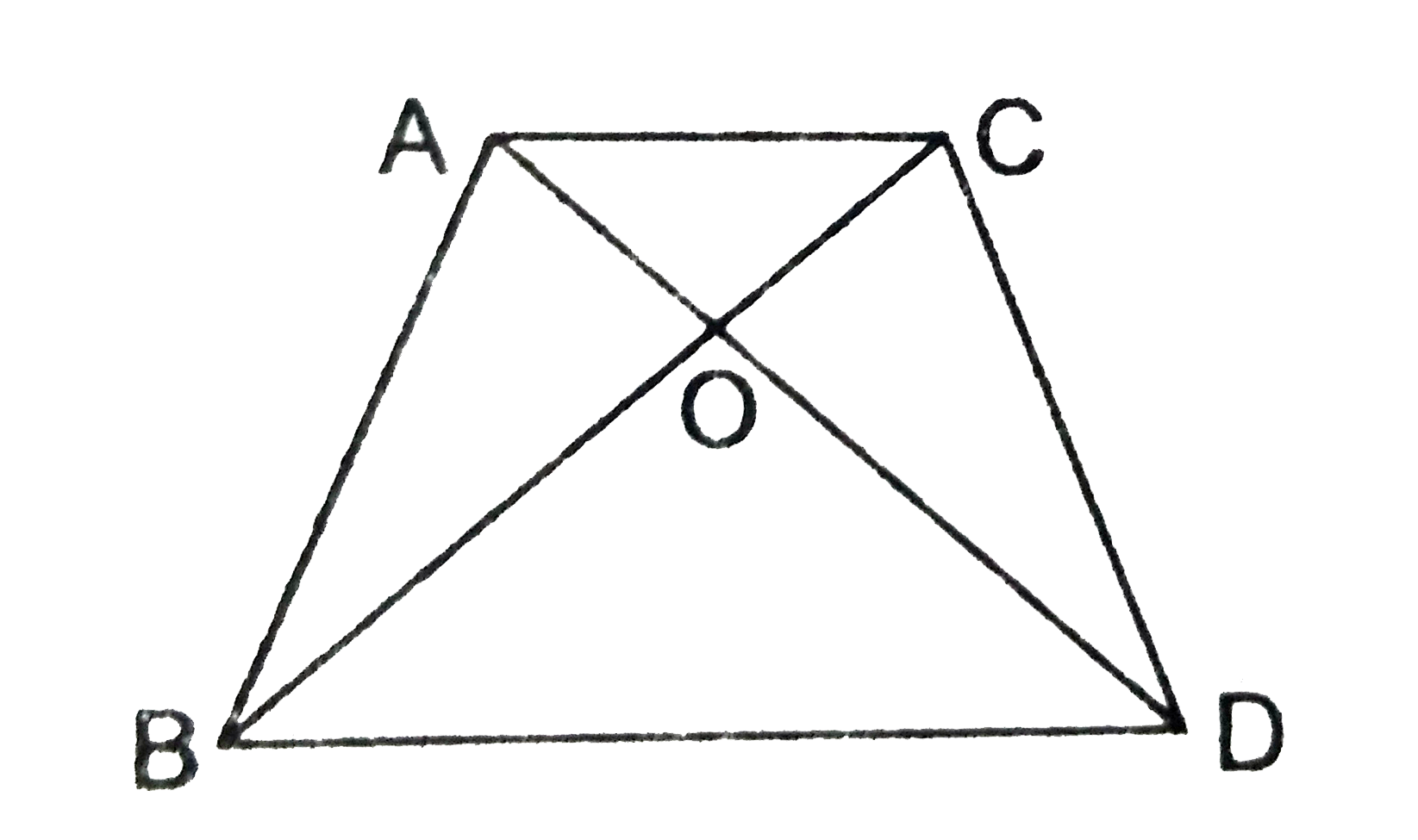 02:29View Solution
02:29View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
04:26View Solutionएक 13 मीटर लम्बी सीढ़ी दीवार के सहारे झुकी हुई है। सीढ़ी के पाद को 1.5 मी./से. की दर से जमीन के सारे दीवार से दूर खींचा जाता है। सीढ़ी तथा जमीन के मध्य का कोण किस गति से परिवर्तित हो रहा है जबकि सीढ़ का पावि दीवार से 12 मीटर दूर हो ।
04:06View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
02:42View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
02:26View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
01:57View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
03:25View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
01:36View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
01:39View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
01:47View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
03:49View SolutionThe string of a kite is 30m long and it makes an angle 60^@ with the horizontal. The height of the kite above the ground is: पतंग की डोर 30 मी लंबी है और यह क्षेतिज से 60^@ का कोण बनाती है। जमीन के ऊपर पतंग की ऊंचाई है:
View SolutionSeema flies a kite on a 16 m string at an inclination of 60^@ . What is the height (h) of the kite above the ground? सीमा 60^@ के झुकाव पर 16 मीटर के धागे से एक पतंग उड़ाती है | भूमि से पतंग की ऊंचाई कितनी है ?
View Solution
