एक झील की सतह से 60 मीटर ऊँचे बादलों का उन्नयन कोण 30∘ है|तथा बादलों की परछाई का उसी बिंदु पर अवनमन कोण 60∘ है|बादलों की ऊंचाई ज्ञात कीजिए|
माना AB झील की सतह है P निरिक्षण बिंदु है|
C बादलों की स्थिति तथा C झील में बादलों की परछाई इस प्रकार है की|
CB=C'B
P से CC' पर लम्ब PQ खींचे|
तब ∠CPQ=30∘
तथा ∠C'PQ=60∘
यदि CQ=h तब C'B=h+60
अब ΔCQP में tan30∘=CQPQ ⇒ 1√3=hPQ
⇒ PQ=h√3 ...(1)
पुनः ΔPQC में, tan60∘=C'QPQ
⇒ √3=C'B+BQPQ=h+60+60PQ
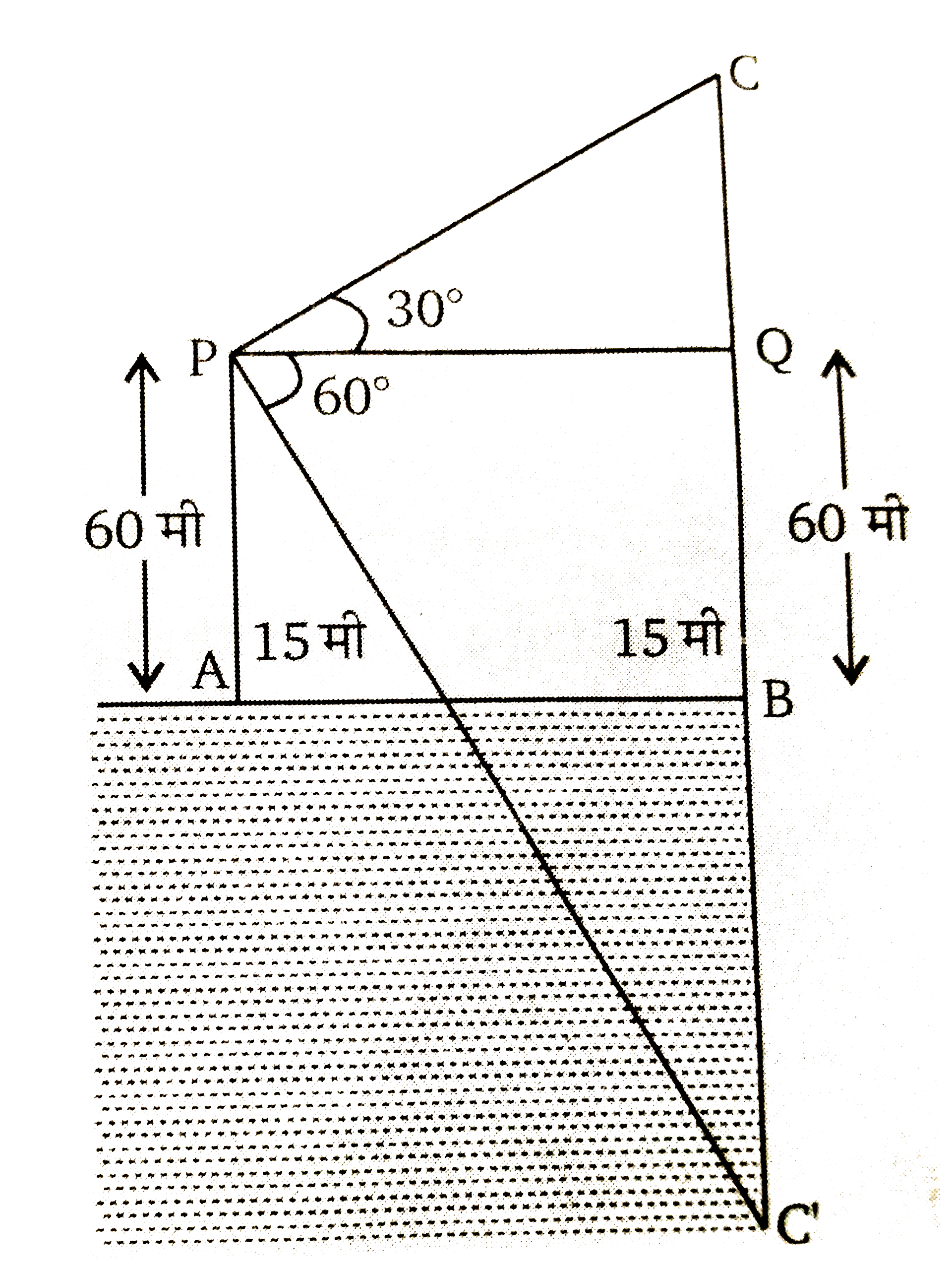
⇒ PQ=h+120√3 ...(2)
समीकरण (1 ) व (2 ) से, h√3=h+120√3
h के लिए हल करने पर h=60
∴ अभीष्ट ऊंचाई CB=h+60+60=120
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - ऊँचाई एवं दुरी EXERCISE - अभ्यास प्रश्न 11.119videos
ऊँचाई एवं दुरी
- BOOK - BALAJI PUBLICATIONCHAPTER - ऊँचाई एवं दुरी EXERCISE - अभ्यास प्रश्न 11.226videos
ऊँचाई एवं दुरी
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण35videos
त्रिकोणमितीय अनुपात एव असमिकाएँ
Similar Questions
जिस समय सूर्य का उन्नयन कोण 45∘ था तो एक मीनार की परछाई,उस मीनार की लम्बाई से-
05:01View Solutionएक ऊर्ध्वाधर खम्भे की छाया उसकी ऊंचाई के बराबर है तो सूर्य का उन्नयन कोण होगा?
03:52View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
02:20View Solutionबिंदु A(1,2) से होकर जाने वाली रेखा X-अक्ष के साथ 60∘ का कोण बनाती है तथा x+y=6 को बिंदु P पर काटती है तो AP की लम्बाई ज्ञात कीजिए
05:33View Solutionएक सदिश ¯¯¯¯¯¯OA,OX से 60∘ का कोण बनाता है और OY से 45∘ का कोण बनाता है तथा ∣∣¯¯¯¯¯¯OA∣∣=10 इकाई है। बिंदु A का स्थिति सदिश ज्ञात कीजिए।
02:59View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
04:42View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
02:01View Solutionएक रेखा x- अक्ष से 120∘ तथा y-अक्ष से 60∘ का कोण बनाती है, तो रेखा द्वारा z-अक्ष से बना कोण ज्ञात कीजिए।
02:30View Solutionएक झील से 25 मी ऊपर एक बिन्दु P से एक बदल का उन्नयन कोण 30∘ है तथा P से झील में बादल के प्रतिबिम्ब का अवनमन कोण 60∘ है, तो झील की सतह से बादल की ऊंचाई (मीटर में) है
04:25View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 36∘ का कोण बनाती है| बहुभुज की भुजाओं की संख्या ज्ञात कीजिए |
03:36View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
03:32View Solutionबादलों का बनना एक तीव्र परिवर्तन है।
04:59View SolutionA pole is standing on the top of a house. Height of house is 25 metres. The angle of elevation of the top of house from point P is 45^@ and the angle of elevation of the top of pole from P is 60^@ . Point P is on the ground level. What is the height (in meteres) of pole? एक घर की चोटी पर एक खम्भा खड़ा है। घर की ऊँचाई 25 मीटर है। बिंदु P से घर की चोटी का उन्नयन कोण 45^@ है तथा P से खम्भे की चोटी का उन्नयन कोण 60^@ है। बिंदु P भूमि कौ सतह पर है। खम्भे की ऊँचाई (मीटर में) क्या है?
View SolutionHeight of a tower is 120 metres. The angle of elevation of the top of tower from a point B is 75^@ .Point B is on the ground level. What is the distance (in metres)of point B from the base of tower? एक भीनार की ऊँचाई 120 मीटर है। बिंदु B से मीनार की चोटी का उन्नयन कोण 75^@ है। बिंदु B जमीन की सतह पर है। मीनार के आधार से बिंदु B की दूरी (मीटर में) क्या है?
04:08View SolutionA flag of height 4 metres is standing on the top of a building. The angle of elevation of the top of the flag from a point X is 45^@ and the angle of elevation of the top of building from X is 30^@ .Point X is on the ground level. What is the height (in metres) of the building? एक झंडा जिसकी ऊँचाई 4 मीटर है, इस इमारत की चोटी पर खड़ा हुआ है। बिंदु X से झंडे की चोटी का उन्नयन कोण 45^@ है तथा X से इमारत की चोटी का उन्नयन कोण 30^@ है। बिंदु X जमीन की सतह पर है। इमारत की ऊँचाई (मीटर में) क्या है?
04:30View Solution


