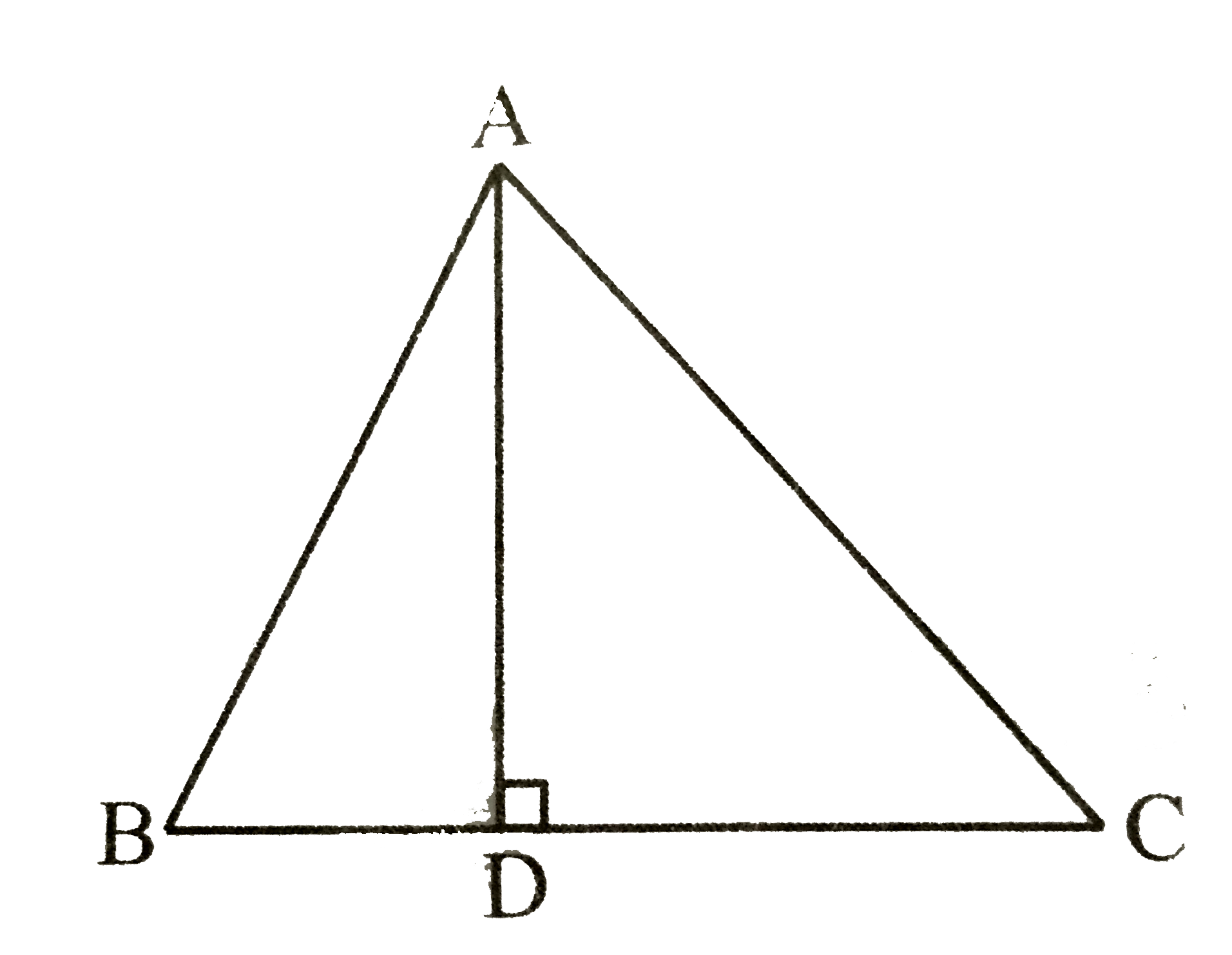
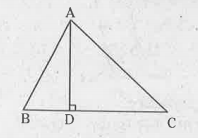
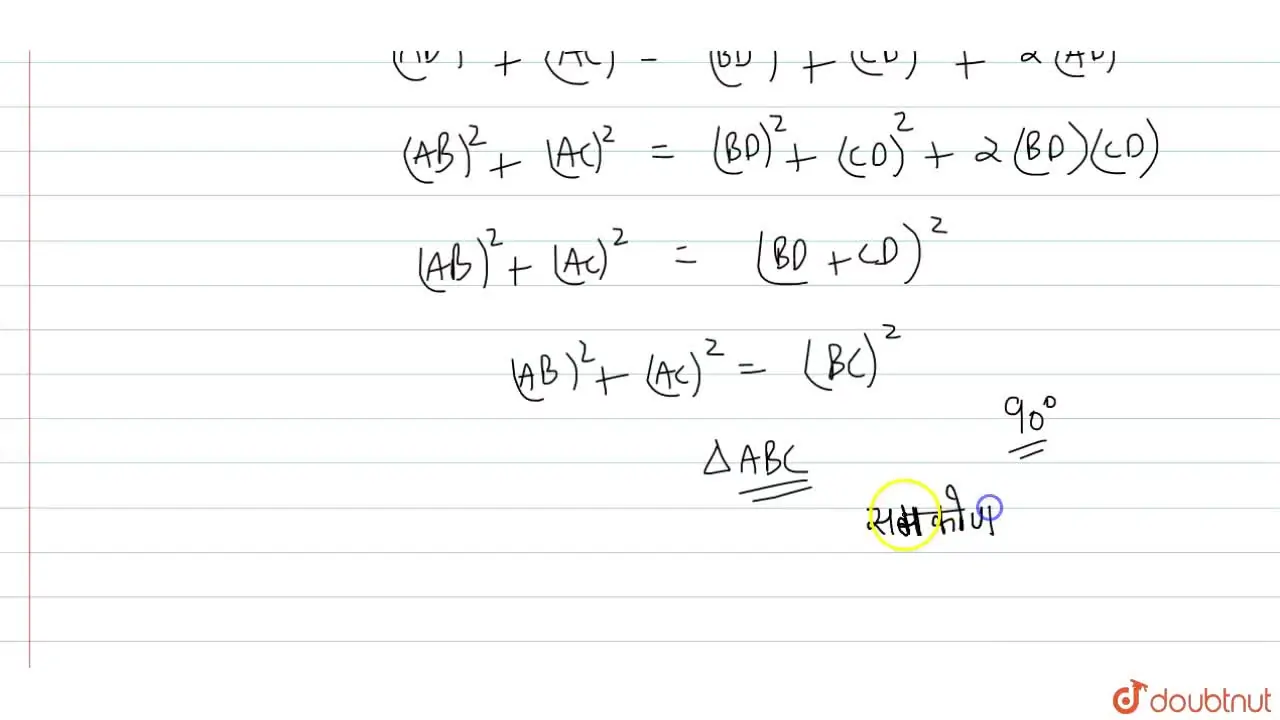एक △ABC में, AD⊥BC तथा AD2=BD×CD है तो सिद्ध कीजिए कि △ABC का समकोण त्रिभुज है |
अब समकोण △ADB तथा △ADC में यहाँ,
AB2=AD2+BD2 ...(1)
तथा AC2=AD2+DC2 ...(2)
समी० (1) तथा (2) को जोड़ने पर,
AB2+AC2=2AD2+BD2+DC2
=2BD×CD+BD2+CD2
=(BD+CD)2=BC2
⇒AB2+AC2=BC2
अतः △ABC एक समकोण त्रिभुज है |
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.19videos
त्रिभुज
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.217videos
त्रिभुज
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण35videos
त्रिकोणमितीय अनुपात एव असमिकाएँ
- BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण29videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
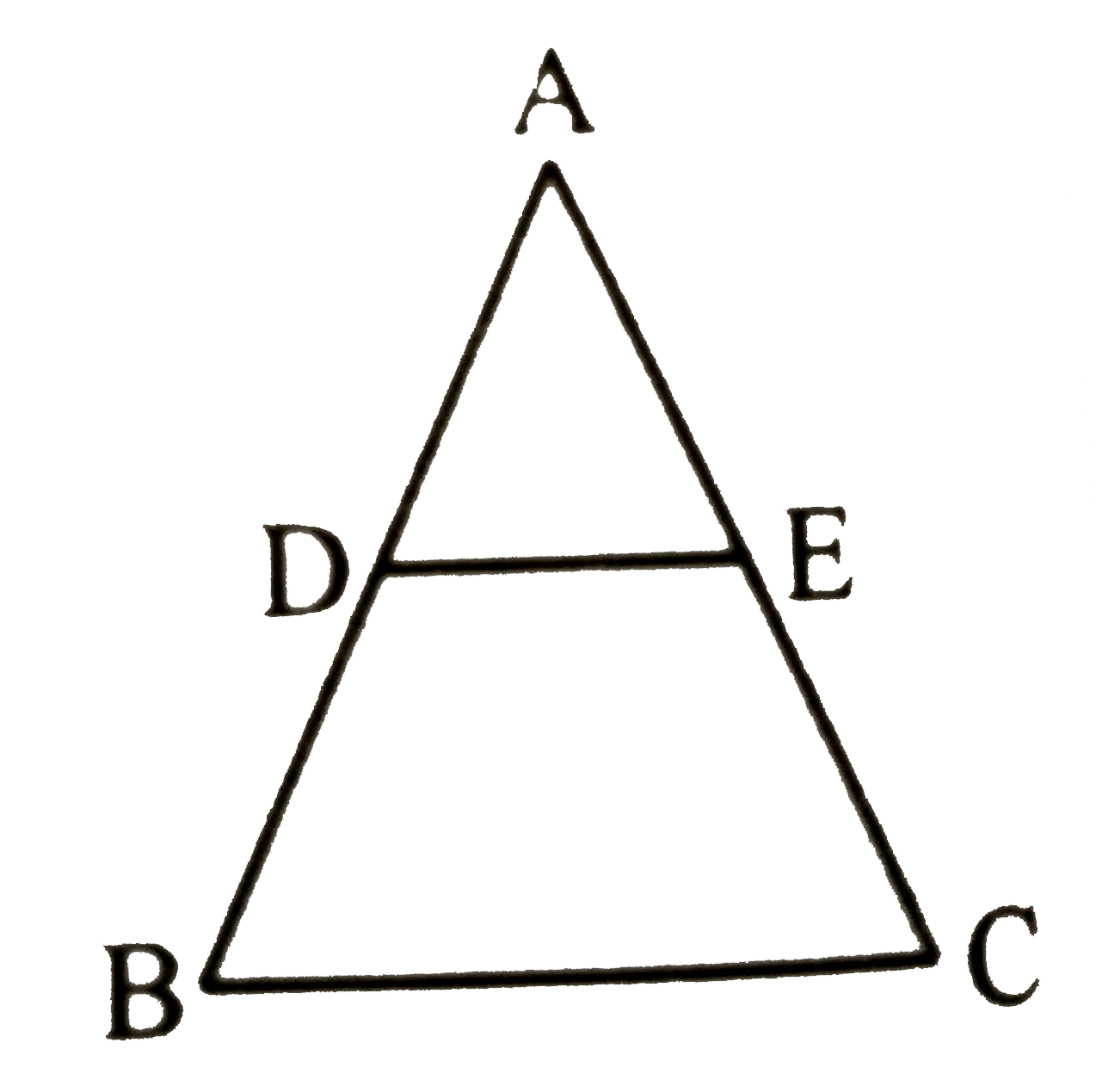
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
 03:02View Solution
03:02View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |
 04:00View Solution
04:00View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
03:47View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
01:57View SolutionIn a ABC, AD⊥BC and AD2=BD×CD. Prove that ABC is a right triangle.
03:27View SolutionIn a ABC, AD⊥BC and AD2=BD×CD. prove that ABC is a right triangle.
05:59View Solutionमाना कि एक त्रिभुज ABC है जिसमे ∠A=90∘ तथा AD⊥BC तो सिद्ध कीजिए कि AD2=BD⋅CD
05:03View SolutionIn Δ ABC , AD ⊥BC and AD2=BD×CD. Prove that AB2+AC2= (BD+CD)2
 04:28View Solution
04:28View Solution△ABC ಯಲ್ಲಿ AD⊥BC ಮತ್ತು AD2=BDxCD ಆಗಿದೆ. ಹಾಗಾದರೆ AB2+AC2=(BD+CD)2 ಎಂದು ಸಾಧಿಸಿ.
 06:35View Solution
06:35View SolutionΔABC లో AD⊥BC మరియు AD2=BD∗CD అయిన త్రిభుజము ABC లంబకోణ త్రిభుజామని చూపుము.
 03:22View Solution
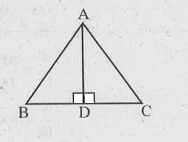
03:22View SolutionIn an isosceles triangle ABC with AB = AC and AD is perpendicular to BC, if AD = 6 cm and the perimeter of triangle ABC is 36 cm, then the area of triangle ABC is: एक समद्विबाह त्रिभुज ABC में AB=AC और AD, BC पर लंबवत है, यदि AD = 6 सेमी और ABC की परिधि 36 सेमी है, तो ABC का क्षेत्रफल है
02:19View SolutionIn an isosceles triangle ABC, AB=AC and AD is perpendicular to BC at D. If AD = 8 cm and perimeter of triangle ABC is 64cm, then the area of triangle ABC एक समद्विबाहु त्रिभुज ABC में, AB= AC और AD, BC पर लंबवत है। यदि AD =8 सेमी और ABC की परिधि 64 cm है, तो ABC का क्षेत्रफल है:
02:11View SolutionIn triangle ABC , AD bot BC and BE bot AC , AD and BE intersect each other at F. If BF = AC, then the measure of angle ABC is: त्रिभुज ABC में, AD bot BC है तथा BE bot AC है | AD और BD एक दूसरे को F पर काटते है | यदि BF = AC है, तो angle ABC का माप क्या होगा ?
05:35View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
06:37View SolutionIn triangle ABC , AD is the median and G is a point on AD such that AG : GD = 2 : 1, then ar (triangle BDG): (triangle ABC) is equal to : त्रिभुज ABC में, AD माध्यिका है तथा G, AD पर ऐसा बिंदु है कि AG : GD = 2 : 1 है, तो ar (triangle BDG): (triangle ABC) का मान ज्ञात करें |
04:12View Solution