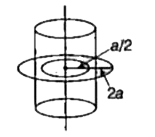
त्रिज्या a के किसी लम्बे सीधे तार में कोई अस्थायी धारा i प्रवाहित हो रही ही। इस तर की अनुपृष्ठ-काट पर धारा एकसमान रूप से वितरित है। तार की अक्ष से त्रिज्या दूरियों a/2 तथा 2a पर क्रमशः चुंबकीय क्षेत्र B1 तथा B2 का अनुपात है:
1/2
1
4
1/4
The correct Answer is:B
जैसा कि चित्र में दिखाया गया है, त्रिज्या a2 तथा 2a के दो ऐम्पियर लूपों पर विचार
करें। इन लूपों के लिए ऐम्पियर का परिपथीय नियम लगाने पर हम पाते हैं।
∮B.dL=μ0Iबंद
छोटे लूप के लिए,
⇒B×2πa2=μ0×Iπa2×π(a2)2
=μ0I×14=μ0I4
⇒B.=μ0I4πa
तार के अक्ष से a2 दूरी पर।
इसी तरह बन्द लूप के लिए,
B×2π(2a)=μ0I
(ऐम्पियर लूप के द्वारा कुल बन्द धारा I है) तार के अक्ष से 2a दूरी पर,
⇒B.=μ0I4πa अत: अनुपात, BB.=μ0I4πa×4πaμ0I=1
Related Playlists
- BOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश और चुम्बकत्वEXERCISE - NCERT पर based Objective प्रश्न ( टॉपिक 4 धारा लूप तथा चुम्बकीय द्विध्रुव पर बल आघूर्ण (Torque on Current Loop and Magnetic Dipole) )19videos
गतिमान आवेश और चुम्बकत्व
- BOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश और चुम्बकत्वEXERCISE - NCERT पर based Objective प्रश्न ( टॉपिक 5 चल कुण्डली गैल्वेनोमीटर (Moving Coil Gavanometer) )22videos
गतिमान आवेश और चुम्बकत्व
- BOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश और चुम्बकत्वEXERCISE - NCERT पर based Objective प्रश्न ( टॉपिक 2 संयुक्त विद्युत तथा चुम्बकीय क्षेत्रों में गति (Motion in combined Electric and Magnetic Field )13videos
गतिमान आवेश और चुम्बकत्व
- BOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश एवं चुम्बकीय क्षेत्र EXERCISE - MCQs54videos
गतिमान आवेश एवं चुम्बकीय क्षेत्र
- BOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश तथा चुम्बकत्व EXERCISE - बहुविकल्पीय प्रश्न71videos
गतिमान आवेश तथा चुम्बकत्व
Similar Questions
10 सेमी तथा 5 सेमी भुजाओं के एक आयताकार लूप से एक विद्युत धारा I=12 ऐम्पियर, प्रवाहित हो रही है। इस लूप को आरेख में दर्शाए गए अनुसार विभिन्न अभिविन्यासों (स्थितियों) में रखा गया है।
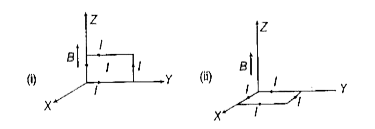
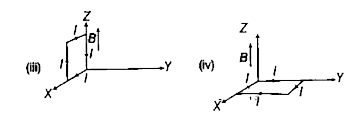
यदि वहाँ 0.3 टेस्ला तीव्रता का कोई एकसमान चुम्बकीय क्षेत्र धनात्मक Z−दिशा में विद्यमान है, तो दर्शाए गए किस अभिविन्यार में, यह लूप स्थायी सन्तुलन तथा अस्थायी सन्तुलन में होगा?02:48View Solutionचल कुण्डली गैल्वेनोमीटर एक ऐसा यन्त्र है, जो
02:29View Solutionदिए गए चित्र में E एवं B विद्युत क्षेत्र एवं चुम्बकीय क्षेत्र के परिमाण हैं। विद्युत एवं चुम्बकीय क्षेत्र एक-दूसरे के लम्बवत् हैं, जो एक गतिशील इलेक्ट्रॉन पर कार्य कर रहे हैं। इलेक्ट्रॉन का वेग X-अक्ष के अनुदिश है। इलेक्ट्रॉन पर बल है।
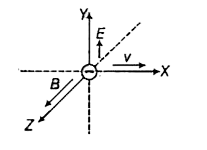 06:20View Solution
06:20View Solutionकिसी चल कुण्डली गैल्वेमीटर की धारा सुग्रहिता 5div/mA और वोल्टता सुग्राहिता ( प्रयुक्त इकाई वोल्टता से उत्पन्न कोणीय विक्षेप ) 20div/V है। इस गैल्वेमीटर का प्रतिरोध है
04:06View Solutionएक धारा प्रवाहित कुण्डली एक समान चुम्बकीय क्षेत्र में रखी गयी है। कुण्डली घूमेगा ताकि उसका समतल
05:40View Solutionएक लम्बे सीधे तार में बहने वाली धारा 1 ऐम्पियर है। चुंबकीय क्षेत्र की तीव्रता 10−5 वेबर/मीटर2 होगी तार से :
02:42View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
41:43View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
46:59View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
07:31View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
40:12View Solutionसीधे चालक से विद्युत् धारा प्रवाहित होने के कारण चुंबकीय क्षेत्र
33:44View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है36:10View Solutionसीधे धारावाही चालक तार के कारण किसी बिन्दु पर चुंबकिय क्षेत्र की तीव्रता
01:22:10View SolutionAmpere has given a theory to find the magnetic field due to current distribution. in loop धारा I_(3) के चुम्बकीय क्षेत्र में अंशदान को नहीं लेते है क्योंकि चुम्बकीय क्षेत्र पुरे लूप मे युग्मित है। एक समाक्षीय केबिल में तार की त्रिज्या a है , इसके चारो ओर के बेलनाकार सेल की आंतरिक व बाह्य त्रिज्याएँ क्रमशः b तथा c है। अंदर वाले तार में i ऐम्पियर धारा बहती है तथा बाहरी सेल में बराबर व विपरीत धारा बहती है। अक्ष से x दूरी ( x lt a) पर चुंबकीय क्षेत्र है
43:47View Solutionधारावाही तार पर चुंबकीय क्षेत्र मे बल
01:22:56View Solution


