दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलो वाले चार त्रिभुजों के बाँटते है ।
Step by step video & image solution for दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलो वाले चार त्रिभुजों के बाँटते है । by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
- BOOK - NCERT HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.48videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NCERT HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.26videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NCERT HINDICHAPTER - संख्या पद्धतिEXERCISE - प्रश्नावली 1.63videos
संख्या पद्धति
- BOOK - NCERT HINDICHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 14.46videos
सांख्यिकी
Similar Questions
समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है । दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है ।
45:28View Solutionआकृति में, ABCD एक समांतर चतुर्भुज है, AE⊥DC और CF⊥AD है। यदि AB=16cm,AE=8cm और CF=10cm है, तो AD ज्ञात कीजिए।
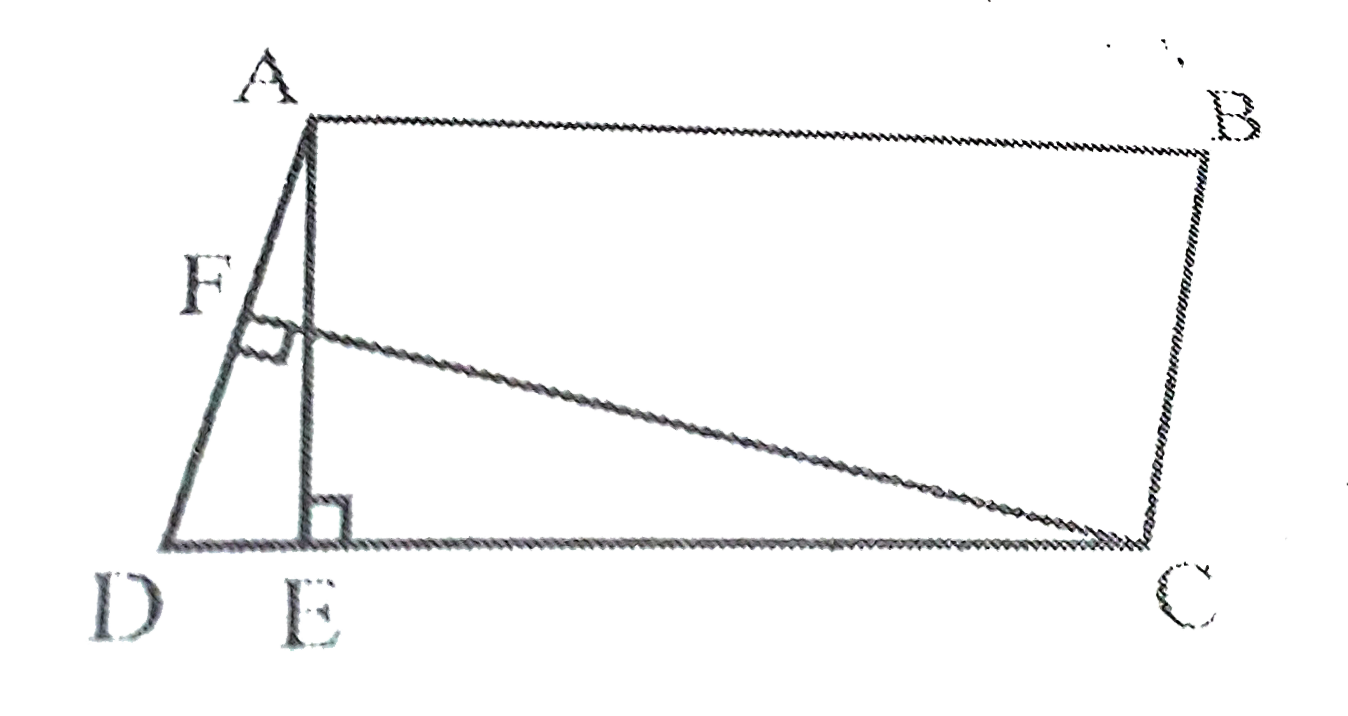 37:14View Solution
37:14View Solutionज्ञात कीजिए : (i) 6412 (ii)3215 (iii)12513
38:34View Solutionएक टीम ने फुटबॉल के 10 मैचों में निम्नलिखित गोल किएः
2, 3, 4, 5, 0, 1, 3, 3, 4, 3
इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए:42:18View SolutionRevision|समांतर चतुर्भुज के गुण
40:07View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
41:15View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
34:48View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
35:27View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
40:54View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
41:42View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
36:35View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
51:39View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल के महत्वपूर्ण प्रश्न
29:12View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
39:33View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
36:27View Solutionचतुर्भुज |चतुर्भुज का कोण योग गुण |चतुर्भुज के प्रकार |समांतर चतुर्भुज के गुण|प्रमेय|सारांश
34:53View Solution


