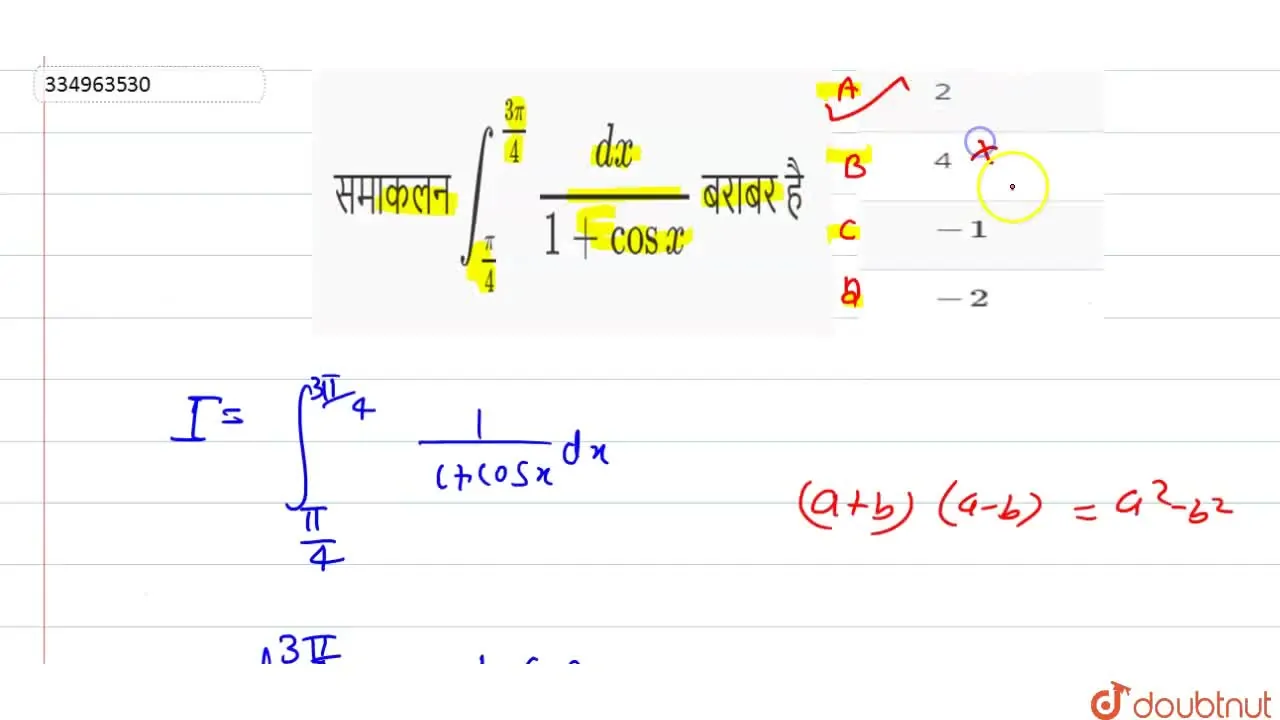
समाकलन बराबर है
2
4
The correct Answer is:a
Step by step video, text & image solution for समाकलन int_(pi/4)^((3pi)/4)(dx)/(1+cosx) बराबर है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
एक अऋणात्मक पूर्णांक a जिसके लिए निम्न limx→1{−ax+sin(x−1)+ax+sin(x−1)−1}1−x1−√x=14 सत्य है तो a का अधिकतम मान है।
05:21View Solutionमाना [t] महत्तम पूर्णांक ≤t है। जहाँ फलन f(x)=[x]∣∣x2−1∣∣+sin(π[x]+3)−[x+1],x∈(−2,2) संतत नहीं है, ऐसे बिन्दुओं की संख्या है
03:57View SolutionThe value of the integral ∫5π/4−3π/4(sinx+cosx)ex−π/4+1dx is
05:19View Solution∫3π/4π/4dx1+cosx is equal to
04:39View Solution∫3π/4π/4dx1+cosx is equal to
03:08View Solutionसिद्ध कीजिए कि ∫3π/4π/411+cosxdx=2
02:13View Solution∫3π/4π/411+cosxdx=
03:08View SolutionThe value of ∫3π4π4dx1+cosx is -
02:18View Solution∫3π/4π/411+cosxdx
04:15View Solutionমান নির্ণয় করো:∫3π4π4dx1+cosx
07:06View SolutionThe integral ∫3π4π4dx1+cosx is equal to
04:41View SolutionThe Integral ∫3π4π4dx1+cosx is equal to:
03:00View SolutionThe value of the integral ∫5π/4−3π/4(sinx+cosx)ex−π/4+1dx is
05:33View SolutionThe Integral ∫3π4π4dx1+cosx is equal to: (2) (3) (4)
03:46View Solution∫3π/4π/4dx1+cosx is equal to
04:43View Solution