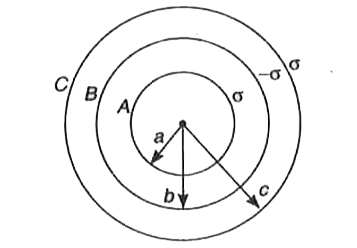
धातु की तीन संकेन्द्री गोलीय कोशों A, B व C की त्रिज्यायें a, b व c (a<b<c) हैं तथा इनके आवेशों के पृष्ठ घनत्व क्रमशः σ,−σ व σ हैं। (a) तीनों गोलीय कोशों 4, B व C के विभव ज्ञात कीजिए। (b) यदि कोश A व C समान विभव पर हैं तो त्रिज्याओं a, b व c में सम्बन्ध ज्ञात कीजिए।
The correct Answer is:(a) VA=σε0(a−b−+c),Ve=σε0(a2b−b+c)
VC=σε0(a2c−b2c+c)
a+b=c
(a) किसी भी कोश पर विभव तीनो आवेशों के कारण होगा।
VA=14πε0[qAa+qBb+qCc)]
=14πε0[(4πa2)(σ)a+(4πb2)(−σ)b+(4πc2)(σ)c)]
=σε0(a−b+c)
VB=(14πε0[qAb+qBb+qCc)]
=14πε0[(4πa2)(σ)b+(4πb2)(−σ)b+(4πc2)(σ)c)]
=σε0[a2b−b+c]
इसी प्रकार VC=14πε0[qAc+qBc+qCc]
=14πε0[(4πa2)(σ)c+(4πb2)(−σ)c+(4πc2)(σ)c]
=σε0[a2c−b2c+c]
(b) दिया है, VA=VC
σε0(a−b+c)=σε0(a2c−b2c+c)
a−b+c=a2c−b2c+c
⇒a+b=c
Related Playlists
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार3videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार4videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्व्ड पेपर 2017 JEE ADVANCEDEXERCISE - पेपर 2(खण्ड-3)4videos
सॉल्व्ड पेपर 2017 JEE ADVANCED
Similar Questions
नाभिकीय आवेश (Ze), R त्रिज्या वाले नाभिक के भीतर असमान रूप से वितरित रहता हैं। आवेश घनत्व p(r) (अर्थात् एकांक आयतन में आवेश की मात्रा) नाभिक के केन्द्र से त्रिज्य दूरी (r) पर ही निर्भर करता है। वैद्युत क्षेत्र त्रिज्य दिशा के अनुदिश है।
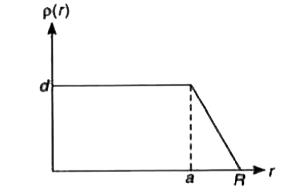
दूरी r= R पर वैघुत क्षेत्र है।View Solutionत्रिज्या R के एक ठोस गोले के सम्पूर्ण आयतन में आवेश Q को इस प्रकार बाँटा गया है कि आवेश-घनत्व p=kra है। यहाँ k तथा a व नियतांक हैं तथा r गोले के केन्द्र से दूरी है। यदि इस गोले में r=R2 पर विद्युत का मान r= R पर विद्युत क्षेत्र के मान का 18 है, तो नियतांक a का मान निकालें।
04:39View Solutionएक साधारण RC परिपथ को देखिए, जैसा चित्र 1 (Figure 1) में दर्शाया गया है। प्रक्रम 1 (Process1) t= 0 पर स्विच S द्वारा परिपथ पूर्ण किया जाता है एवं संधारित्र पूर्ण रूप से वोल्टता V0 से आवेशित हो जाता है। (T» RC समय तक आवेषण चलता रहता है। इस प्रक्रम में प्रतिरोध के द्वारा कुछ विद्युत-कर्जा क्षय (energy dissipated) ED होती है। पूर्ण रूप से आवेशित संधारित्र में संचित ऊर्जा (stored energy in a charged capacitor) का मान EC है।
Q प्रक्रम 1, में संधारित्र में संचित ऊर्जा EC और प्रतिरोध R द्वारा ऊर्जा क्षय E0में सम्बनध है।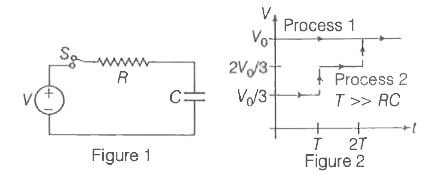 01:38View Solution
01:38View Solutionयदि बिन्दु B तथा C पर ताप क्रमश:T1वT2 , हों तो-
06:58View SolutionMnO2,H2S2O8,KMnO_4वCH_2Cl_2 में क्रमशः Mn , S, Mn व C के ऑक्सीकरण अंक लिखिए।
09:29View Solutionx,y व z के किन मानो के लिए आव्यूह A व B समान आव्यूह है , जहाँ A=[0−1x+2y−345],B=[0−17−24z]
02:57View Solutionयदि द्विघात समीकरण (b−c)x2+(c−a)x+(a−b)=0 के मूल वास्तविक व बराबर हो तो सिद्ध कीजिये की 2b=a+c
04:05View Solutionएक न्याय्य पासे को उछला गया है। घटनाओं A={1,3,5}, B={2,3} व C={2,3,4,5} के लिए निम्नलिखित ज्ञात कीजिये - (i) P(AB) व P(BA), (ii) P(AC) व P(CA) (iii)P(A∪BC) व P(A∩BC)
02:53View Solutionयदि loge(a+b2)=12(logea+logeb), तब a व b, के मध्य सम्बन्ध होगा।
11:38View Solutionयदि (1+ax)n,(n≠0) के प्रसार में प्रथम तीन पद क्रमशः 1,6x व 16x2 हों, तो a व n का मान होगा
43:52View Solutionएक कण पर लगे समान परिमाण वाले तीन बल संतुलन में हैं, तो उनके बीच व कोण _____ होगा।
01:00:05View Solutionतीन संकेद्रीय गोलीय कोश की त्रिज्याएँ a, b व c(a<b<c) हैं तथा इनके आवेश पृष्ठ घनत्व क्रमशः σ,−σवσ हैं | यदि VA,VBवVC तीनों गोलीय कोश के विभव हों , तब c = a + b , के लिये है
47:57View Solutionकुलाम्ब के नियम व आवेशों की साम्यावस्था पर आधारित प्रश
44:26View Solutionथायरॉइड व पैरा थायरॉइड ग्रंथि की संरचना व कार्य | Ca व Fe का रक्त में नियमन
43:00View Solutionपैरा थाइरॉइड ग्रंथि के विवरण व कार्य | एड्रिनल ग्रंथि के कार्य व विवरण व सिद्धांत की चर्चा
42:44View Solution


