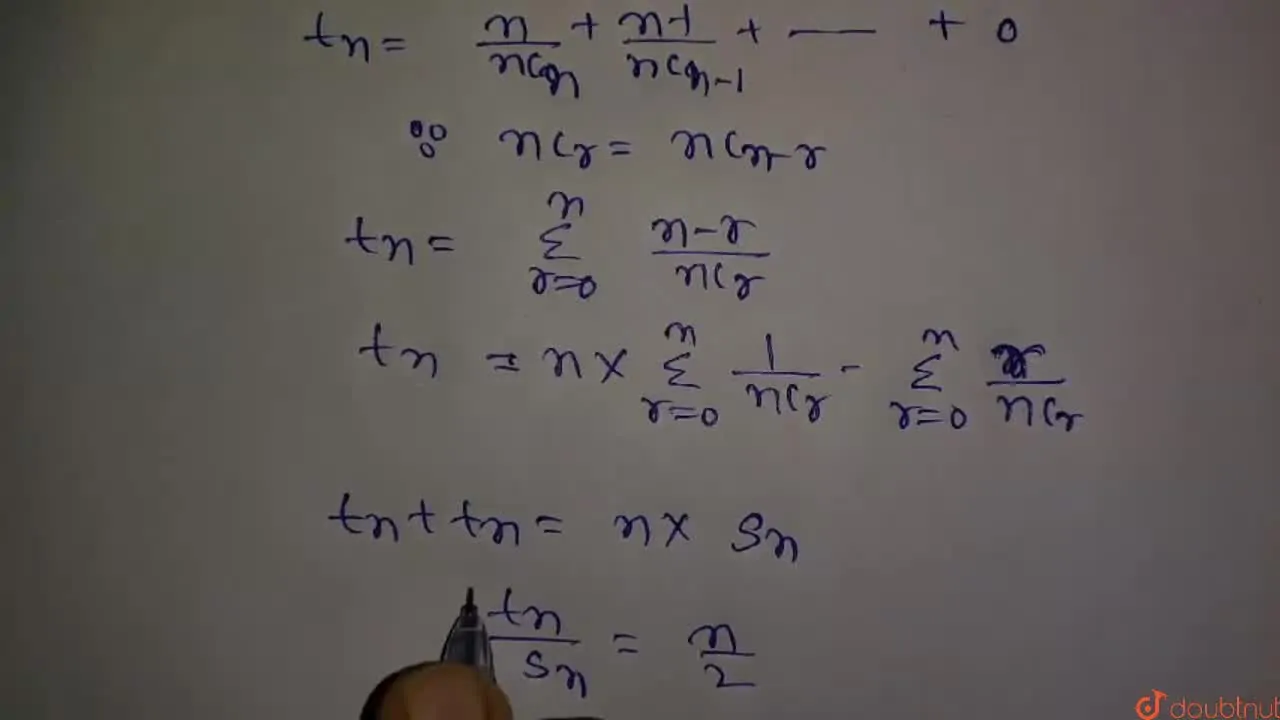यदि sn=n∑r=01.nCr तथा तो tn=n∑r=0r.nCr, तो tnsn=....है :
12n
12n−1
n−1
12(2n−1)
The correct Answer is:A
Step by step video, text & image solution for यदि s_(n) = sum_(r=0)^(n)1/(.^(n)C_(r))" तथा तो " t_(n) = sum_(r =0)^(n) r/(.^(n)C_(r))," तो " t_(n)/s_(n) =....है : by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - द्विपद प्रमेय EXERCISE - बहु-विकल्पीय प्रश्न (वस्तुनिष्ठ प्रश्न)21videos
द्विपद प्रमेय
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - द्विपद प्रमेय EXERCISE - रिक्त स्थान पूर्ति11videos
द्विपद प्रमेय
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - द्विपद प्रमेय EXERCISE - वस्तुनिष्ठ प्रश्न ( एक शब्द / वाक्य में उत्तर )13videos
द्विपद प्रमेय
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - त्रिविमीय ज्यामितिEXERCISE - एक शब्द/वाक्य में उत्तर3videos
त्रिविमीय ज्यामिति
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - द्विविमीय ज्यामिति का संक्षिप्त पुनरावलोकन EXERCISE - बहुविकल्पीय प्रश्न14videos
द्विविमीय ज्यामिति का संक्षिप्त पुनरावलोकन
Similar Questions
(a+b)n के प्रसार में मध्य पद होगा जबकि n सम हो-
06:22View Solution(3x+2y)11 के प्रसार में पदों की संख्या……………….है।
02:34View Solution(x+a)n के प्रसार में (r+1) वाँ पद क्या होगा ?
02:45View Solutionबिंदुओं (1,4,5) और (2,2,3) के बीच की दूरी लिखिए।
03:57View Solutionबिंदुओं P(2,7),Q(4,−1),R(−2,6) के संयोजन से बना त्रिभुज है :
03:24View SolutionIf S_(n)=sum_(r=0)^(n)(1)/(nC_(r)) and sum_(r=0)^(n)(r)/(nC_(r)), then (t_(n))/(S_(n))=
03:37View Solutionयदि Sn=n∑r=01nCr और tn=n∑r=0rnCr तब t_(n)/s_(n) =
02:09View SolutionIf an=n∑r=01nCr , find the
value of n∑r=0rnCr04:03View SolutionIf sn=n∑r=01.nCrandtn=n∑r=0r.nCr, then tnsn is equal to
03:14View SolutionIf Sn=n∑r=01nCr and Tn=n∑r=0rnCr then tnsn =
02:31View SolutionIf sn=n∑r=01nCr and tn=n∑r=0rnCr,then tnsn is equal to
03:06View SolutionLet tr=r! and Sn=n∑r=1tr,(n>10) then remainder when Sn is divided by 24 is:
View Solutionयदि an=n∑r=01nCr, तब n∑r=0rnCr का मान है
View SolutionIf an=n∑r=01nCr then n∑r=0rnCr equal to
03:17View SolutionIf an=n∑r=01nCr , find the
value of n∑r=0rnCr03:06View Solution