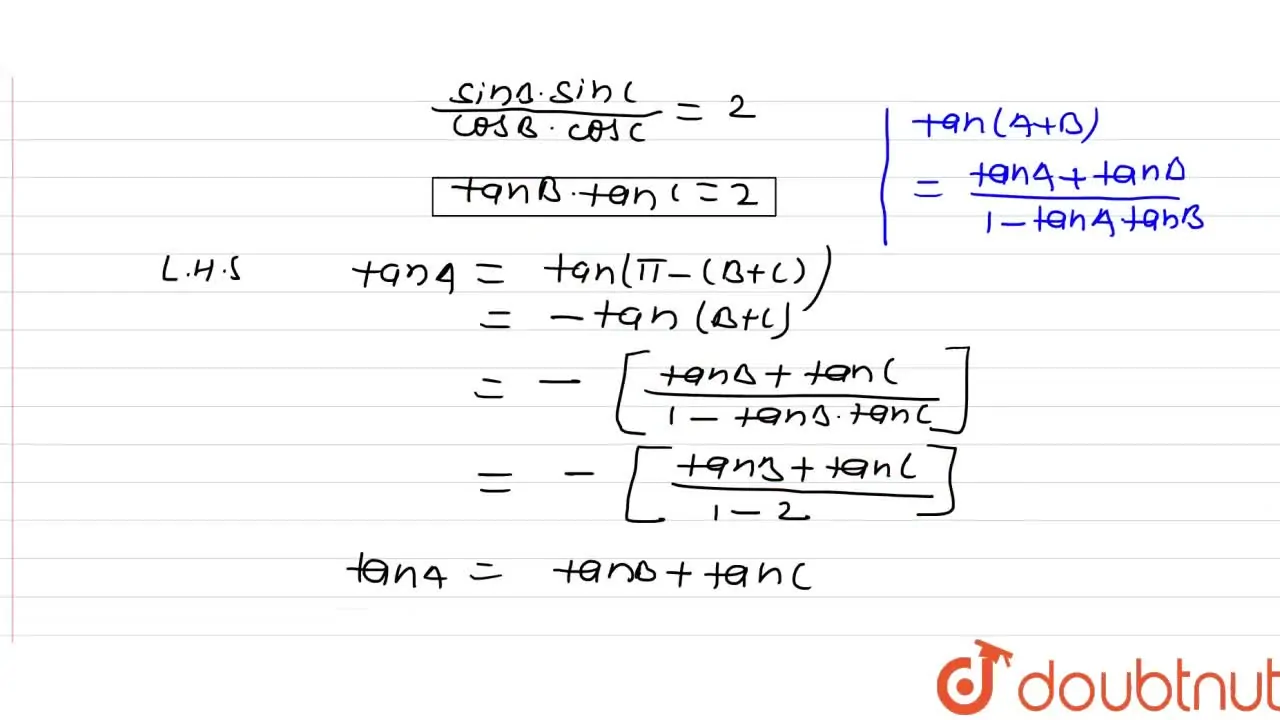
अगर A+B+C=π और cosA=cosB⋅cosC, तो सिद्ध कीजिय की tanA=tanB+tanC.
Step by step video & image solution for अगर A+B+C=pi और cos A = cos B * cos C, तो सिद्ध कीजिय की tan A = tan B + tan C. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - DAS GUPTACHAPTER - संयुक्त कोणों के त्रिकोणमितीय फलन EXERCISE - प्रशनावली 350videos
संयुक्त कोणों के त्रिकोणमितीय फलन
- BOOK - DAS GUPTACHAPTER - संयुक्त कोणों के त्रिकोणमितीय फलन EXERCISE - प्रशनावली 441videos
संयुक्त कोणों के त्रिकोणमितीय फलन
- BOOK - DAS GUPTACHAPTER - शंकु एवं शंकु-परिच्छेदEXERCISE - शंकु-परिच्छेद पर विविध प्रश्न7videos
शंकु एवं शंकु-परिच्छेद
- BOOK - DAS GUPTACHAPTER - समान्तर एवं गुणोत्तर अनुक्रम और श्रेणी EXERCISE - अनुक्रम और श्रेणी पर विविध प्रश्न37videos
समान्तर एवं गुणोत्तर अनुक्रम और श्रेणी
Similar Questions
सिद्ध कीजिय की cos15∘=√3+12√2
01:24View Solutionसिद्ध कीजिए की sin4θ−sin2θ=2cos3θ⋅sinθ.
04:47View Solutionवृत्त x2+y2−2x−2y=0 में अंतरित समद्विबाहु ΔABC में AB = AC है और भुजा BC का समीकरण y = 2x है तो शीर्ष A के नियामक ज्ञात करें।
07:13View Solutionएक अनुक्रम इस प्रकार परिभाषित है-
1=a1=a2 और an=an−1+an−2,n>2.
an+1an निकालें जबकि n=1,2,3,4,5.07:17View SolutionIf A+B+C=pi and cos A=cos B cos C then tan B tan C is equal to
02:41View Solutiontan A ++ tan B + tan C- (sin (A + B + C)) / (cos A cos B cos C) =
03:01View SolutionIn a Delta ABC, if cos A cos B cos C=(1)/(3) then value of,tan A tan B+tan B tan C+tan C tan A is
02:32View SolutionIn Delta ABC If cos A cos B cos C=(1)/(3) then tan A tan B+tan B tan C+tan C tan A=
07:13View SolutionIf cos2B=(cos(A+C))/(cos(A-C)), then tan A,tan B,tan C are in
02:16View SolutionIn a triangle ABC , if cos A = cos B cos C , what is the value of tan A- tan B - tan C ?
03:21View SolutionIf A+B+C=π & cos A = cos B . Cos C then tan B . Tan C has the value equal to
03:51View SolutionIn Delta ABC, if tan ""(A)/(2), tan""(B)/(2) , tan""(C)/(2) are in A.P. then cos A , cos B , cos C are in
05:47View SolutionIfA+B+C=π and cosA=cosBcosC,show that
tanA=tanB+tanC05:25View SolutionA+B+C=π2, A, B, C లలో ఏ ఒక్కటీ π2కి బేసి గుణీజం కాకపోడే tanAtanB+tanBtanC+tanCtanA=1 అని చూపి, దాని నుంచి ∑cos(B+C)cosBcosC=2 అని చూపండి.
03:44View SolutionIf A+B +C = pi And cosA = cos B cos C If so tan B tan C The value of
02:24View Solution