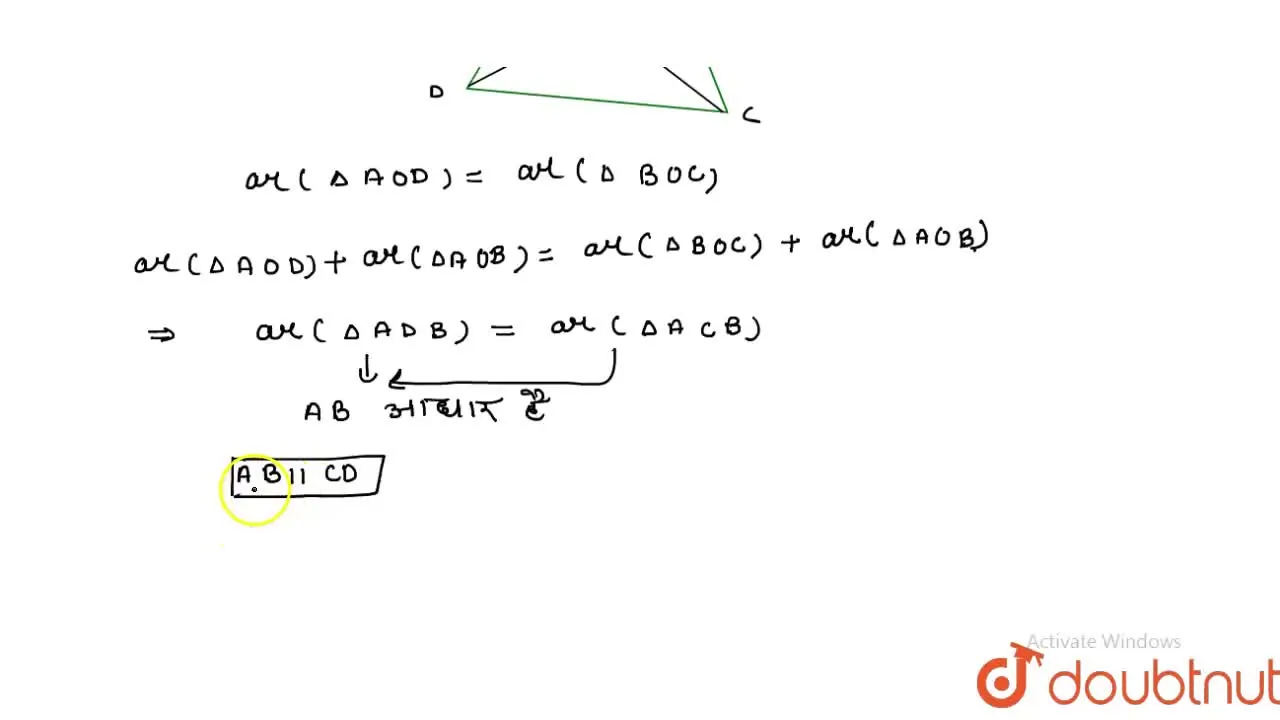
एक चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि ar(AOD) = ar(BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब है।
दिया है कि ABCD एक चतुर्भुज है, जिसके विकर्ण AC और BD एक-दूसरे को O पर प्रतिच्छेद करते है।
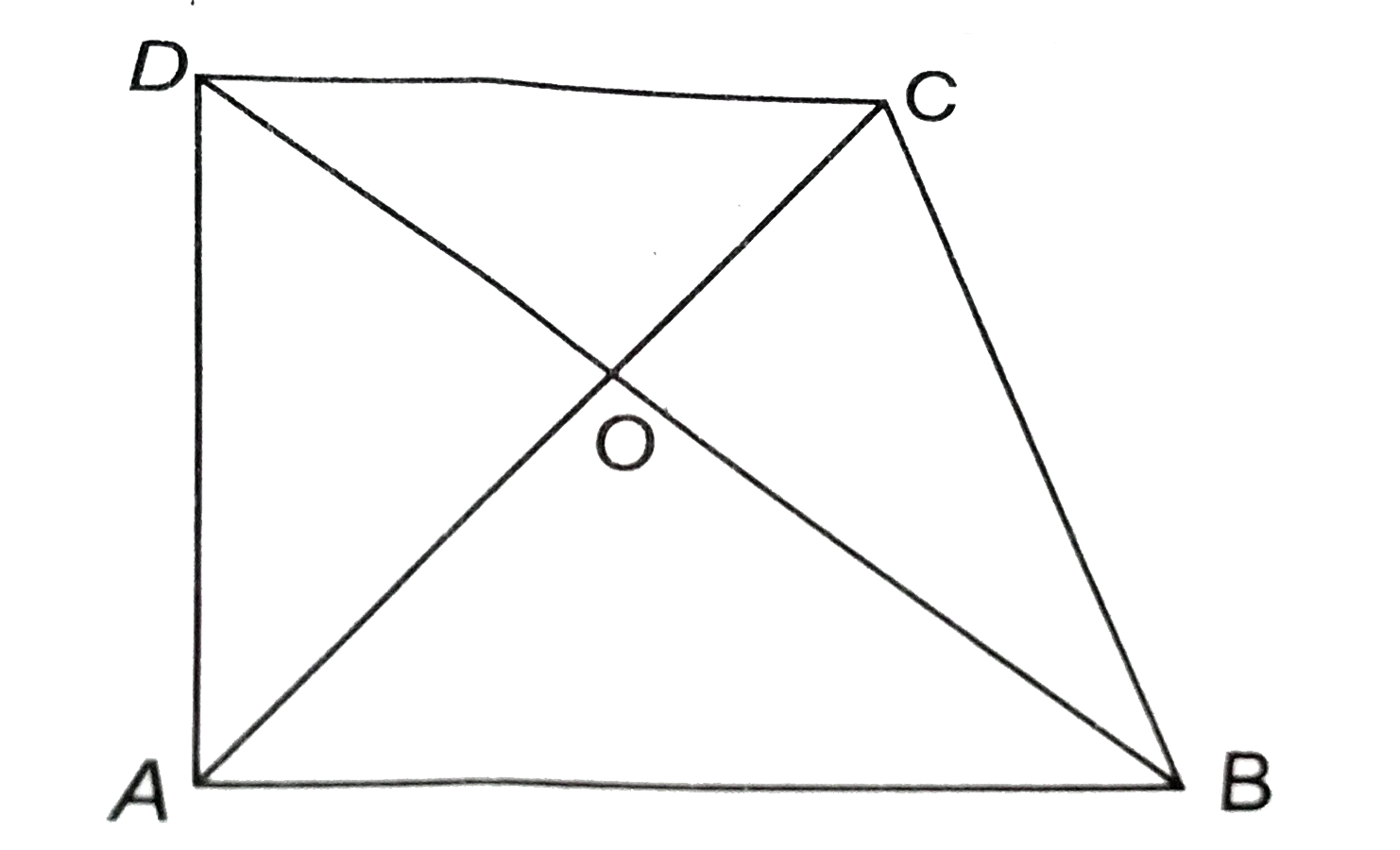
तथा ar(ΔAOD)=ar(ΔBOC)
दोनों पक्षों में ar(ΔAOB) जोड़ने पर
ar(ΔAOD)+ar(ΔAOB)=ar(ΔBOC)+ar(ΔAOB)
⇒ar(ΔADB)=ar(ΔACB)
अब ΔACB और ΔADB समान आधार AB पर स्थित है
और ar(ΔADB)=ar(ΔACB)
अतः ΔACB और ΔADB समान समान्तर रेखाओं के बीच स्थित है।
∴ AB || DC
अतः ABCD एक समलम्ब है।
Related Playlists
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.48videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अतिलघु उत्तरीय प्रश्न10videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.26videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली24videos
चतुर्भुज
Similar Questions
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप आयत के परिमाप से अधिक है।
05:52View Solutionएक समचतुर्भुज के विकर्णों की लम्बाईयाँ 12 सेमी और 16 सेमी है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
02:23View Solutionआकृति में, ABCD एक समान्तर चतुर्भुज है, AE⊥DC और CF⊥AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm है, तो AD ज्ञात कीजिए।
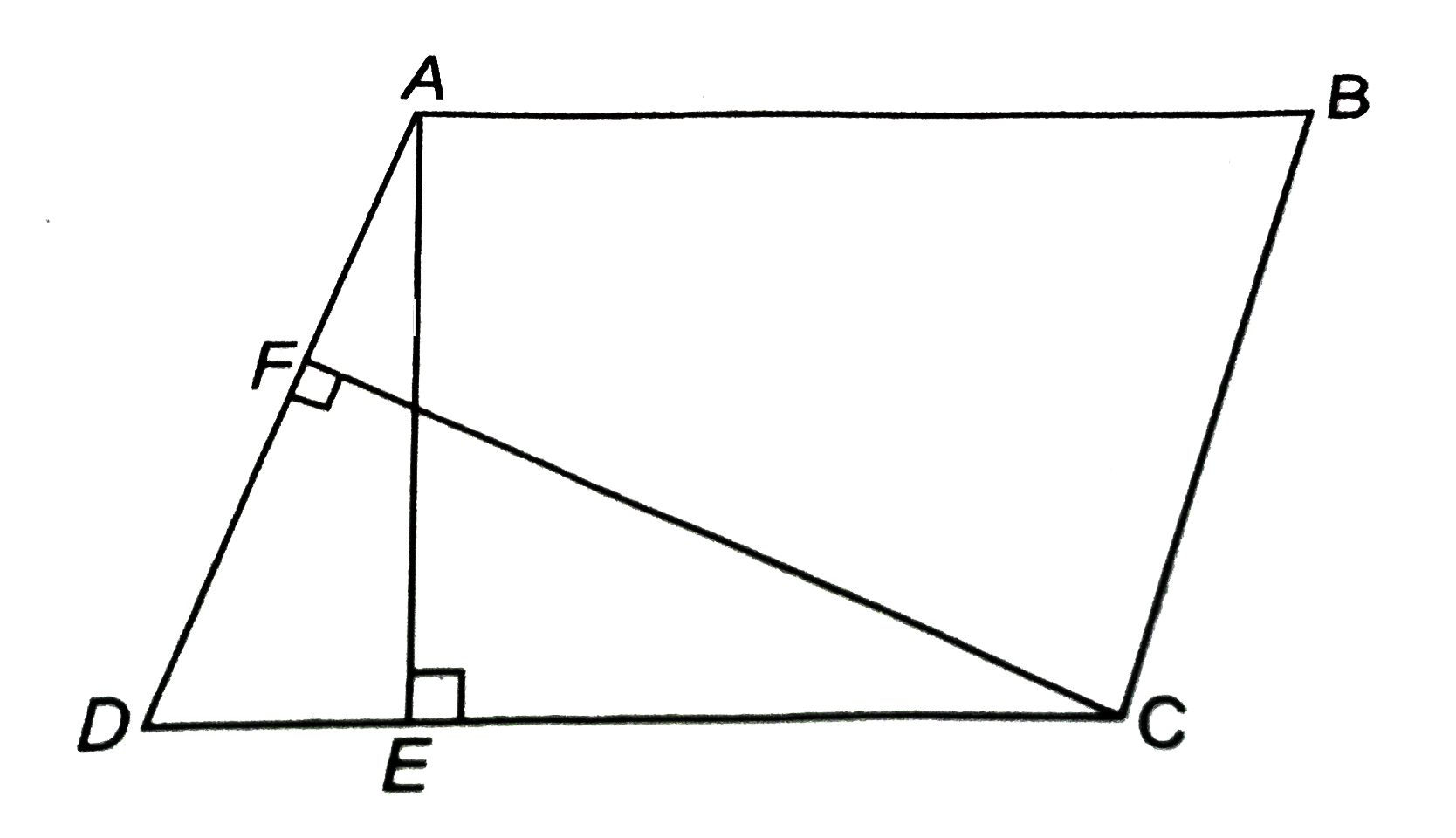 03:08View Solution
03:08View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
02:14View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
05:52View SolutionDiagonals AC and BD of a trapezium ABCD with ABCD intersect each where at O. Prove that ar (AOD)=ar(BOC).
03:22View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
04:11View Solutionएक समलंब ABCD , जिसमें AB ।। DC है , के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते है । दर्शाइए कि ar(AOD)=ar(BOC) है
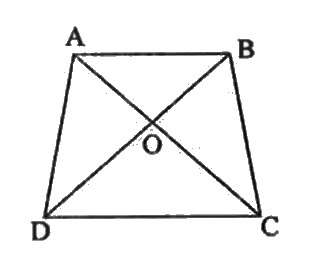
06:40View Solutionचतुर्भुज ACBD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते है कि ar(AOD)=ar(BOC) है सिद्ध कीजिए कि ABCD एक समलंब है
02:42View SolutionDiagonals AC and BD of a trapezium ABCD with AB∣∣DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
 03:43View Solution
03:43View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
05:05View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
02:37View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
03:35View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
05:04View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
03:27View Solution