एक आयत का परिमाप 130 cm है। यदि आयत की चौड़ाई 30 cm हो तो आयत की लंबाई ज्ञात कीजिए। आयत का क्षेत्रफल भी ज्ञात कीजिए।
The correct Answer is:35 cm; 1050cm2
Step by step video, text & image solution for एक आयत का परिमाप 130 cm है। यदि आयत की चौड़ाई 30 cm हो तो आयत की लंबाई ज्ञात कीजिए। आयत का क्षेत्रफल भी ज्ञात कीजिए। by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Related Playlists
- BOOK - NCERT HINDICHAPTER - परिमाप और क्षेत्रफल EXERCISE - प्रश्नावली 11.28videos
परिमाप और क्षेत्रफल
- BOOK - NCERT HINDICHAPTER - परिमाप और क्षेत्रफल EXERCISE - प्रश्नावली 11.317videos
परिमाप और क्षेत्रफल
- BOOK - NCERT HINDICHAPTER - परिमाप और क्षेत्रफल EXERCISE - इन्हें कीजिए10videos
परिमाप और क्षेत्रफल
- BOOK - NCERT HINDICHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - प्रस्नावली 7.29videos
त्रिभुजों की सर्वांगसमता
- BOOK - NCERT HINDICHAPTER - परिमेय संख्याएँEXERCISE - प्रश्नावली 9.24videos
परिमेय संख्याएँ
Similar Questions
निम्न में प्रत्येक समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
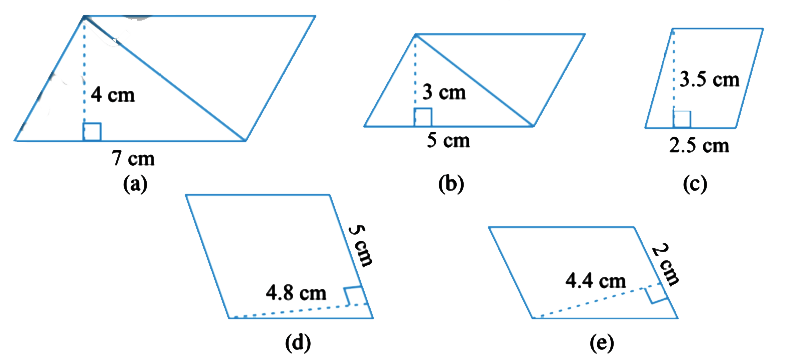 03:15View Solution
03:15View Solutionनिम्न त्रिज्याओं वाले वृत्तों की परिधि ज्ञात कीजिए (π=227 लीजिए।)
(a) 14 cm (b) 28 mm (c) 21 cm02:34View Solutionनीचे दिए गए प्रश्नों के उत्तर देने के लिए आपको क्षेत्रफल या परिमाप में से किसको ज्ञात करने की आवश्यकता होगी।
1. एक श्यापट कितनी जगह घेरता है
2. एक आयताकार फूलों की क्यारी के चारों ओर बाड़ लगाने के लिए आवश्यक तार की लंबाई क्या है?
3. एक तिकोने पार्क के चारों ओर दो बार चक्कर लगाने पर आप कितनी दूरी तय करेंगें? 3. एक आयताकार स्वीमिंग पूल को ढकने लिए आपकों कितनी प्लास्टिक शीट की आवश्यकता होगी?02:58View Solutionनिम्न में आप कौन से सर्वांगसम प्रतिबंधों का प्रयोग करेंगे?
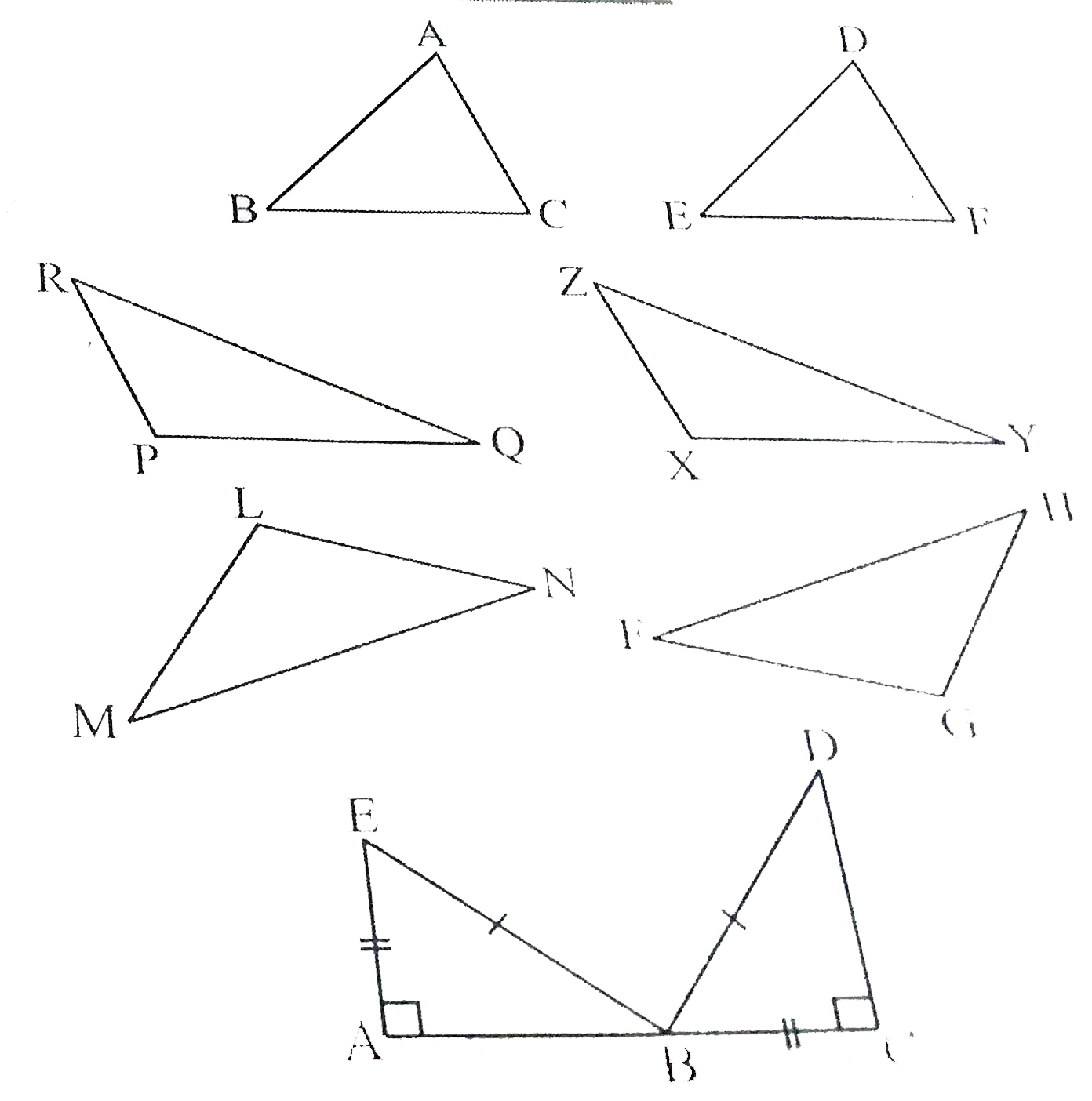 04:03View Solution
04:03View Solutionयोग ज्ञात कीजिए :
(i)54+(−114) , (ii) 53+35 , (iii) −910+2215
(iv) −3−11+59 , (v) −819+(−2)57 , (vi) −23+0
(vii) −2'13+4'3501:28View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
01:42View Solutionएक आयत की लम्बाई x, 5 cm / min की दर से घट रही है और चौड़ाई y, 4 cm / min कि दर से बढ़ रही है जब x=8 cm और y= 6 cm है तब आयत के (a) परिमाप (b) क्षेत्रफल की परिवर्तन की दर ज्ञात कीजिए
01:41View Solutionएक आयत की लम्बाई x, 5 cm / min की दर से घट रही है और चौड़ाई y, 4 cm / min कि दर से बढ़ रही है जब x=8 cm और y= 6 cm है तब आयत के (a) परिमाप (b) क्षेत्रफल की परिवर्तन की दर ज्ञात कीजिए
01:40View SolutionThe perimeter of a rectangle is 50 cm. Its area and length are in the ratio of 5:1. Find the length of the rectangle?
एक आयत की परिधि 50 सेमी है। इसका क्षेत्रफल और लंबाई 5: 1 के अनुपात में है। आयत की लंबाई ज्ञात कीजिये?01:46View SolutionThe length and breadth of a rectangle are in the ratio 5 : 3. If the length is 8 m more than the breadth, what is the area of the rectangle?
एक आयत की लंबाई और चौड़ाई 5: 3 में है। 3. यदि लंबाई चौड़ाई से 8 मीटर अधिक है, तो आयत का क्षेत्रफल क्या है?01:36View SolutionThe length and breadth of a rectangle are in ratio 3:2. If its perimeter is 730 cm, what is the area of the rectangle?
एक आयत की लंबाई और चौड़ाई 3:2 के अनुपात में है। यदि इसकी परिधि 730 सेमी है, तो आयत का क्षेत्रफल क्या है?01:29View SolutionIf the perimeter and length of a rectangle are in the ratio 6:1 and the area of the rectangle is 288cm2. Find the length of the rectangle.
यदि आयत की परिधि और लंबाई 6: 1 के अनुपात में है और आयत का क्षेत्रफल 288 वर्ग सेमी है। आयत की लंबाई ज्ञात कीजिए।01:31View SolutionThe length of the diagonal of a rectangle is 26 cm and one side is 10 cm. The area of the rectangle is:
एक आयत के विकर्ण की लंबाई 26 सेमी है तथा इसकी एक भुजा 10 सेमी की है | इस आयत का क्षेत्रफल है:01:55View SolutionThe diagonal of the rectangle is 15 cm and length is 12 cm. Find the area of the rectangle.
एक आयत का विकर्ण 15 सेमी तथा लंबाई 12 सेमी है। आयत का क्षेत्रफल ज्ञात कीजिए।01:19View SolutionThe perimeter and length of a rectangle are in the ratio of 8:1, and the area of the rectangle is 1323cm2. Find the length of the rectangle.
एक आयत का परिमाप और उसकी लंबाई 8:1 के अनुपात में है। आयत का क्षेत्रफल 1323 वर्ग सेमी है। आयत की लंबाई ज्ञात कीजिए।01:42View SolutionThe breadth of a rectangle is four times of its length. If the area of the rectangle is 1764, then what is the breadth of the rectangle? एक आयत की चौड़ाई इसकी लंबाई का चार गुना है। यदि आयत का क्षेत्रफल 1764 है, तो आयत की चौड़ाई क्या है?
01:28View Solution


