यदि A=[cosθ−sinθsinθcosθ], तो साबित करे कि An=[cosnθ−sinnθsinnθcosnθ], जहाँ n एक धन पूर्णांक है ।
यहाँ हम गणितीय आगमन के सिध्दांत का प्रयोग करेंगे ।
माना कि P(n):An=[cosnθ−sinnθsinnθcosnθ]
जब n=1,L.H.S.=A=[cosθ−sinθsinθcosθ]andR.H.S.=[cosθ−sinθsinθcosθ]
अत: P(1) सत्य है । ...(A)
माना कि P(m) सत्य है ⇒ Am=[cosmθ−sinmθsinmθcosmθ] ...(2)
साबित करना है कि P(m + 1) सत्य है अर्थात
Am+1=[cos(m+1)θ−sin(m+1)θsin(m+1)θcos(m+1)θ] ...(3)
(2) के दोनों पक्षों को आव्यूह A से गुणा करने पर, हमे मिलता है
Am+1=A[cosmθ−sinmθsinmθcosmθ]
=[cosθ−sinθsinθcosθ][cosmθ−sinmθsinmθcosmθ]
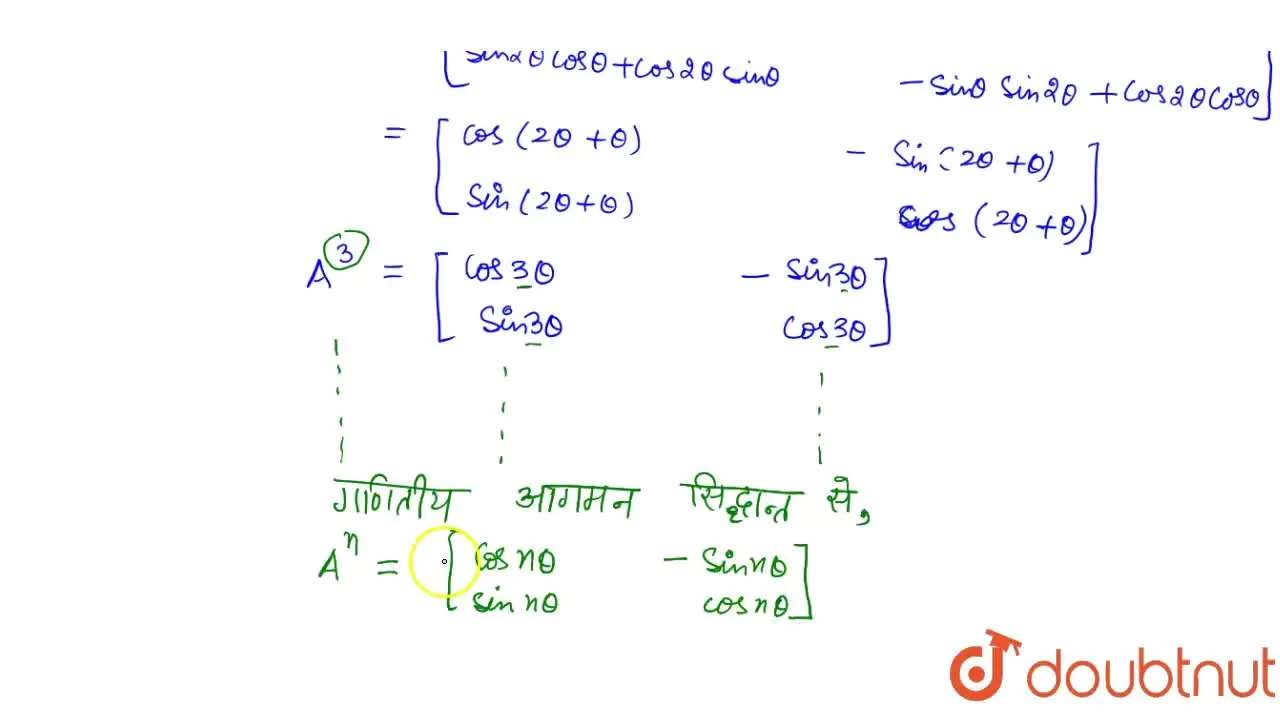
=[cosθcosmθ−sinθsinmθ−cosθsinmθ−sinθcosmθsinθcosmθ+cosθsinmθ−sinθsinmθ+cosθcosmθ]
=[cos(m+1)θ−sin(m+1)θsin(m+1)θcos(m+1)θ]
अत: P(m) सत्य होने पर P(m+1) सत्य है । ...(B)
(A) तथा (B) से, गणितीय आगमन के सिद्धांत से सभी प्राकृत संख्याओं n के लिए P(n) सत्य है ।
Related Playlists
- BOOK - KC SINHACHAPTER - आव्यूहEXERCISE - EXERCISE 5.136videos
आव्यूह
- BOOK - KC SINHACHAPTER - आव्यूहEXERCISE - EXERCISE 5.246videos
आव्यूह
- BOOK - KC SINHACHAPTER - अवकलन EXERCISE - OBJECTIVE QUESTIONS28videos
अवकलन
- BOOK - KC SINHACHAPTER - उच्चतम और निम्नतम EXERCISE - प्रश्नावली 18.169videos
उच्चतम और निम्नतम
Similar Questions
(i) 7 अवयवों वाले आव्यूहों की संख्या है......
(ii) 6 अवयवों वाले आव्यूहों की संख्या है........04:22View Solution(i) यदि A=[235] तथा B=⎡⎢⎣123⎤⎥⎦, AB निकाले ।
(ii) यदि A=[213410] तथा B=⎡⎢⎣1−10250⎤⎥⎦ AB और BA निकाले ।08:48View Solutionयदि y=log{log(logx)}, तब dydx=
06:49View Solutionनिम्नलिखित फलन के सभी स्थानीय उच्चतम मान और न्यूनतम बिंदुओं , यदि कोई हो तो ज्ञात कीजिए तथा संगत उच्चतम और निम्नतम मान भी ज्ञात कीजिए| f(x)=x3−6x2+9x+15
05:51View SolutionIf A=[cosθsinθ−sinθcosθ], then prove that An=[cosnθsinnθ−sinnθcosnθ],n∈N.
11:22View SolutionIf A=[(cos theta, sin theta),(-sin theta, cos theta)] , then prove that A^n=[[cosntheta,sin ntheta],[-sin ntheta,cos ntheta]], n in N
07:46View Solution[(1 + cos theta + i sin theta) / (sin theta + i (1 + cos theta))] ^ (4) = cos n theta + i sin n theta
08:11View Solution(cos theta + i sin theta) ^ (n) = cos n theta + i sin n theta
07:46View SolutionIf A=[cosθisinθisinθcosθ] , then prove by principle of mathematical induction that An=[cosn θisinn θisinn θcosn θ] for all n∈N .
06:18View Solutionयाद A=[cosθsinθ−sinθcosθ] तो दिखाइए कि A=[cosnθsinnθ−sinnθcosnθ]
09:37View Solutionयदि A=[cosθ−sinθsinθcosθ], तब दर्शाओ की An=[cosnθ−sinnθsinnθcosnθ] जहाँ n धनात्मक पूर्णांक है।
08:09View Solutionयदि A=[cosθsinθ−sinθcosθ] हो तो सिद्ध कीजिए कि
An=[cosnθsinnθ−sinnθcosnθ]nεN01:51View SolutionIf n is an integer then show that
(1+cosθ+isinθ)n+(1+cosθ−isinθ)n=2n+1cosn(θ/2)cos(nθ2).07:49View SolutionIf A=[cosθsinθ−sinθcosθ] then show that for all the positive integers n, An=[cosnθsinnθ−sinnθcosnθ].
07:35View Solutionसिद्ध कीजिए कि
[cosθ−sinθsinθcosθ]n=[cosnθ−sinnθsinnθcosnθ]03:51View Solution