यदि गोलक ax2+by2+cz2−2x+4y+2z−3=0 का (12,−1,−12) केंद्र है, तो b का मान क्या है ?
1
−1
2
−2
The correct Answer is:C
दिए हुए गोले का समीकरण निम्न हे
ax2+by2+cz2−2x+4y+2z−3=0
यह समीकरण एक गोले का समीकरण निरूपित करेगा, यदि
a=b=c
अतः गोले की समीकरण निम्न होगी
bx2+by2+bz2−2x+4y+2z−3=0
⇒x2+y2+z2−2bx+4by+2bz−3b=0
इस गोले का केंद्र (1b,−2b,−1b) है, परन्तु इस गोले का केंद्र
(12,−1,−12) दिया है |
∴ 1b=12⇒b=2
Related Playlists
- BOOK - NDA PATHFINDERCHAPTER - त्रिविमीय ज्यामिति EXERCISE - अभ्यास प्रश्नावली39videos
त्रिविमीय ज्यामिति
- BOOK - NDA PATHFINDERCHAPTER - त्रिविमीय ज्यामिति EXERCISE - विगत वर्षो के प्रश्न51videos
त्रिविमीय ज्यामिति
- BOOK - NDA PATHFINDERCHAPTER - त्रिभुजों के गुण EXERCISE - अभ्यास प्रश्नावली विगत वर्षों के प्रश्न12videos
त्रिभुजों के गुण
- BOOK - NDA PATHFINDERCHAPTER - द्विगुण संख्याएँ EXERCISE - अभ्यास प्रश्नावाली विगत वर्षों के प्रश्न14videos
द्विगुण संख्याएँ
Similar Questions
यदि एक रेखा अक्षों से बराबर कोण बनाएं, तो इसके दिक् अनुपात होंगे
05:04View Solutionयदि कोई रखा अक्षो से α,β तथा γ कोण बनाती है, तो 1+cos2α+cos2β+cos2γ का मान क्या है ?
01:33View Solutionयदि किसी ΔABC में , कोण A,B,C समान्तर श्रेढ़ी में हों ,तो निम्नलिखित में से कौन -सा एक सही है?
04:39View Solutionदशमलव पद्धति में संख्या 292 को द्वि - आधारी पद्धति में किसके द्वारा अभिव्यक्त किया जाता है ?
05:13View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
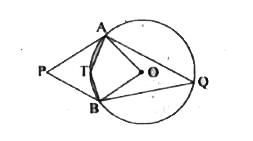 01:36View Solution
01:36View Solutionयदि ∣∣∣4121∣∣∣2=∣∣∣321x∣∣∣−∣∣∣x−3−21∣∣∣हो तो x का मान है-
02:11View Solutionमाना y=y(x), अवकल समीकरण (x2+1)2dydx+2x(x2+1)y=1 का हल है, जबकि y(0) = 0 है। यदि √ay(1)=π32 है तो 'α' का मान है
03:19View Solutionयदि (X0,Y0) समीकरणों (2x)log2=(3y)log3,3logx=2logy का हल है तो X0 का मान है
01:50View SolutionIf a+a2+a3−1=0, then what is the value of a3+(1/a)?
यदि a+a2+a3−1=0, है, तो a3+(1/a) का मान क्या है?02:06View SolutionIf (1//2^1)+(1//2^2)+(1//2^3).....+(1//2^10)= 1//k , then what is the value of k? यदि (1//2^1)+(1//2^2)+(1//2^3).....+(1//2^10)= 1//k है, तो k का मान क्या है?
01:51View SolutionIf [x-(1//x)] = 2 , then what is the value of [x^6-(1//x^6)] ? यदि [x-(1//x)] = 2 है, तो [x^6-(1//x^6)] का मान क्या है?
01:40View SolutionIf a+1a+2=0, then the value of a37−1a100 is
यदि a+1a+2=0, तो a37−1a100 का मान है-02:28View SolutionIf x-5 sqrtx-1=0 , then x^2+1/x^2 is equal to : यदि x-5 sqrtx-1=0 है, तो x^2+1/x^2 का मान क्या होगा ?
01:44View SolutionIf sqrtx+ 1/sqrtx= 2sqrt 2 , then x^2+1/x^2 is equal to: यदि sqrtx+ 1/sqrtx= 2sqrt 2 है, तो x^2+1/x^2 का मान क्या होगा ?
01:11View SolutionIf sqrtx- 1/sqrtx= 3sqrt 2 , then x^2+1/x^2 is equal to: यदि sqrtx- 1/sqrtx= 3sqrt 2 है, तो x^2+1/x^2 का मान क्या होगा ?
01:03View SolutionIf a+1a=2, then a4−1a4 is equal to :
यदि a+1a=2 है, तो a4−1a4 का मान क्या होगा ?01:42View Solution


