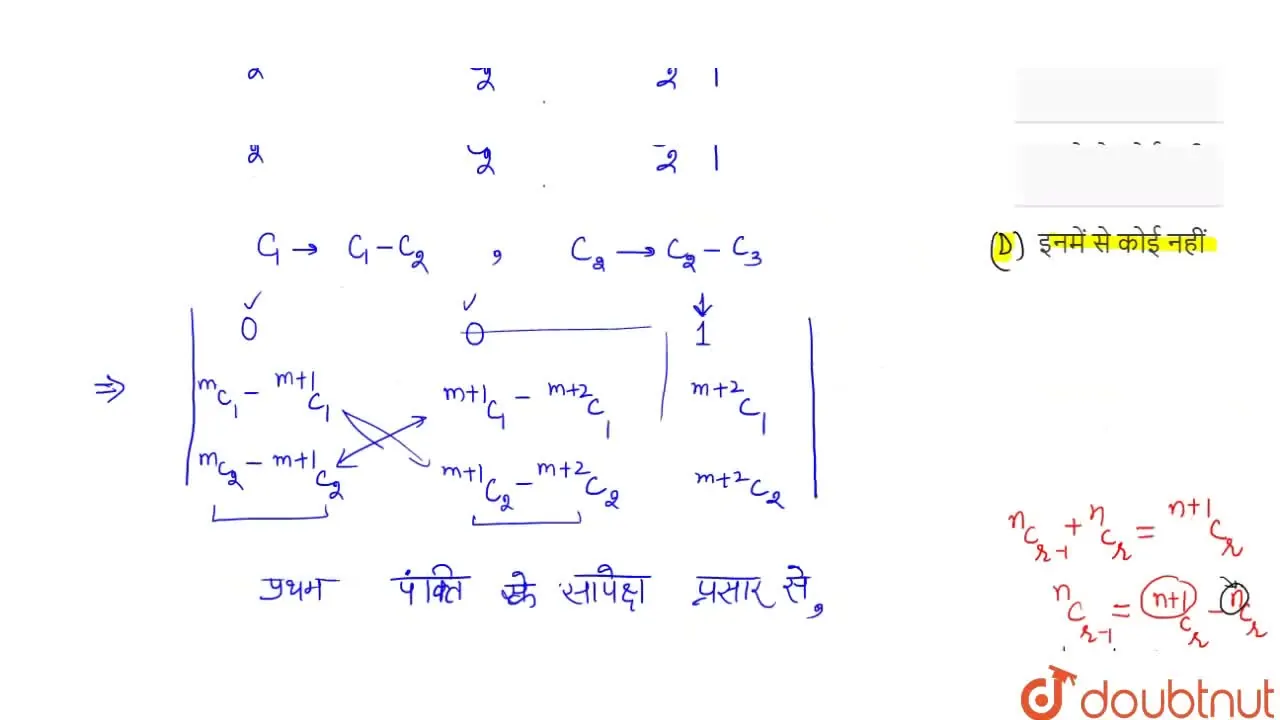
सारणिक का मान है
0
1
-1
इनमें से कोई नहीं
The correct Answer is:B
NA
Related Playlists
- BOOK - NOOTAN HINDICHAPTER - सारणिकEXERCISE - प्रश्नावली 4.18videos
सारणिक
- BOOK - NOOTAN HINDICHAPTER - सारणिकEXERCISE - प्रश्नावली 4.216videos
सारणिक
- BOOK - NOOTAN HINDICHAPTER - सारणिकEXERCISE - प्रश्नावली 4 F10videos
सारणिक
- BOOK - NOOTAN HINDICHAPTER - सम्बन्ध एवं फलन EXERCISE - विविध प्रश्नावली19videos
सम्बन्ध एवं फलन
Similar Questions
निम्नलिखित सारणिकों के मान ज्ञात कीजिएः
∣∣∣24−5−1∣∣∣07:35View Solutionबिना प्रसरण किए और सारणिकों के गुणधर्मों के प्रयोग करके निम्नलिखित प्रश्न को सिद्ध कीजिए-
∣∣ ∣ ∣∣xax+ayby+bzcz+c∣∣ ∣ ∣∣=003:22View Solutionसारणिक ∣∣∣−cosθsinθ−sinθ−cosθ∣∣∣ का मान है
View Solutionमान लीजिए कि f:R→R,f(x)=10x+7 द्वारा परिभाषित फलन है । एक ऐसा फलन g:R→R ज्ञात कीजिए जिसके लिए gof=fog=IR हो ।
View SolutionProve that ^mCn1Cm−mC2n2Cm+mC3n3Cm≡(−1)m−1nm.
09:34View SolutionIf m∈N and m≥2 prove that: ∣∣111 mC1 m+1C1 m+2C1 mC2 m+1C2 m+2C2∣∣=1 .
04:31View SolutionIf (1+x)n=c0+C1x+C2x2+…..+Xnxn,m≥2
C0−C1+C2−……+(−1).m−1Cm−1=(−1)m−1.n−1Cm−1.03:09View Solution.nC0+.n+1C1+.n+2C2…….+.nCm is equal to :
08:21View SolutionEvaluate ∣∣ ∣∣mC1mC2mC3nC1nC2nC3pC1pC2pC3∣∣ ∣∣
08:29View SolutionThe value of the determinant |(1,1,1),(.^(m)C_(1),.^(m +1)C_(1),.^(m+2)C_(1)),(.^(m)C_(2),.^(m +1)C_(2),.^(m+2)C_(2))| is equal to
05:25View SolutionIf m,n,r are positive integers such that r lt m,n, then ""^(m)C_(r)+""^(m)C_(r-1)""^(n)C_(1)+""^(m)C_(r-2)""^(n)C_(2)+...+ ""^(m)C_(1)""^(n)C_(r-1)+""^(n)C_(r) equals
03:22View Solutionसिद्ध कीजिए कि :
∣∣ ∣ ∣∣111mC1m+1C1m+2C1mC2m+1C2m+2C2∣∣ ∣ ∣∣=1.05:35View Solution∣∣ ∣ ∣∣111mC1m+1C1m+2C1mC2m+1C1m+2C2∣∣ ∣ ∣∣ का मान है -
02:22View Solution^(n)Cm+n−1Cm+n−2Cm+............+mCm
05:53View SolutionIf for 1≤m≤n,f(m,n)=C0−C1+C2−....+(−1)m−1⋅Cm−1, then f(7,8) is
05:53View Solution