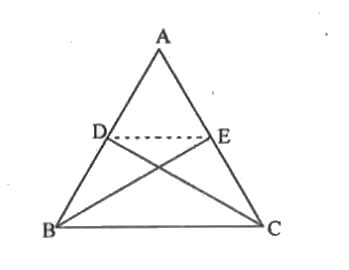
बिंदु D और E क्रमशः ΔABC की भुजाओं AB और AC पर इस प्रकार स्थित है की ar(DBC)=ar(EBC) है| दर्शाइए की DE∣∣BC है|
दिया है : ABC एक त्रिभुज है और D तथा E क्रमशः AB और AC पर स्थित है बिंदु इस तरह से की ar(DBC)=ar(EBC)
प्रमाण : चूँकि ΔDBC और ΔEBC एक ही आधार BC पर स्थित है|इसलिए उनकी ऊंचाइयों समान होगी|
अतः DE∣∣BC
ΔEBC एक ही आधार BC पर स्थित है तथा ये एक ही समांतर रेखाओं BC और DF के बिच स्थित है|
(##KCS_HIN_MAT_IX_C11_SLV_010_S01.png" width="80%">
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 11.124videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न7videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - वस्तुनिष्ठ प्रश्न9videos
समांतर चतुर्भुज
- BOOK - KC SINHACHAPTER - हीरोन का सूत्र EXERCISE - वस्तुनिष्ठ प्रश्न13videos
हीरोन का सूत्र
Similar Questions
रिक्त स्थान को भरें :
(i) सर्वांगसम आयतों के क्षेत्रफल ...........होते है|
(ii) किसी समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का .....होता है
(iii) समलम्ब का क्षेत्रफल उसके समांतर भुजाओं के बीच की दुरी तथा समांतर भुजाओं के योग के गुणनफल का ......होता है|
(iv) सर्वांगसम त्रिभुजों के क्षेत्रफल ........होते है|
(v) एक ही आधार तथा एक ही समांतर रेखाओं के मध्य बने त्रिभुज क्षेत्रफल में ...........होते है|03:56View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
03:50View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
02:20View Solutionयदि किसी ΔABC में BC=a,CA=b AB=c हो तो ΔABC की अर्धपरिमिति है
02:43View SolutionThe points D and E are respectively located on AB and AC on the sides of Delta ABC such that ar(DBC)=ar(EBC). Demonstrate that DE||BC.
02:21View Solutionबिंदु D और E क्रमश : ΔABC की भुजाओ AB और AC पर इस प्रकार स्थित है कि ar(DBC)=ar(EBC) है । दर्शाइए कि DE।।BC है ।
03:00View SolutionD and E are points on sides AB and AC respectively of Δ ABC such that ar (DBC) = ar EBC). Prove that DE∣∣BC.
 03:19View Solution
03:19View Solutionबिन्दु D और E क्रमश: ΔABC की भुजाओं AB और AC पर इस प्रकार स्थित है कि ar(DBC)=ar(EBC) है। दर्शाइए कि DE∣∣BC है।
03:09View SolutionD and E are points on sides AB and AC respectively of ti⟩ABC such that ar (DBC) = ar (EBC) . Prove that DE || BC
04:12View SolutionD and E are points on sides AB and AC respectively of ΔABC such that ar (DBC) = ar (EBC). Prove that DEIIBC.
05:03View SolutionPoints D and E, respectively triangle ABC The sides of AB are located on AB and AC in such a way that ar (DBC) = ar (EBC). Indicate that DE || BC.
04:17View SolutionIn triangle ABC , angle A is a right angle. The lengths of AC and BC 6 cm and 10 cm respectively. Point D is on AB such that BD = 4 cm. What is the length of CD? त्रिभुज ABC में, कोण A समकोण है | AC और BC की लंबाई क्रमशः 6 सेमी और 10 सेमी है | बिंदु D, AB पर इस प्रकार स्थित है कि BD = 4 सेमी है | CD की लंबाई ज्ञात करें |
06:40View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =3/4 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल में अनुपात ज्ञात करें |02:05View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =5/6 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =5/6 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल के बीच अनुपात ज्ञात करें |05:38View SolutionA circle touches the side BC of △ABC at D and AB and AC are produced to E and F, respectively. If AB = 10 cm, AC=8.6 cm and BC=6.4 cm, then BE = ?
एक वृत्त त्रिभुज ABC की भुजा BC को D पर स्पर्श करता है और AB तथा AC को क्रमशः E और F तक बढ़ाया जाता है | यदि AB = 10 सेमी, AC= 8.6 सेमी और BC=6.4 सेमी है, तो BE =?03:44View Solution
