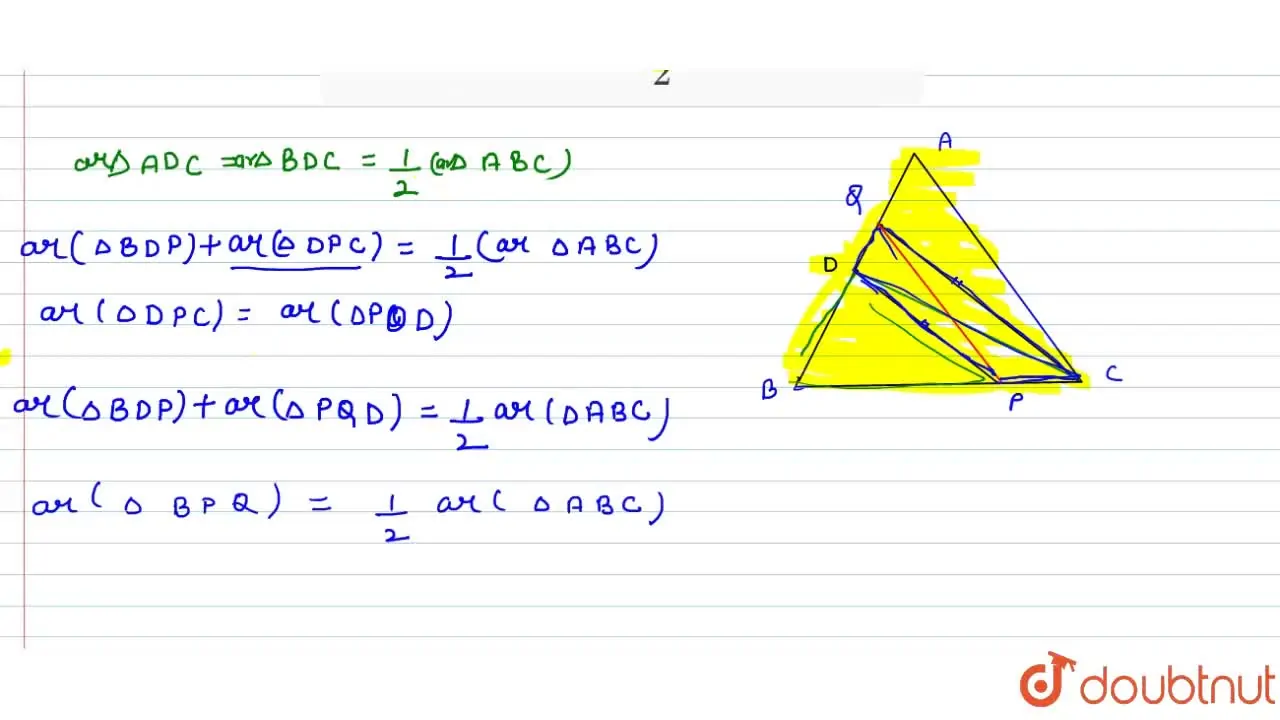
, में भुजा AB का मध्य-बिंदु D है तथा BC पर कोई बिंदु P है। यदि CQ ।। PD रेखा AB को Q पर मिलती है। सिद्ध कीजिए कि .
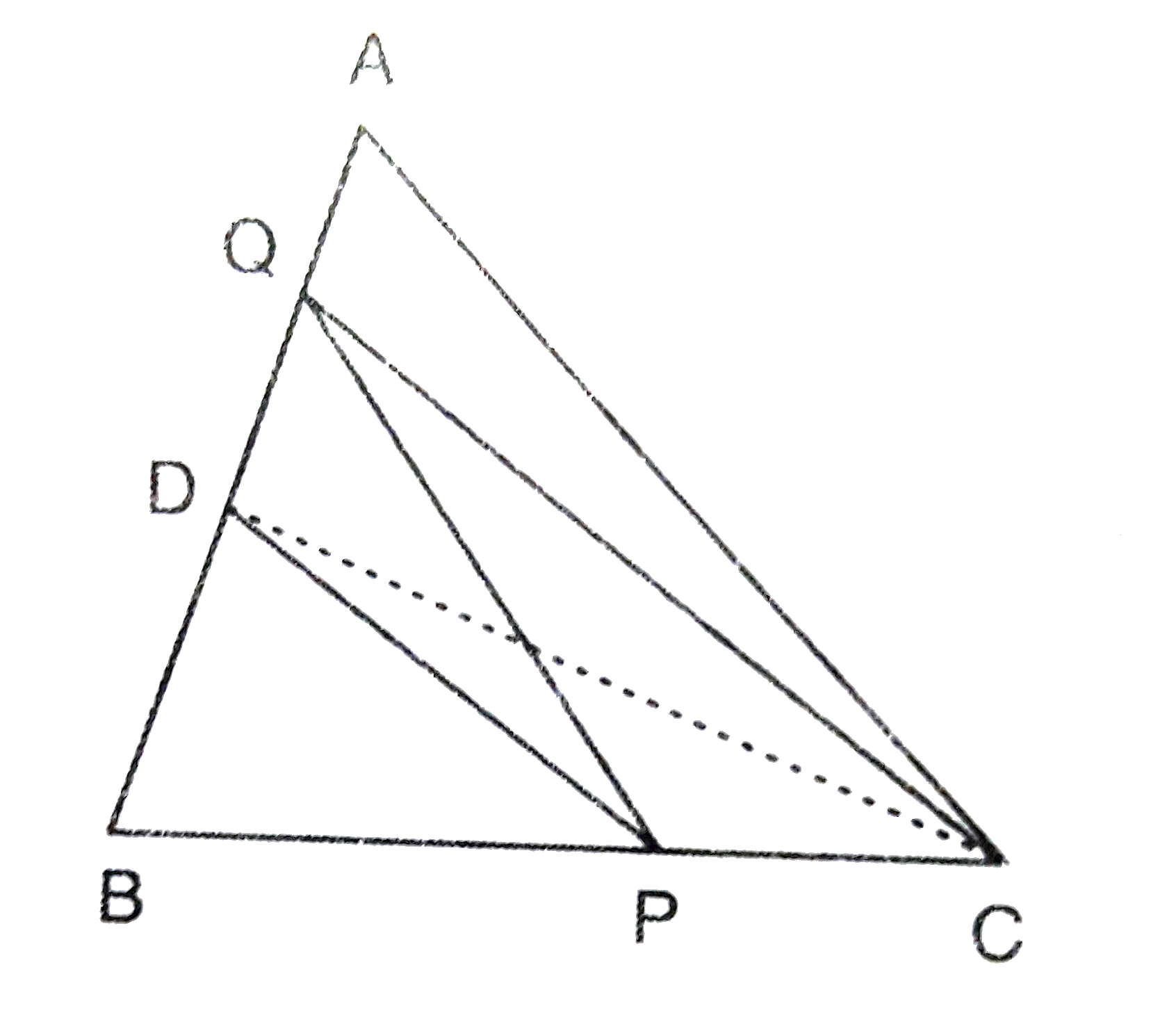
सिद्ध करना है:
रचना : CD को मिलाइये ।
उपपत्ति : चूँकि AB का मध्य-बिंदु D है। अतः , में CD एक माध्यिका है।
...(i)
चूँकि तथा एक ही आधार PD पर तथा एक ही समांतर रेखाओं PD तथा QC के बीच स्थित हैं।
...(ii)
अब, (i ) से
[ (ii ) से]
Related Playlists
- BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण1videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.16videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न8videos
संख्यिकीय आंकड़ों का आलेखीय निरूपण
- BOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न17videos
सर्वांगसम त्रिभुजें
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)
 03:28View Solution
03:28View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :
 View Solution
View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
03:05View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
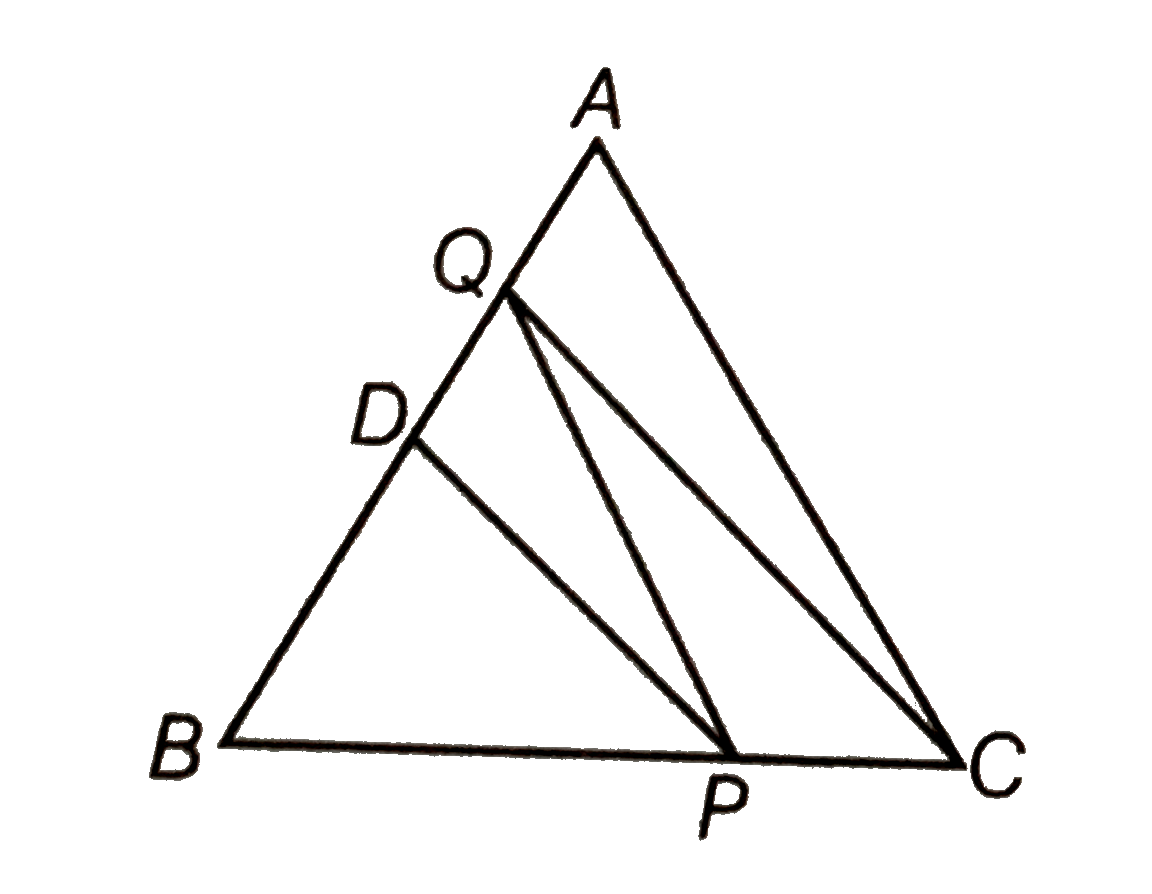
03:29View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
 03:29View Solution
03:29View SolutionΔABC में D भुजा AB का मध्य बिंदु है तथा P,BC पर कोई बिंदु है CQ∣∣PD,AB के बिंदु Q पर मिलती है। सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
03:38View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
04:39View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
05:05View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
05:40View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
03:34View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
04:26View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
05:07View SolutionAB एक ऊर्ध्वाधर खंभा है, जिनका A सिरा जमीन पर है | C, AB का मध्य-बिंदु है और P जमीन पर एक बिंदु है | BC, बिंदु P पर β कोण बनता है | यदि AP = nAB हो, तो tanβ का मान है |
02:50View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
 03:17View Solution
03:17View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
01:44View Solution