एक समान्तर चतुर्भुज ABCD के विकर्ण O पर प्रतिच्छेद करते है । यदि बिंदु O जाने वाली एक रेखा AB को X पर तथा CD को Y पर मिलती है, तो सिद्ध कीजिए कि
ar(□AXYD)=12ar(||gmABCD)
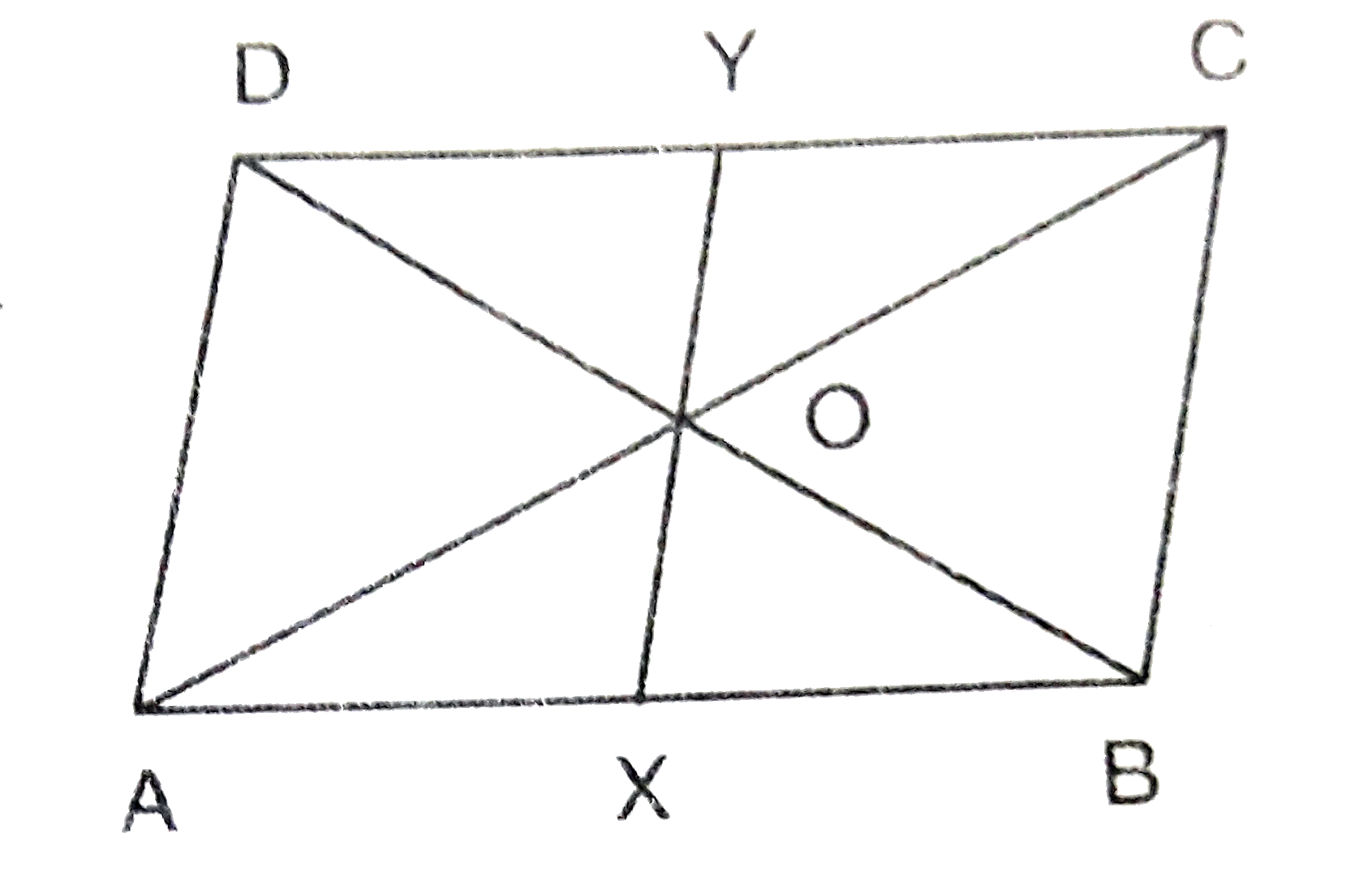
चूँकि समान्तर चतुर्भुज का विकर्ण इसे दो बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करता है। अतः ।।gm ABCD का विकर्ण AC इसे दो बराबर क्षेत्रफल वाले त्रिभुजों में बाँटता है।
∴ar(ΔACD)=12ar(||gmABCD) ...(i)
त्रिभुजों AOX तथा COY में
∠AOX=∠COY [ शीर्षभिमुख कोण बराबर होते है ]
AO=CO [∵||gm के विकर्ण परस्पर समद्विभाजित होते है∴ AC का मध्य-बिंदु O है]
तथा ∠OAX=∠OCY [∵ तथा तिर्यक रेखा AC इन्हें काटती है।∴∠CAB=∠ACD⇒∠OAX=∠OCY]
अतः कोण -भुजा-कोण सर्वांगसमता कसौटी से
ΔAOX≅ΔCOY
⇒ar(ΔAOX)=ar(ΔCOY) [सर्वांगसमता क्षेत्रफल अभिगृहीत द्वारा ]
⇒ar(ΔAOX)+ar(□AOYD)=ar(ΔCOY)+ar(□AOYD) [ दोनों पक्षों में ar(□AOYD) जोड़ने पर ]
⇒ar(□AXYD)=ar(ΔACD)
(i ) तथा (ii ) से
ar(□AXYD)=12ar(||gmABCD)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:व्याख्यात्मक उदाहरण
Explore 1 Video
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 15.1
Explore 6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण Book:RD SHARMAChapter:संख्यिकीय आंकड़ों का आलेखीय निरूपण Exercise:बहु विकल्पीय प्रश्न
Explore 8 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:बहु विकल्पीय प्रश्न
Explore 17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View Solutionबिन्दुओ (4,-1,2) और (-3,2,3) को मिलाने वाली रेखा एक समतल को बिंदु (-10,5,4) पर लंबवत मिलती है समतल का समीकरण ज्ञात कीजिये
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionबिंदु A(1,2) से होकर जाने वाली रेखा X-अक्ष के साथ 60∘ का कोण बनाती है तथा x+y=6 को बिंदु P पर काटती है तो AP की लम्बाई ज्ञात कीजिए
View Solutionसिद्ध कीजिए कि मूलबिंदु को एक उचित बिंदु(-1,-1) पर स्थान्तरित करके समीकरणों x+3y+4=0 और x−3y−2=0 को x+3y=0 तथा x−3y=0 के रूप में लिखा जा सकता है
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionबिन्दुओ(x',y')तथा (x'',y'') को मिलने वाली रेखा पर मूलबिंदु से डाले गये लम्ब कि लम्बाई ज्ञात कीजिए
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
View Solutionमाना बिंदु (h,k), (1,2) तथा (−3,4) एक रेखा L1 पर स्थित है। यदि बिन्दुओ (h,k) तथा (4,3) से होकर जाने वाली रेखा L2 रेखा L1 के लंबवत है, तो kh बराबर है
View Solutionयदि वृत्त x2+y2=1 की एक स्पर्श रेखा निर्देशांक अक्षो को भिन्न बिन्दुओ P और Q पर प्रतिच्छेद करती है, तो PQ के मध्य -बिंदु का बिन्दुपथ (locus) है
View Solution

