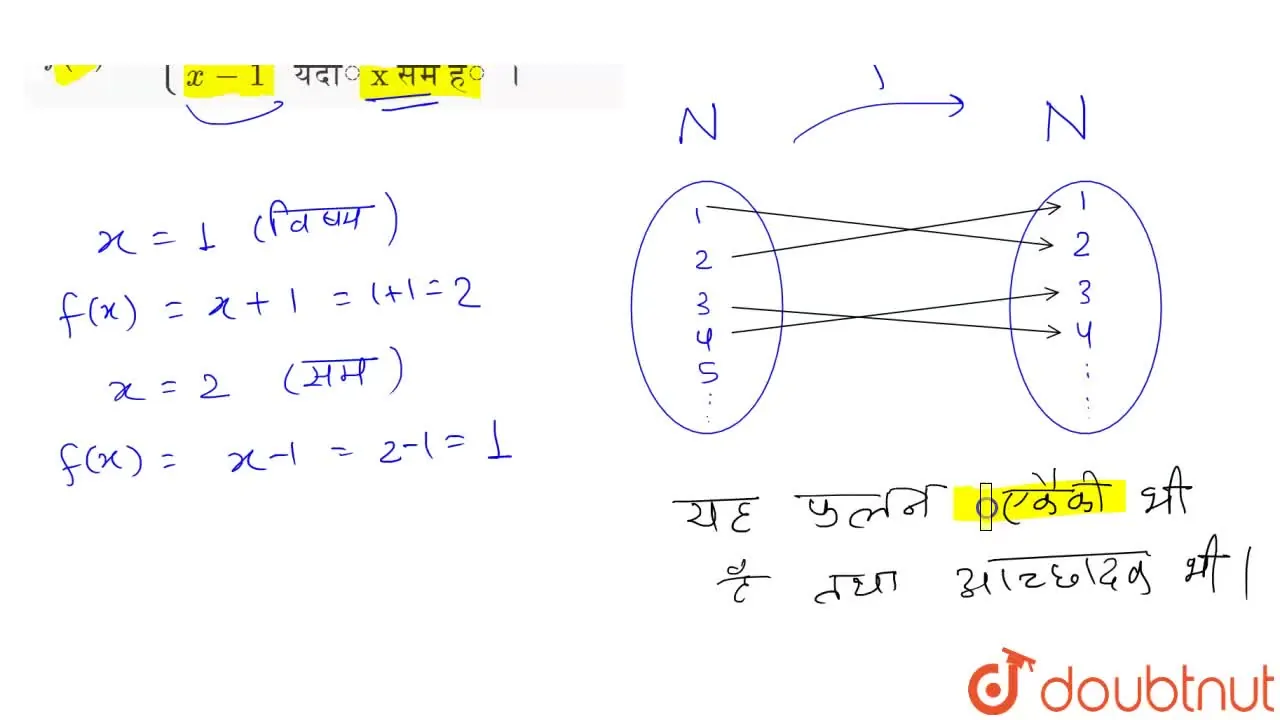
दिखाएँ कि f:N→N जो
f(x)={x+1, यदि x विषम हैx-1, यदि x सम है
से परिभाषित है, एक एकैकी आच्छादक है।
साबित करना है कि f एकैकी है:
माना कि m, n∈ प्रान्त N
Case I. यदि m और n दोनों सम हैं, तो
f(m)=f(n)⇒m−1=n−1
⇒m=n
Case II. यदि m और n दोनों विषम है, तो
f(m)=f(n)⇒m+1=n+1
⇒m=n
Case III. यदि m विषम तथा n सम है, तो
f(m)=f(n)⇒m+1=n+1
∴f(m)≠f(n) [∵m+1 सम है तथा n-1 विषम है]
Case IV. यदि m सम तथा n विषम है, तो
f(m)=f(n)⇒m−1=n+1
लेकिन m-1 विषम है तथा n+1 सम है।
∴m−1≠n+1
∴f(m)≠f(n)
इस प्रकार सभी स्थितियों मे
f(m)=f(n)⇒m=n
अतः f एकैकी है।
साबित करना है कि f आच्छादक है:
माना कि k सहप्रान्त N का एक स्वेच्छ अवयव है।
Case I. यदि k विषम है, तो (k+1) सम होगा ।
अब f(k+1)=(k+1)−1 [ f की परिभाषा से ]
= k
इस प्रकार k+1∈ प्रान्त का N, k प्रतिबिम्ब है।
Case II. यदि k सम , तो (k-1) विषम होगा
f(k−1)=(k−1)+1 [f की परिभाषा से ]
इस प्रकार k∈ सहप्रान्त N,k−1 का प्रतिबिम्ब है।
अतः सहप्रान्त N का प्रत्येक अवयव, प्रान्त के किसी-न-किसी अवयव का प्रतिबिम्ब है।
अतः f आच्छादक है।
इस प्रकार f एकैकी आच्छादक है।
Related Playlists
- BOOK - KC SINHACHAPTER - फलन EXERCISE - अभ्यास 2.129videos
फलन
- BOOK - KC SINHACHAPTER - फलन EXERCISE - अभ्यास 2.212videos
फलन
- BOOK - KC SINHACHAPTER - प्रायिकता का गुणन प्रमेय EXERCISE - 32.224videos
प्रायिकता का गुणन प्रमेय
- BOOK - KC SINHACHAPTER - बरनौली परीक्षण और द्विपद बंटन EXERCISE - OBJECTIVE QUESTIONS10videos
बरनौली परीक्षण और द्विपद बंटन
Similar Questions
माना कि A = {1, 2, 3}, B = {4, 5, 6, 7} तथा माना कि f = {(1, 4), (2, 5), (3, 6)} A से B में एक फलन है। दिखाएँ कि f एकैकी है।
View Solutionमाना कि f = {(1, 2), (3, 5), (4, 1)} तथा g = {(2, 3), (5, 1), (1, 3)} द्वारा प्रदत्त है। fog तथा gof ज्ञात करें।
08:21View Solutionएक न्यायय सिक्का और एक अभिनत पाए को उछाला गया । मान ले A घटना 'सिक्के पर चित प्रकट होता है और B घटना 'पास पर संख्या 3 प्रकट होती है' को निरूपित करते है। परीक्षण कीजिए की घटनाएँ A और B स्वतंत्र है या नहीं ?
View SolutionIn a box containing 100 bulbs , 10 are defective. What is the probability that out of a sample of 5 bulbs, none is defective ?
View Solutionमाना कि f:Z→Z इस प्रकार परिभाषित है:
f(x)={x, यदि x सम हैx+1, यदि x विषम है
क्या g:Z→Z का अस्तित्व है ताकिView Solutionनिम्नलिखित फलन के प्रकार की जाँच करें f:R→R जो इस प्रकार परिभाषित है
(i) f(x)=x3 (ii) f(x)={1, यदि x परिमेय है-1, यदि x अपरिमेय है05:12View Solutionदर्शाई की फलन f:N→N जो की f(x)={x+1,यदि x विषम हैx-1,यदि x सम है
से परिभाषित है एकेकी व् आच्छादक है03:05View Solutionदिखाइए की f:N−N जबकि
f(x)={n+12,यदि n विषम है|n2,यदि n सम है ।
एक बहु-एक आच्छादक फलां है |02:58View Solutionमाना f:Z→Z जबकि
f(n)={(n−1)यदिन विषम है(n+1)यदिन सम है
दर्शाइए की f व्यूत्क्रणीय है व् f−1 ज्ञात कीजिय03:05View Solutionयदि f:N∪{0}→N∪{0} निम्न प्रकार परिभाषित हैं -
f(x)={n+1, यदि n सम है n−1,यदि n विषम है,
सिद्ध कीजिए f व्युत्क्रमणीय फलन है ।04:51View Solutionसिद्ध कीजिए कि नीचे परिभाषित फलन f:N→N, एकैकी तथा आच्छादक दोनों ही है :
f(x)={x+1,यदि x विषम हैx−1,यदि x सम है02:47View Solutionमान लीजिए कि f:[0,1]→[0,1],f(x)={x,यदि x परिमेय है1−x,यदि x अपरिमेय है द्वारा परिभाषित है , तो (fof)x:
View Solutionसिद्ध कीजिए कि नीचे परिभाषित फलन f:N→N, एकैकी तथा आच्छादक दोनों ही है-
f(x)={x+1 यदि x विषम है x−1यदि x सम है ।03:18View Solutionयदि f(x)=xयदिx परिमेय है 0यदिx अपरिमेय है तथा g(x)=0यदिx परिमेय हैx यदिx अपरिमेय है तबf−g है
04:52View Solutionयदि cot x-tan x = 2 है, तो व्यापक हल है (यहाँ, n एक पूर्णांक है)
02:17View Solution