The wave function unnormalized for a particle moving in a one dimensional potential well Vx is given by ψx = exp−ax2/2. If the potential is to have minimum value at x = 0 determine a the eigen value b the potential Vx.
Schrodinger’s equation in one dimension is
Related Solutions
A particle of mass m is moving in a potential well, for which the potential energy is given by where and a are positive constants. Then (for the small value of x)
View SolutionA particle of mass m is moving in a potential well, for which the potential energy is given by where and a are positive constants. Then (for the small value of x)
View SolutionA particle moves along x-axis whose potential energy versus x-coordinate graph is shown in the given figure. At x = 0, the particle is released form rest. Two potential wells A and B are shown in the figure. Then,
View SolutionA particle located in one dimensional potential field has potential energy function, where a and b are positive constants. The position of equilibrium corresponds to x equal to
View SolutionA particle located in a one-dimensional potential field has its potential energy function as , where a and b are positive constants. The position of equilibrium x corresponds to
View SolutionA particle located in one dimensional potential field has potential energy function U(x)=(a)/(x^(2))-(b)/(x^(3)) , where a and b are positive constants. The position of equilibrium corresponds to x equal to
View SolutionA particle located in one dimensional potential field has potential energy function U(x)=(a)/(x^(2))-(b)/(x^(3)) , where a and b are positive constants. The position of equilibrium corresponds to x equal to
View SolutionA particle located in a one-dimensional potential field has its potential energy function as U(x)(a)/(x^4)-(b)/(x^2) , where a and b are positive constants. The position of equilibrium x corresponds to
View SolutionAn electron is in a one-dimensional trap with zero potential energy in the interior and infinite potential energy at the walls. A graph of its wave function y(x) versus x is shown in the following figure. The value of quantum number n is
View Solutionआयनन विभव का न्यूनतम मान है :
View SolutionA particle moves in a one dimensional field. Its total mechanical energy is E. If the potential energy of the particle is U(x), then -
View SolutionA particle free to move along the X- axis has potential energy given by U(X)=k[1-exp(-X^(2))] of appropriate dimensions. Then-
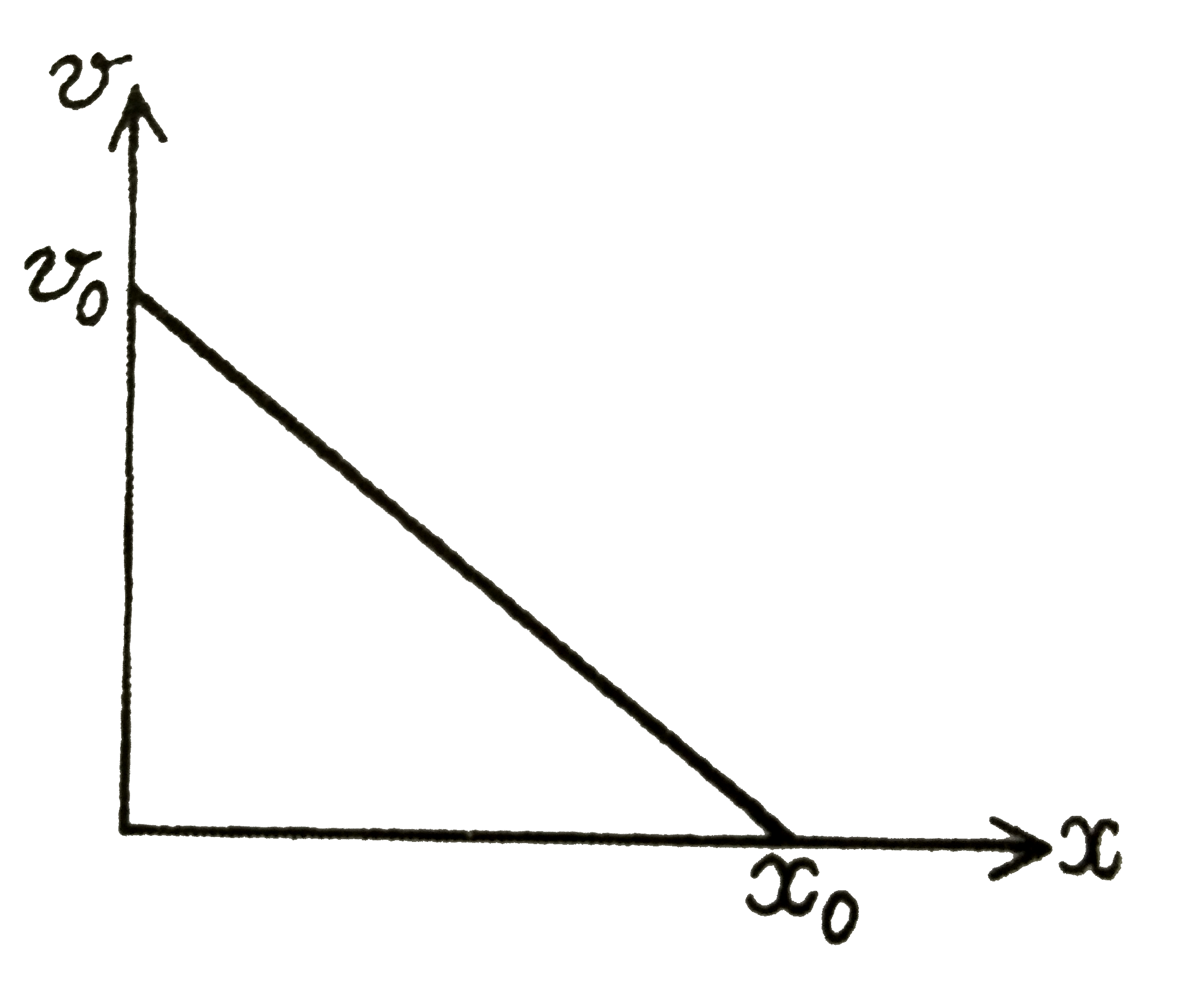
View Solutionएक सीधी रेखा के अनुदिश गतिमान कण का वेग -दूरी (v-x) ग्राफ संलग्न चित्र में दिखाया गया है । निम्नांकित में से कौन-सा त्वरण दूरी (a-x) ग्राफ दिये गये वेग-दूरी ग्राफ दिये गये वेग-दूरी (v-x) ग्राफ के संगत है ?
View SolutionA particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form U (x) = (a)/(x^(2)) - (b)/(x) where a and b are positive constants. The position of equilibrium is:
View SolutionA particle of mass m moves in a one dimensional potential energy , where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=-ax^2+bx^4 , where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=-ax^2+bx^4 , where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionThe velocity-distance (vx) graph of a particle moving along a straight line is shown in the attached figure, which of the following acceleration-distance (ax) graphs correspond to the given velocity-distance (vx) graphs.
View SolutionFor what value of the potential of is equal to the potential of ?
View Solution