The following figure shows the graph of a continuous function y = fx on the interval [1 3]. The points A B C have coordinates 1 1 3 2 2 3 respectively and the lines L1 and L2 are parallel with L1 being tangent to the curve at C. If the area under the graph of y = fx from x = 1 to x = 3 is 4 square units then the area of the shaded region is-A 2 B 3 C 4 D 5
The correct Answer is:Option
Correct Option :- A 2 Explanation :-
Related Solutions
The following figure shows the graph of a continuous function y = f(x) on the interval [1, 3]. The points A, B, C have coordinates (1,1), (3,2),(2,3), respectively , and the lines L_(1) and L_(2) are parrallel, with L_(1) being tangent to the curve at C. If the area under the graph of y = f(x) from x = 1 to x = 3 is 4 square units, then the area of the shaded region is
View SolutionThe folloiwng figure shows the graph of a continuous function y = f(x) on the interval [1, 3]. The points A, B, C have coordinates (1,1), (3,2),(2,3), respectively , and the lines are parrallel, with being tangent to the curve at C. If the area under the graph of y = f(x) from x = 1 to x = 3 is 4 square units, then the area of the shaded region is

View SolutionThe following shows the graph of a continuous function on the interval . The points A, B, C have coordinates respectively, and the lines and are parallel, with being tangent to the curve at C. If the area under the graph of from to is 4 square units, then the area of the shaded region is -
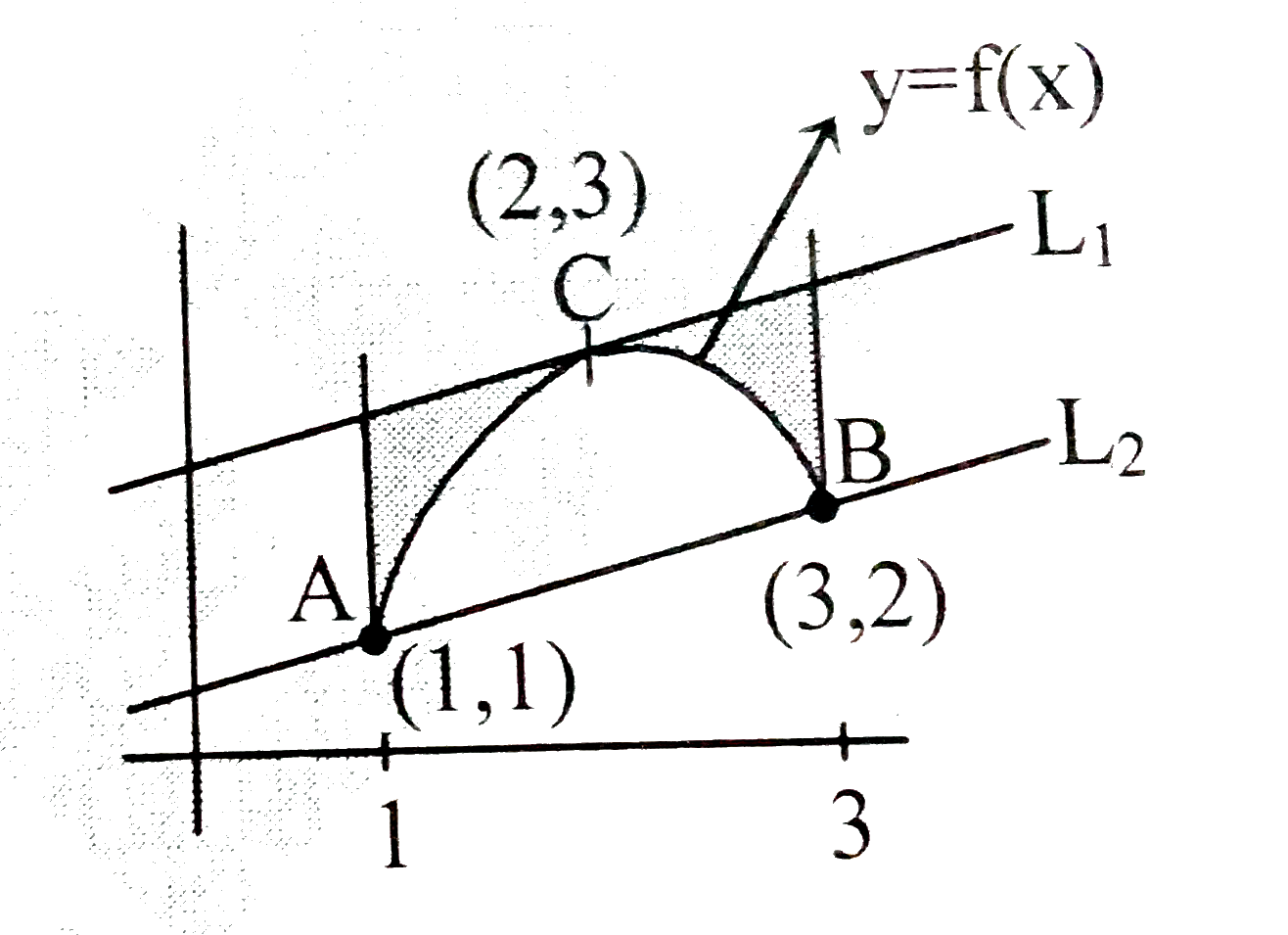
View SolutionThe following diagram shows the continuous function y = f (x) at the [1,3] interval. The coordinates of A, B, C are (1, 1), (3, 2) and (2, 3) respectively: L_1 And L_2 The lines are parallel, L_1 Is the tangent line that touches the curve at C. If y = f (x) the area under the graph is 4 square units from x = 1 to x = 3, then what is the area of the covered area?
View SolutionLet be two lines such that
The point of intersection of is
View SolutionConsider the line
The shortest distance between and is
View Solutionif line 2x+7y-1=0 intersect the lines L1:3x+4y+1=0 and L2:6x+8y-3=0 in A and B respectively,then equation of line parallal to L1 and L2 and passes through a point P such that AP:PB=2:1 (internally) is (P is on the line 2x + 7y-1=0)
View SolutionConsider two points A and B on L1 and a line L2 as shown in figure. Find the foot of the perpendicular drawn from (2,3,4) on L1 to the line L2.
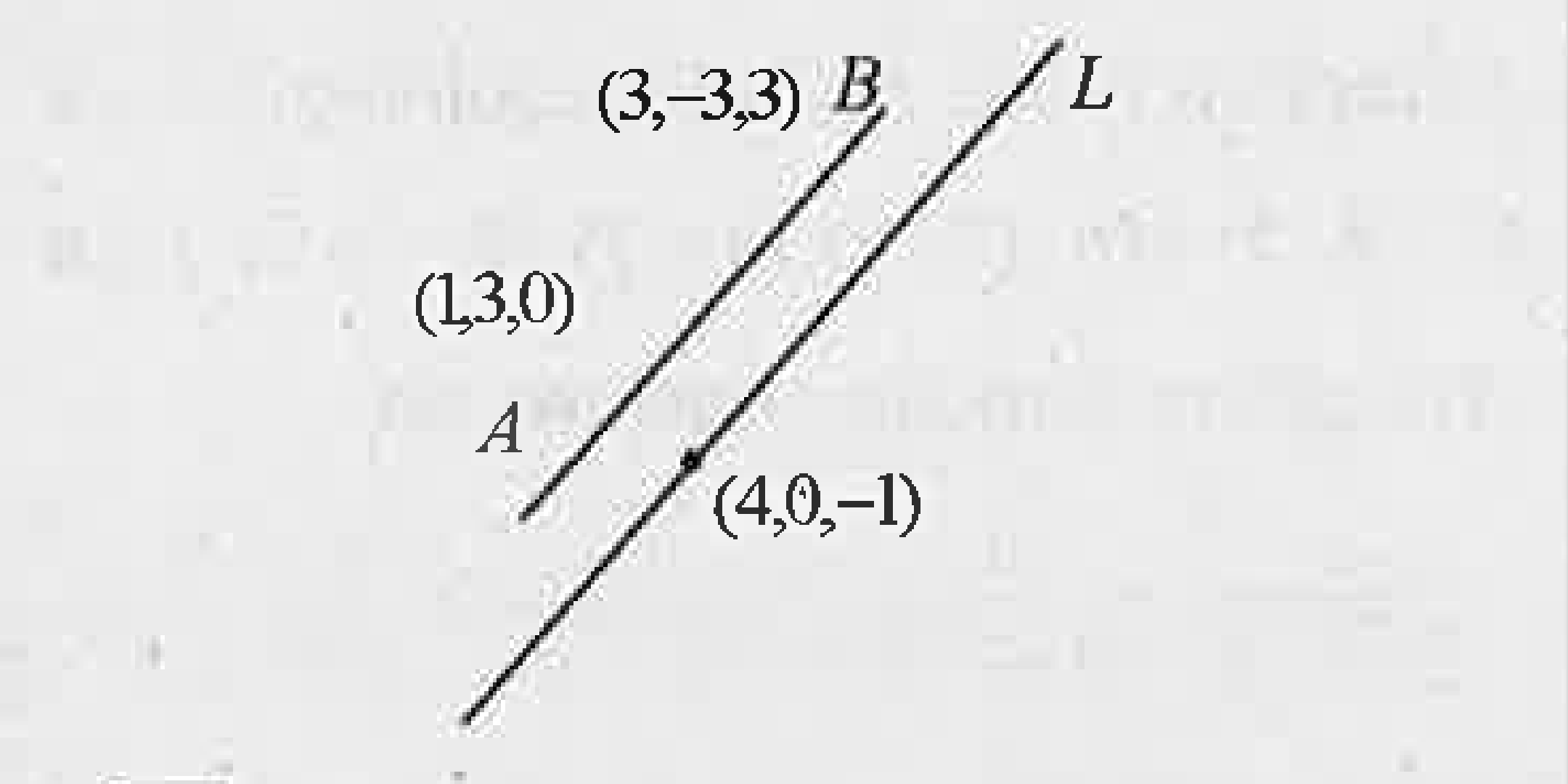
View SolutionFind a point on the curve , when the tangent is parallel to the chord joining (1,1), (3,27).
View SolutionFind the value of so that the lines l1: (1-x)/3 = (7y-14)/(2lambda) =(z-3)/2 and l2: (7-7x)/(3lambda) = (y-5)/1 = (6-z)/5 are at right angle. Also find the equation of a line passing through the point (3,2,-4) and parallel to l1.
View SolutionThe maximum area of triangle formed by a tangent line to the curve =1 and the coordinates axes is
View SolutionFunction y=2x-4x^(3) A part of the graph of K is shown in the given figure. The line y = c is such that the areas of regions I, II are equal. If the x-coordinates of the points A, B are a, b respectively, then the value of a + b will be
View SolutionDetermine the area of the triangle formed by the tangent to the graph of the function y=3- drawn at the point (1,2) and the coordinate axes.
View SolutionThe point at which the tangent to the curve is parallel to the line y = 3 x + 9 is
View SolutionFind a point on the graph of the curve , where the tangent is parallel to the chord joining (3,0) and (4,1)
View SolutionGiven the graphs of the two functions, y= f(x) & y =g(x). In theadjacent figure from point A on the graph of the function y fx)corresponding to the given value of the independent variable (say x),a straight line is drawn parallel to the X-axis to intersect the bisectorof the first and the third quadrants at point B. From the point B astraight line parallel to the Y-axis is drawn to intersect the graph ofthe function y= g(x) at C. Again a straight line is drawn from the point C parallel to the X-axis, to intersect the line NN' at D. If thestraight line NN' is parallel to Y-axis, then the co-ordinates of the point D are
View SolutionThe distance between the graphs of the equations is:
(a) 2
(b) 4
(c) 3
(d) 1
View SolutionIn the figure given below there are two convex lenses L1 and L2 having focal lengths F1 and F2 respectively. The distance between L1 and L2 will be
View SolutionFind the coordinates of the point on the curve where tangent is parallel to the line .
View SolutionFind the coordinates of the point on the curve where tangent is parallel to the line .
View Solution