Prove that ∫xm - 1 + xn - 1/1 + xm + ndx for x ∈ [0 1] = βm n.
From the relation In the second integral on R.H.S. of 1Substitute x = 1/t so that dx = – dt/t2 when x = 1 t = 1 andwhen x = ∞ t = 0
Related Solutions
m (1)/(xn) ((1)/(sin (pi x))-((-1)^(n))/(pi (xn))) = ((-1)^(n) pi )/(k), (n in Z)
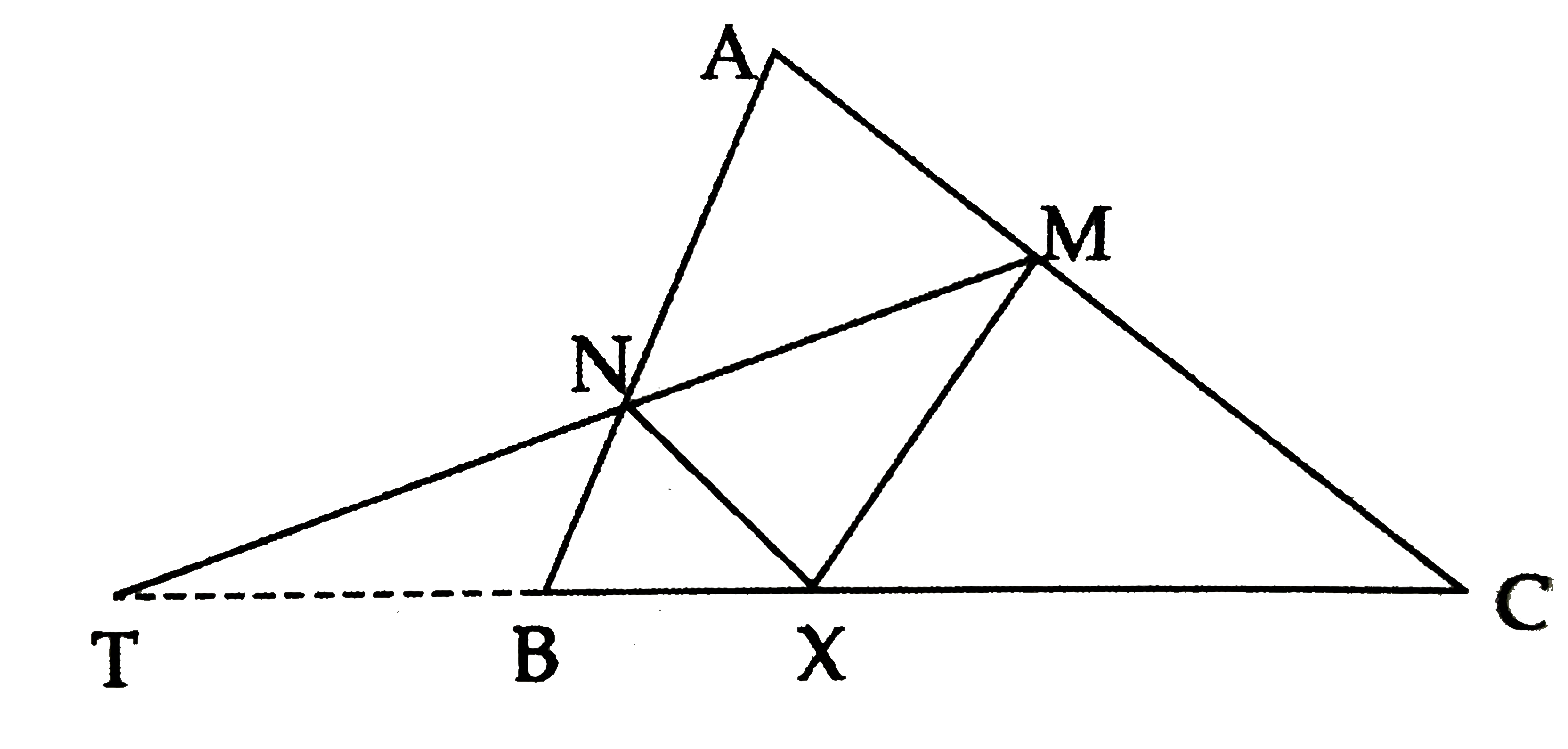
View SolutionLet X be any point on side BC of XM and XN are drawn parallel to BA and CA. MN meets in T. Prove that

View SolutionSolve the equation
View SolutionA freely falling body traveled xm in second distance travelled in second is
View SolutionA freely falling body traveled xm in second distance travelled in second is
View SolutionA freely falling body traveled xm in second distance travelled in second is
View SolutionA freely falling body traveled xm in second distance travelled in second is
View SolutionA freely falling body traveled xm in n^(th) second distance travelled in n-1^(th) second is
View SolutionLet X be any point on side BC of seg XM || side AB and seg XN ||side CA . M - N- T , T - B - X . Prove that :
View SolutionIf n_(j_(r))=((1-xn)(1-x(n-1))(1-x^(n-2)).......(1-x^(n-r+1)))/((1-x)(1-x^2)(1-x^3)........(1-x^r)), prove that n_(j_(n-r) = n_(j_(r.))
View SolutionTrue or False: , where n is any integer.
View SolutionProve that
View SolutionIf m!=n and (m+n)^(-1)(m^(-1)+n^(-1))=m^xn^y then show that x+y+2=0
View SolutionIf det[[a,a,xm,m,mb,x,b]]=0 then x=
View SolutionIf det[[a,a,xm,m,mb,x,b]]=0 then x=
View SolutionIf det[[a,a,xm,m,mb,x,b]]=0 then x=
View SolutionIf det[[a,a,xm,m,mb,x,b]]=0 then x=
View Solution
View SolutionIf and , then (A) (B) (C) (D) none of these
View SolutionIf and , then (A) (B) (C) (D) none of these
View Solution