Let A be one point of intersection of two intersecting circles with centres O and Q. The tangents at A to the two circles meet the circles again at B and C respectively. Let the point P be located so that AOPQ is a parallelogram. Prove that P is the circumcentre of the triangle ABC.
Answer is ......Thus P is the point of intersection of perpendicular bisectors PQ and PO of sides AC and AB respectively.Hence P is the circumcentre of ΔABC.
Related Solutions
Let be one point of intersection of two intersecting circles with centres . The tangents at to the two circls meet the circles again at , respectively. Let the point be located so that is a parallelogram. Prove that is the circumcentre of the triangle .
View SolutionLet A be one point of intersection of two intersecting circles with centres O and Qd . The tangents at A to the two circles meet the circles again at B and C respectively. Let the point P be located so that AOPQ is a parallelogram. Prove that P is the circumcentre of the triangle ABC.
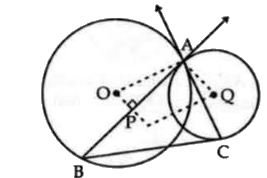
View Solutionमान लीजिए कि केंद्र O तथा Q वाले दो व्रतों का एक प्रतिच्छेद बिंदु A है । दोनों व्रतों की बिंदु A पर स्पर्श रेखाएँ व्रतों को क्रमशः फिर से B तथा C पर मिलती हैं । मान लीजिए बिंदु P इस प्रकार खोजा गया है कि AOPQ एक समान्तर चतुर्भुज है । सिद्ध कीजिए कि P त्रिभुज ABC का परिकेन्द्र है ।
View SolutionTwo circles intersects in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that the A,Q,B and T lie on a circle.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and
the other circle at B and D. Prove the AC|| BD
View Solutionகொடுக்கப்பட்ட படத்தில் O மையமாக உடைய வட்டத்தின் ஆரம் 5 செ .மீ ஆகும் .T ஆனது OT =13 செ .மீ என அமைந்த ஒரு புள்ளி மற்றும் OT ஆனது வட்டத்தை E ல் வெட்டுகிறது,வட்டத்தின் E என்ற புள்ளியின் வழியாக செல்லும் ஒரு தொடுகோடு AB எனில் ,AB -யின் நீளம் காண்க ?
View SolutionLet P and Q be two points on a circle with centre O. If two tan gents of the circle through P and O meet at A with , then is
View SolutionLet P and Q be two points on the circle |w|=r represented by and respectively, then the complex number representing the point of intersection of the tangents of P and Q is :
View SolutionLet P and Q be two points on the circle |w|=r represented by and respectively, then the complex number representing the point of intersection of the tangents of P and Q is :
View SolutionLet P and Q be two points on the circle |w|=r represented by and respectively, then the complex number representing the point of intersection of the tangents of P and Q is :
View SolutionIn two circles , one circle passes through the centre O of the other circle and they intersect each other at the points A and B . A straight line passing through A intersect the circle passing through O at the point P and the circle with centre at O at the point R . BY joining P , B and R , B prove that PR= PB.
View SolutionTwo circle with centre O and P intersect each other in point C and D. Chord AB of the circle with centre O touches the circle with circle with centre P in Point E. Prove that
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
View SolutionDraw two central circles A and B which intersect each other at the point O. Draw a straight line with the point O which intersects the two circles at points P and Q respectively. Prove that AP||BQ ।
View SolutionTwo circles with centres O and of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP are tangents to the two circles. Find the length of the common chord PQ.
View SolutionTwo circles with centres O and O' of radii 3cm and 4 cm, respectively intersect at two points P and Q, such that OP and O' P are tangents to the two circles. Find the length of the common chord PQ.
View SolutionSahana draws two circles that intersect at points P and Q. If PA and PB are the diameters of two circles, respectively, prove that the points A, Q and B are equidistant.
View SolutionTwo circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic.
View SolutionP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If them is-
View Solution