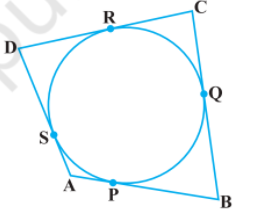
A quadrilateral ABCD is drawn to circumscribe a circle Figure given. Prove that AB + CD = AD + BC.
Since lengths of two tangents drawn from an external point of circle are equal Therefore AP = AS BP = BQ and DR = DSCR = CQ [Where P Q R and S are the points of contact]Adding all these we haveAP + BP + CR + RD = BQ + CQ + DS + AS⇒ AB + CD = BC + DAHence proved.
Related Solutions
Quadrilateral ABCD is drawn to circumscribe a circle. Prove that .
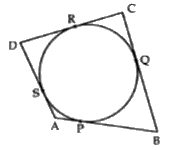
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle (see the given figure). Prove that AB+CD = AD+BC.
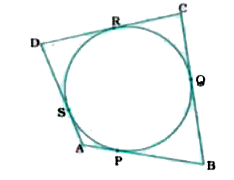
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that

View SolutionA quadrilateral ABCD is drawn to circumscribe a circle (see Figure).Prove that AB+CD=AD+BC.
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that

View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that
or
A circle touches all the four sides of a quadrilateral ABCD. Prove that
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC.
or
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB+CD=BC+DA.
View SolutionA quadrilateral ABCD is drawn to tu circumscribe a circle. Prove that .
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle(seeFig).Prove that
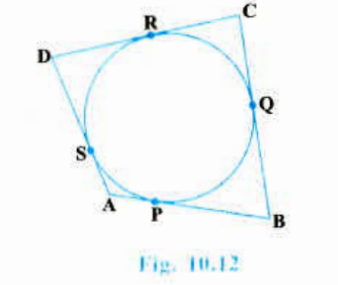
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle as shown. Prove that AB+CD=AD +BC.
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle as shown . Prove that
View Solutionएक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है सिद्ध कीजिए
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that
View SolutionQradrilateral ABCD circumscribes a circle. Prove that .
View Solutionएक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है (देखिए आकृति)। सिद्ध कीजिए : AB+CD=AD+BC

View SolutionA quadrilateral ABCD is drawn to circumscribe a circle(seeFig).Prove that

View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
View Solutionएक वृत्त के परिगत एक चतुर्भुज ABCD खिंचा गया हैं जैसा कि चित्र में दिखाया गया करें कि AB + CD = AD + BC
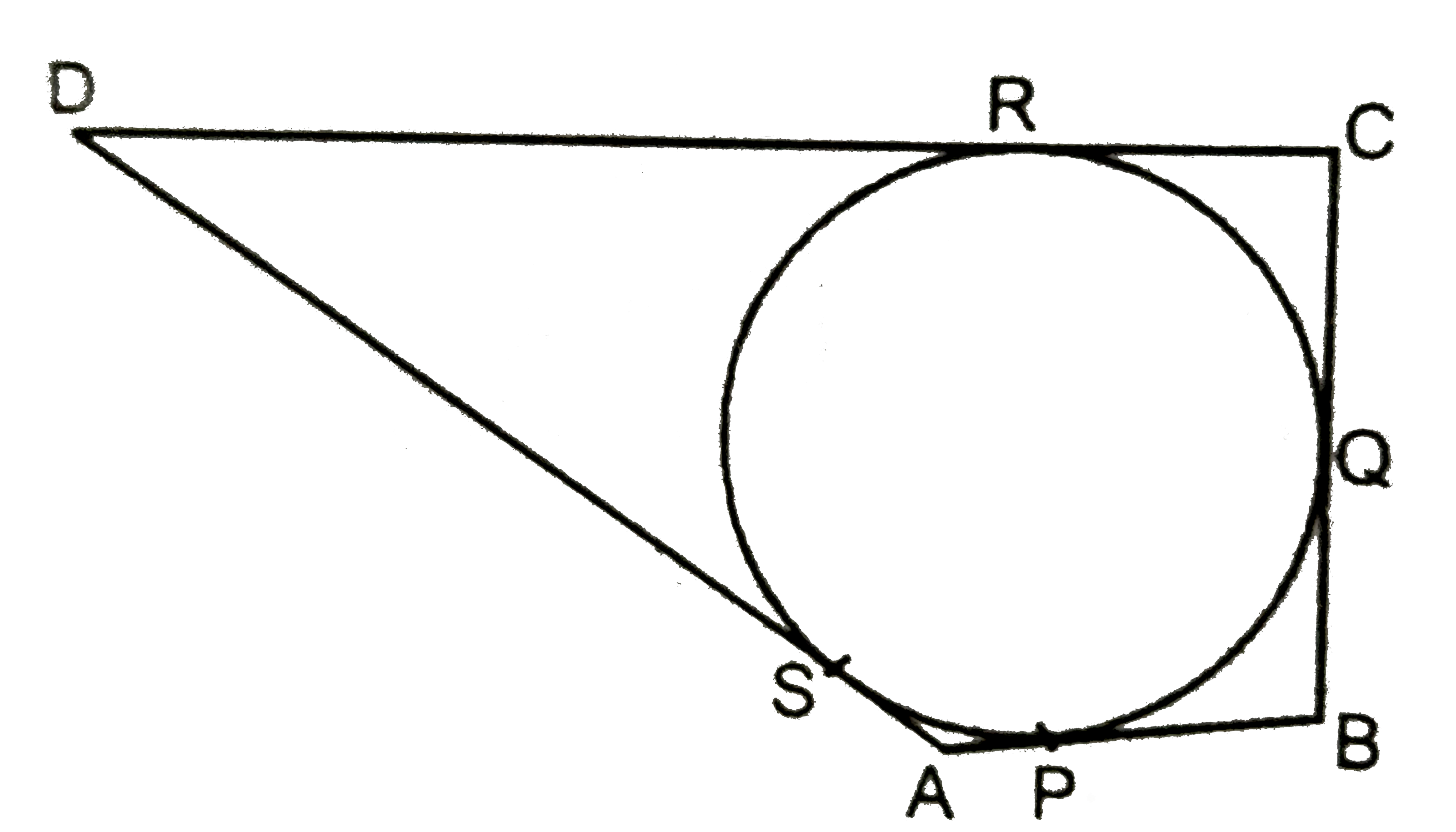
View Solution