A particle executing SHM has its acceleration represented by the equation f = – 4π2 y. Calculate its time period.
f = – 4π2 y = –ω2 y where ω2 = 4π2
Related Solutions
A particle executing SHM has an acceleration of with its displacement is 4 cm. Its time period, in seconds is……………
View SolutionA particle executing SHM has an acceleration of when its displacement is 2 cm. find the time period.
View SolutionEquation of SHM is y=3sin60pit . Calculate its amplitude, time period and acceleration at its position of maximum displacement.
View SolutionA particle executes SHM represented by the equation , y= 0.02sin(3.14t+ (pi)/(2)) meter. Find time period
View SolutionAcceleration-displacement graph of a particle executing SHM Is as shown in given figure. The time period of its oscillation is: (in sec)

View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
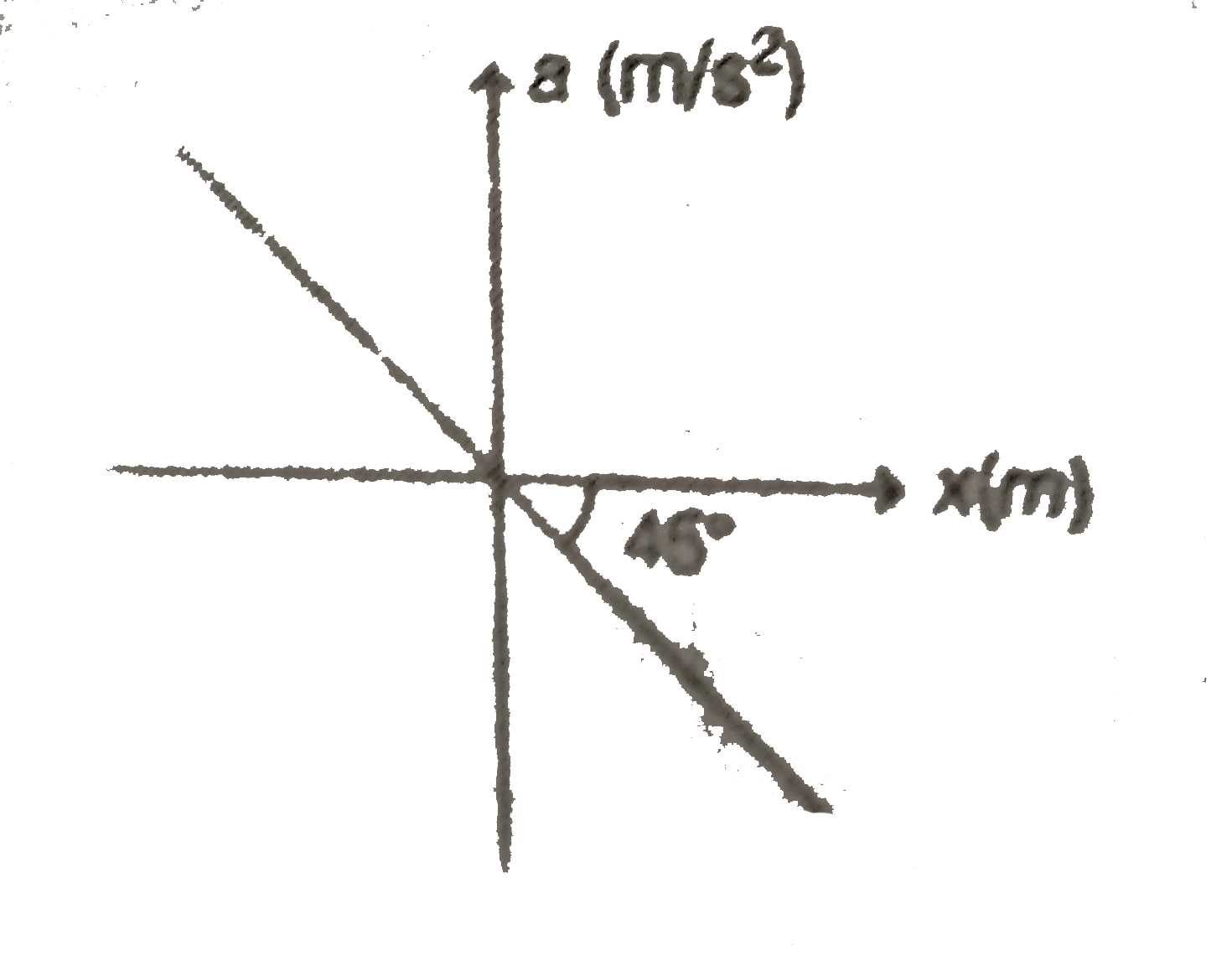
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
View SolutionThe maximum speed of a particle executing SHM is 10 m/s and maximum acceleration is 31.4m//s^(2) . Its periodic time is
View SolutionThe acceleration of a particle executing SHM is at a distance of from the mean position. Calculate its time period.
View SolutionA particle executing SHM, covers a displacement of half of amplitude in one second. Calculate its time period.
View SolutionIf the maximum velocity and acceleration of a particle executing SHM are equal in magnitude the time period will be
View SolutionIf the maximum velocity and acceleration of a particle executing SHM are equal in magnitude, the time period will be
View SolutionA body executing has a maximum velocity of and a maximum acceleration of . Its time period of oscillation is
View SolutionA particle of mass 2kg executing SHM has amplitude 20cm and time period 1s. Its maximum speed is
View SolutionA particle of mass 2kg executing SHM has amplitude 20cm and time period 1s. Its maximum speed is
View SolutionA particle executes along a straight line long. When the displacement is its velocity and acceleration are numerically equal. The time period of is
View SolutionA particle is executing SHM with time period T. If time period of its total mechanical energy isT' then is
View SolutionA particle is executing SHM with time period T. If time period of its total mechanical energy isT' then (T')/(T) is
View SolutionA particle executes SHM with a time period T . The time period with which its potential energy changes is
View SolutionA particle is executing SHM with an amplitude of 2 m. The difference in the magnitudes of its maximum acceleration and maximum velocity is 4. The time period of its oscillation is
View Solution