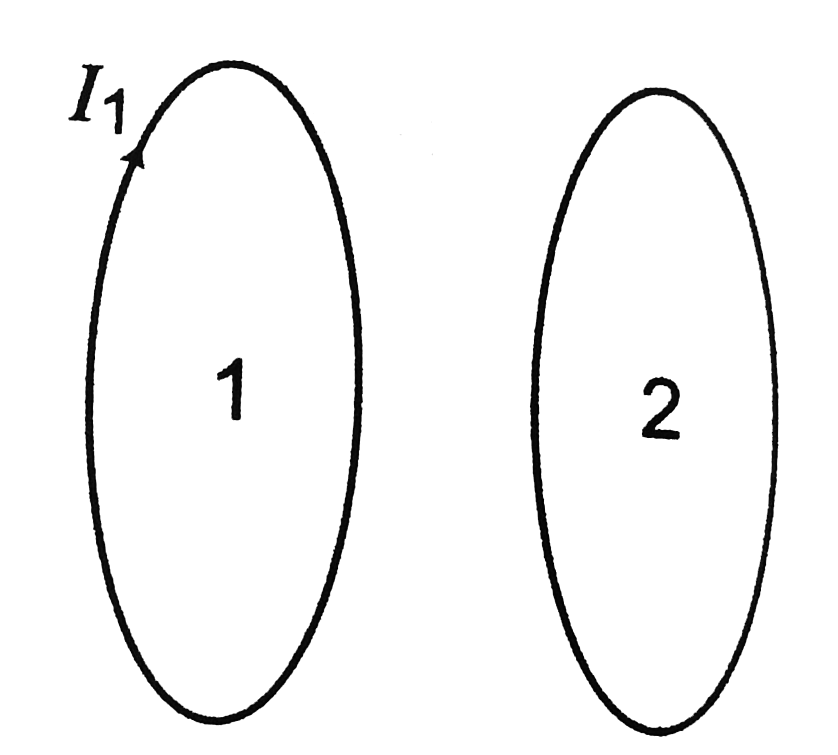Example Type 1 from DC PANDEY ENGLISH ELECTROMAGNETIC INDUCTION for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| DC PANDEY ENGLISH | Example Type 1 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
A coil consists of 200 turns of wire having a total reistance of 2.0Ω. Each turn is a square of side 18cm, and a uniform magnetic field directed perpendicular to the plane of the coil is turned on. If the field changes linearly from 0 to 0.5t in 0.80s, what is the magnitude of induced emf and current in the coil while the field is changing?View SolutionQuestion 11
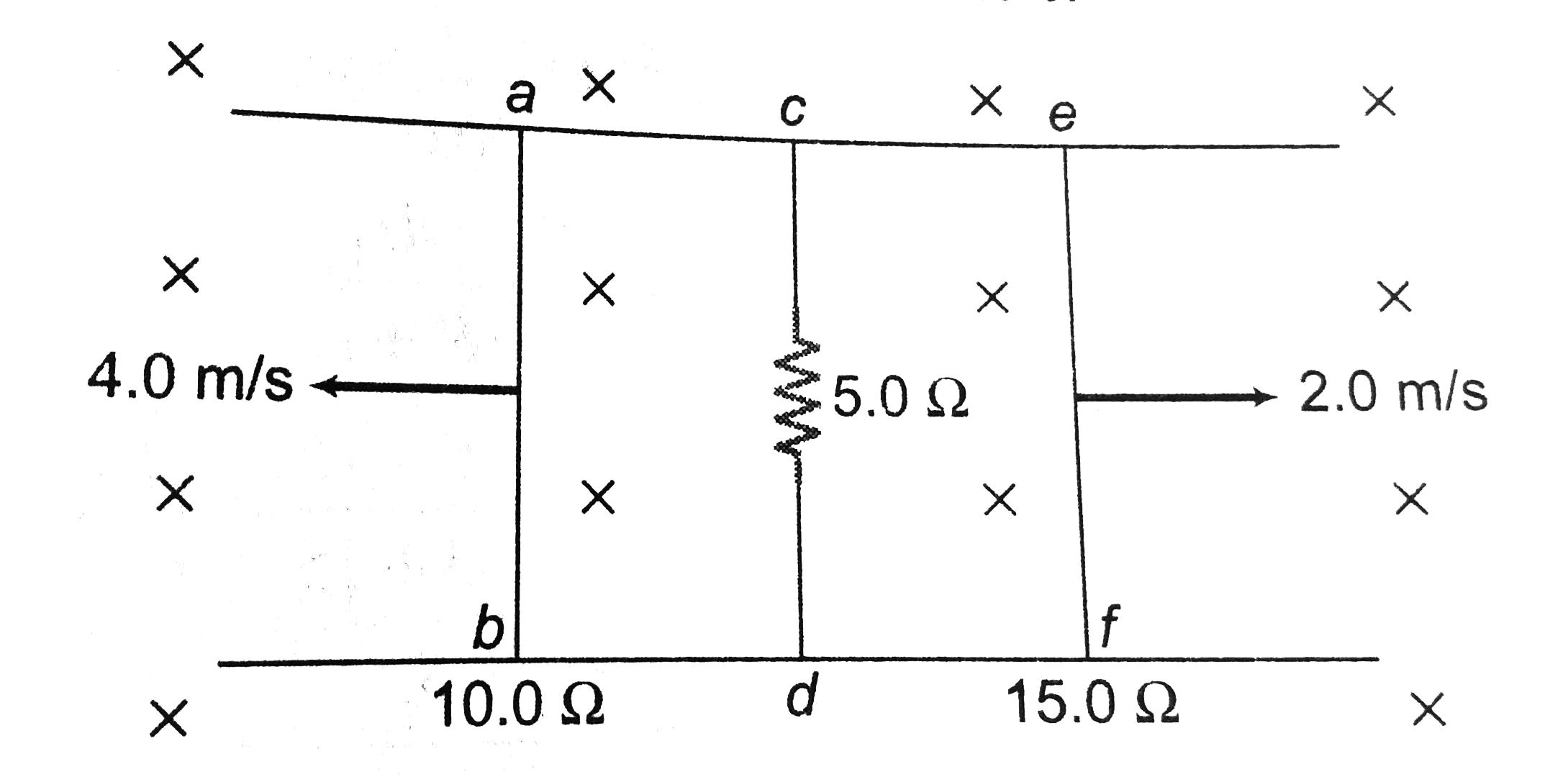
Two parallel rails with negligible resistance are 10.0cm apart. The are connected by a 5.0Ω resistor. The circuit also contains two metal rods having resistances of 10.0Ω and 15.0Ω along the rails. The rods are pulled away from the resistor at constant speeds 4.00ms and 2.00m/s respectively. A uniform magnetic field of magnitude 0.01T is applied perpendicular to the, plane of the rails. Determine the current in the 5.0Ω resistor.
 View Solution
View SolutionQuestion 12
Figure shows the to views of a rod that can slide without friction. The resistor is 6.0Ω and a 2.5T magnetic field is directed perpendicularly downward into the paper. Let l=1.20m.

a. Calculate the force F required to move the rod to the right at a constant speed of 2.0ms,
b. At what rate is energy deliered to the resistor?
c. Show that this rate is equal to the rate of work done by the applied force.View SolutionQuestion 20
Two solenoids A and B spaced close to each other and sharing the same cylindrical axis have 400 and 700 turns, respectively. A current of 3.50A in coil A produced an average flux of 300μT−m2 through each turn of A and a flux of 90.0mT−m2 through each turn of B.
a. Calculate the mutual inductance of the two solenoids.
b.What is the self inductance of A?
c. What emf is induced in B when the current in A increases at the rate of 0.5A/s?View SolutionQuestion 23
A capacitor of capacitance 25μF is charged to 300V. It is then connected across a 10mH inductor. The resistance in the circuit is negligible.
a. Find the frequency of oscillation of the circuit.
b. Find the potential difference across capacitor and magnitude of circuit current 1.2ms after the inductor and capacitor are connected.
c. Find the magnetic energy and electric energy at t=0 and t=1.2ms. View SolutionQuestion 24
The magnetic field at all points within the cyllindrical region whose cross section is indicated in the accompanying Figure starts increasing at a constant rate α. T/s. find the magnitud of electric field as a function of r, the distance from the geometric centre of the region. View Solution
View SolutionQuestion 26
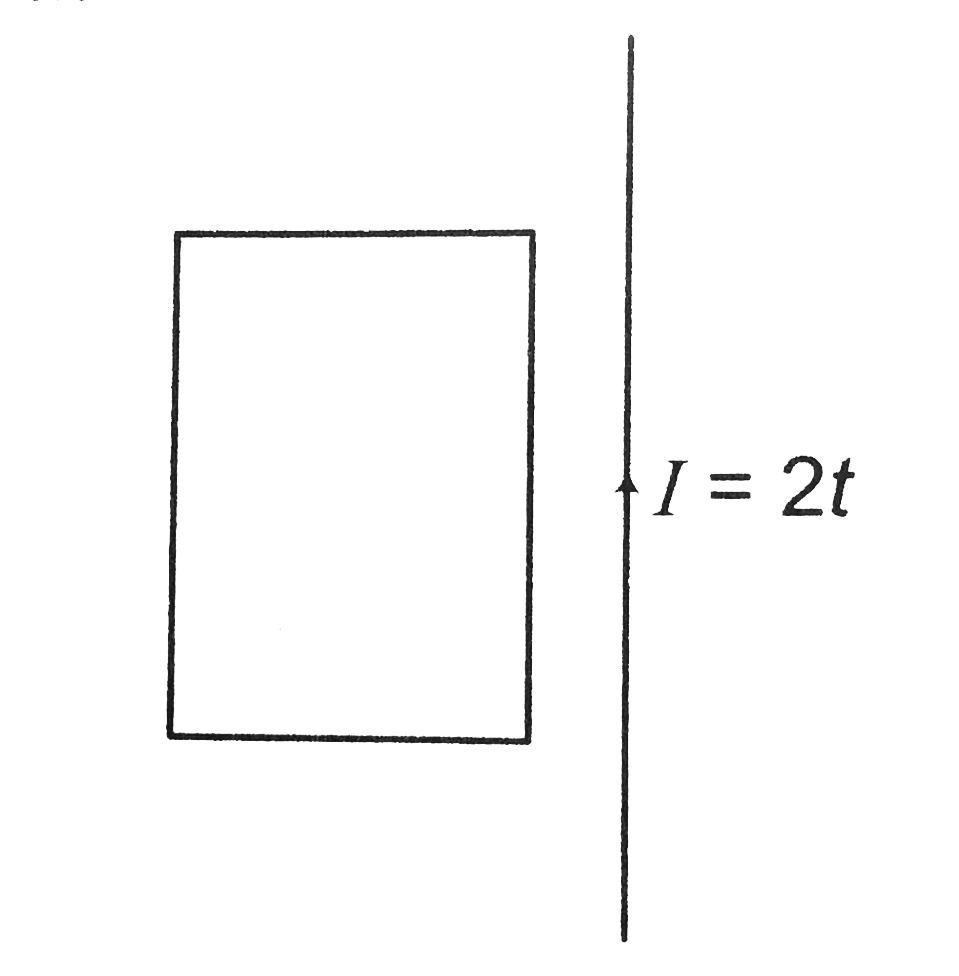
Current in a long current carrying wire is I=2t
A conducting loop is placed to the right of this wire. Find
a. magnetic flux ϕB passing through the loop.
b. induced emf|e| prodced in the loop.
c. if total resistance of the loop is R, then find induced current Iin in the loop.View SolutionQuestion 27
A constant current I flows through a long straight wire as shown in figure. A square loop starts moving towards righ with as constant speed v.
a Find induced emf produced i the loop as a function x
b. If total resistance of the loop is R, then find induced current in the loop, View SolutionQuestion 29
Two different coils have self inductances L1=9mH and L2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coils is the same. At that time, the current the induced voltage and the energy stored in the first coil are i1,V1 and W1 respectively.
Corresponding values for the second coil at the same instant are i2,V−2 and W2 respectively. Then,View SolutionQuestion 32
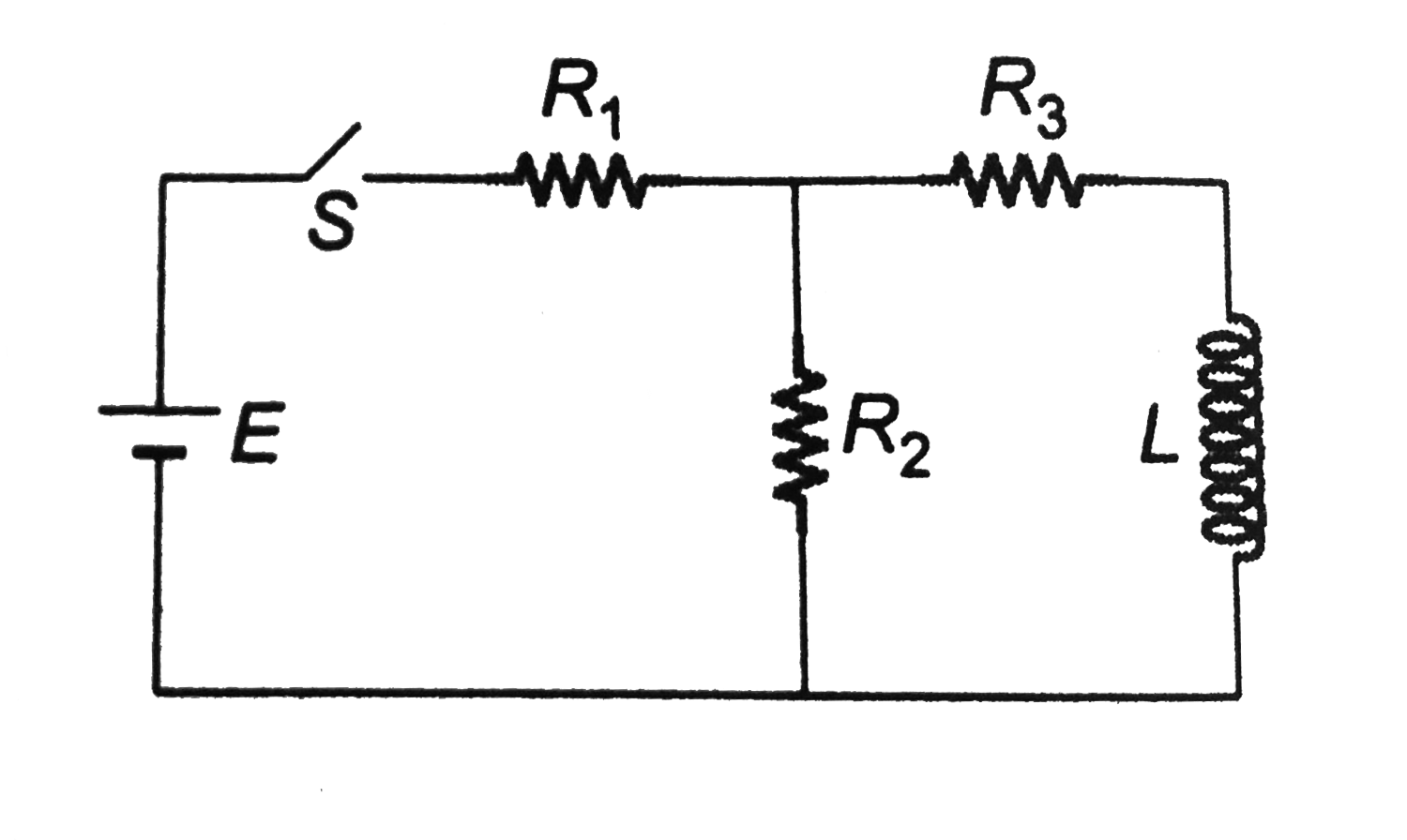
An inductor of inductance L=400mH and resistors of resistances R1=2Ω and R2=2Ω are connected to a battery of emf E=12V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t=0.
What is the potential dro across L s a function of time? After the steady state is reached, the switch is opened. What is the direction ad the magnitude of current throough R1 as a function of time?View SolutionQuestion 34
A circuit containing a two position switch S is shown in figure
a. The switch S is in position 1. Find the potential differecne VA−VB and the rte of production of joule heat in R1
b. If now the switch S is put in position 2 at t=0. Find ltbRrgt i steady current in R4 and ii hte time when current in R4 is half the steady value. Also calculate the energy stored in the inductor L at that time.View SolutionQuestion 36
An inductor of inductance 2.0mH s connected across a charged capacitor of capacitance 5.0μF and the resulting LC circuit is set oscillating at its natural frequency. Let Q denote the instantaneous charge on the capacitor and I the current in the circuit. It is found that the maximum value of charge Q is 200μC.
a. When Q=100μC, what is the value of ∣∣∣dIdt∣∣∣?
b. When Q=200μC, what is the value of I?
c. Find the maximum value of I.
d. When I is equal to one-half its maximum value, what is the value of |Q|? View SolutionQuestion 38
The magnetic field B at all points within a circular region of the radius R is uniform space and directed into the plane of the page in figure. If the magnetic field is increasing at a rate dB/dt what are the magnitude and direction of the force on as stationary positive point charge q located at points a,b,c? (Point a is a distance r above the centre of the region, point b is a distance r to the right to the centre and point c is at the centre of the region).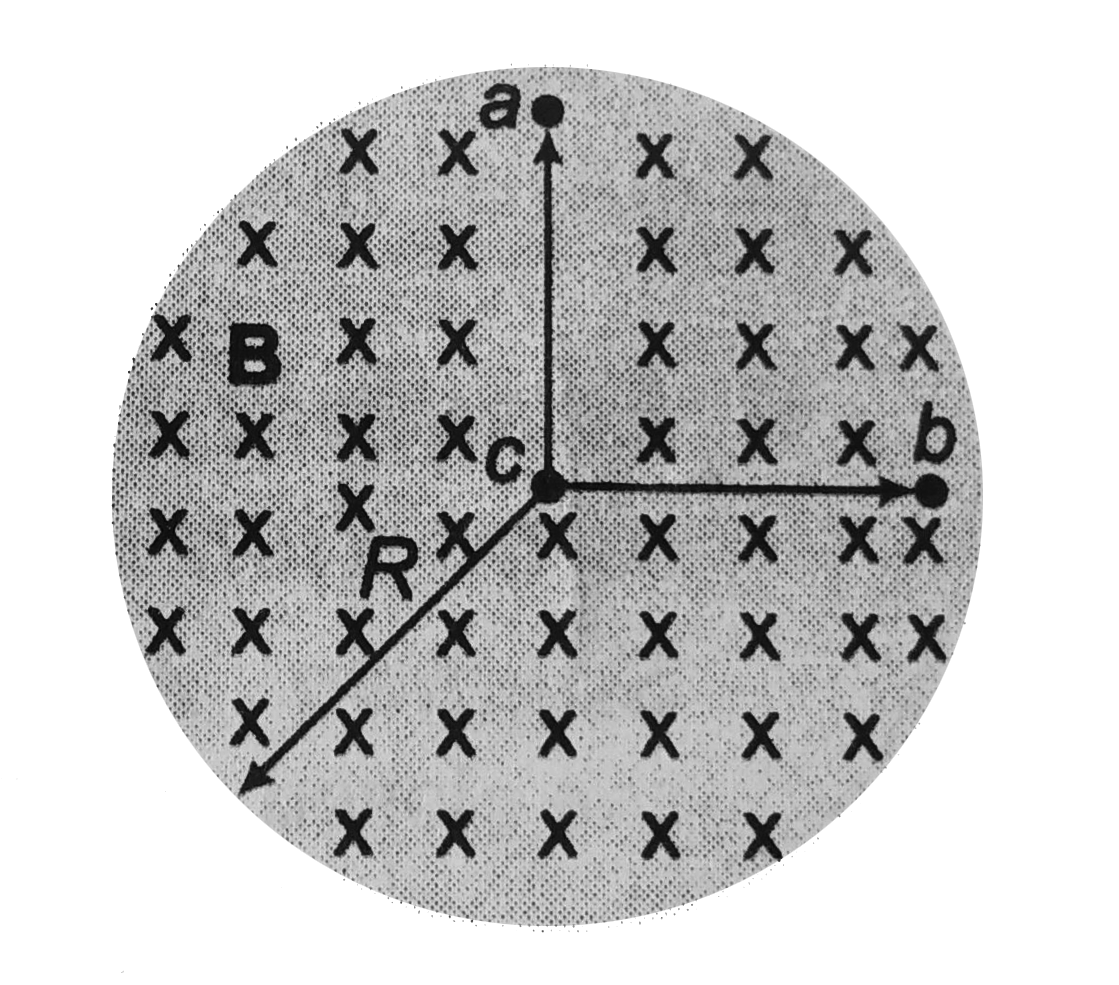 View Solution
View SolutionQuestion 40
A pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m tied to the other end of the string hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate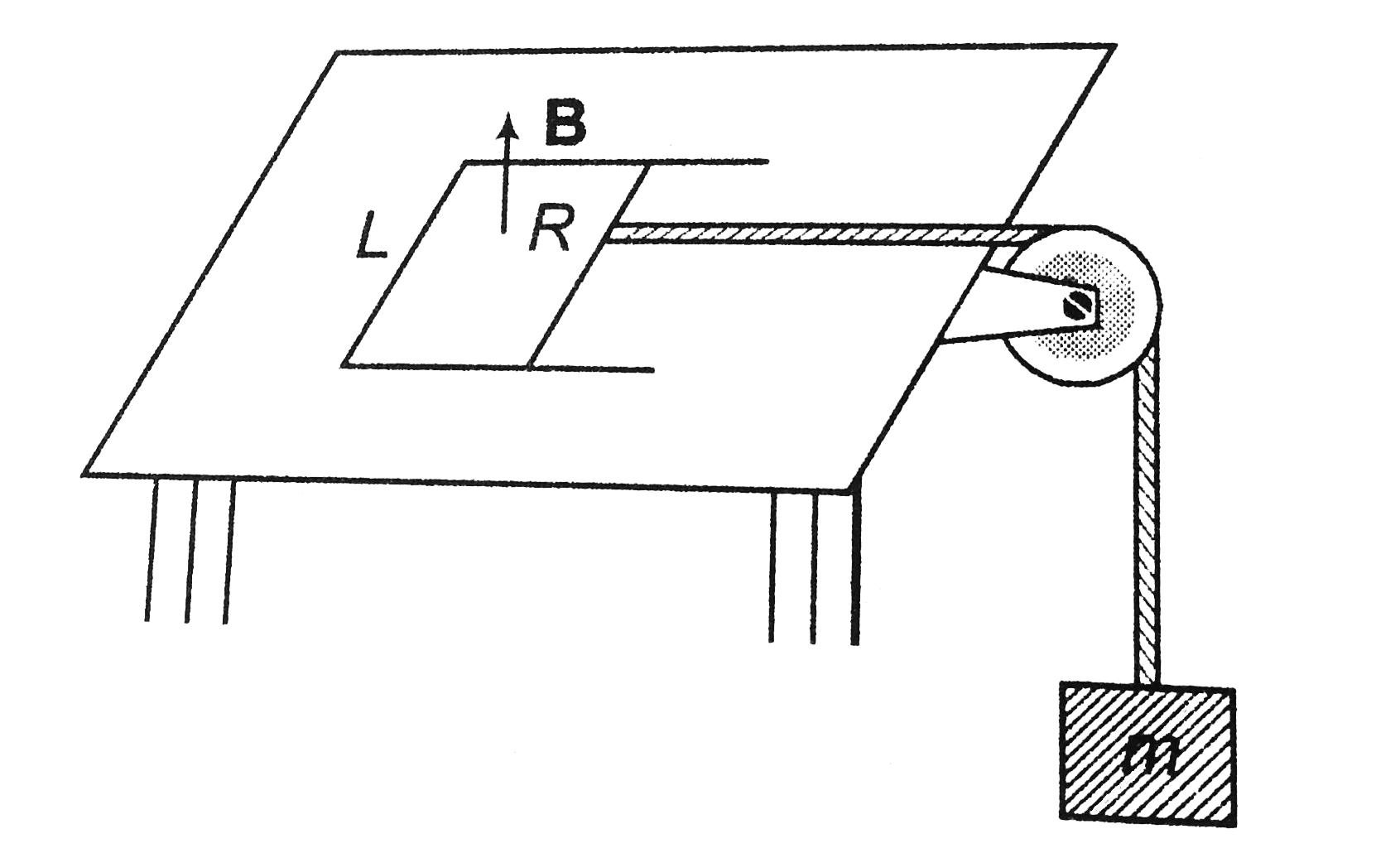
a. the terminal velocity achieved by the rod and
b. The acceleration of the mass of the instant when the velocity of the rod is half the terminal velocity.View SolutionQuestion 41
A loop is formed by two parallel conductors connected by a selenoid with inductance L and a condutcing rod of mass which can freely (without friction) slide over the conductors. The conductors are located in a horizontal plane in as uniform vertical magnetic field B.The distance between the conductors is l.
At the moment t=0 the rod is impart the initial velocity v0 directed to the right. find the equation of its motion d(t) if the electric resistance of the loop is negligibleView SolutionQuestion 42
A sensitive electronic device of resistance 175Ω is to be connected to a source of emf by a switch. The device is designed to operate with a current of 36mA but to avoid damage to the device, the current can rise to no more than 4.9mA in the first 58μs after the switch the closed. To protect the device it is connected in series with an inductor.
a. What emf must the source have?
b. What inductance is required?
c. What is the time constant?View SolutionQuestion 43
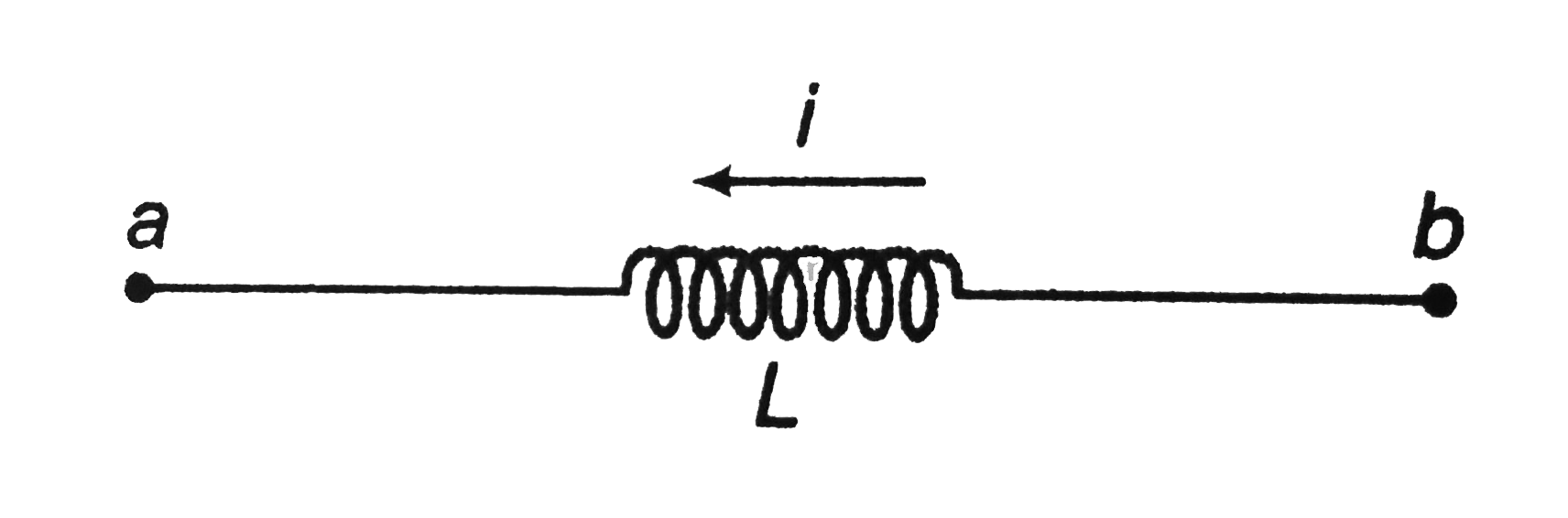
A conducting rod shown in figure of mass m and length l moves on two frictionless horizontal parallel rails in the presence of a unifom magnetic field directed into the page., The rod is given an initial velocity v0 to the right and is released at t=0. Find s a function of time
a. the volocity of the rod
b. the induced current and
c. the magntitude of the induced emf.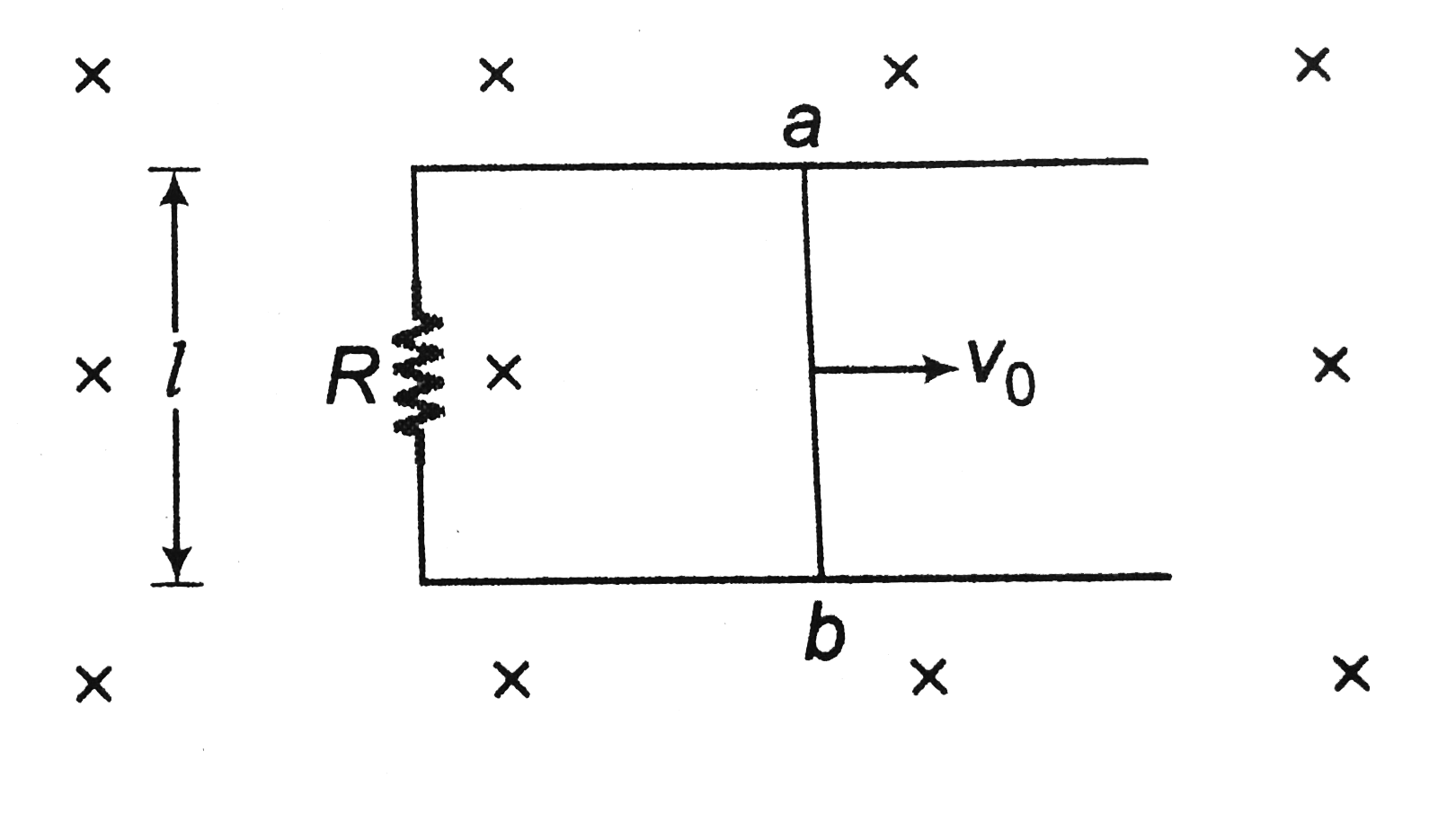 View Solution
View SolutionQuestion 44
A wire loop enclosing as semicircle of radius R is located on the boudary of uniform magnetic field B. At the moment t=0, the loop is set into rotation with a costant angular acceleration α about an axis O coinciding with a line of vector B on the boundary. Find the emf induced in the loop as a function of time. Draw the approximate plot of this function.The arrow in the figure shows the emf direction taken to be positive.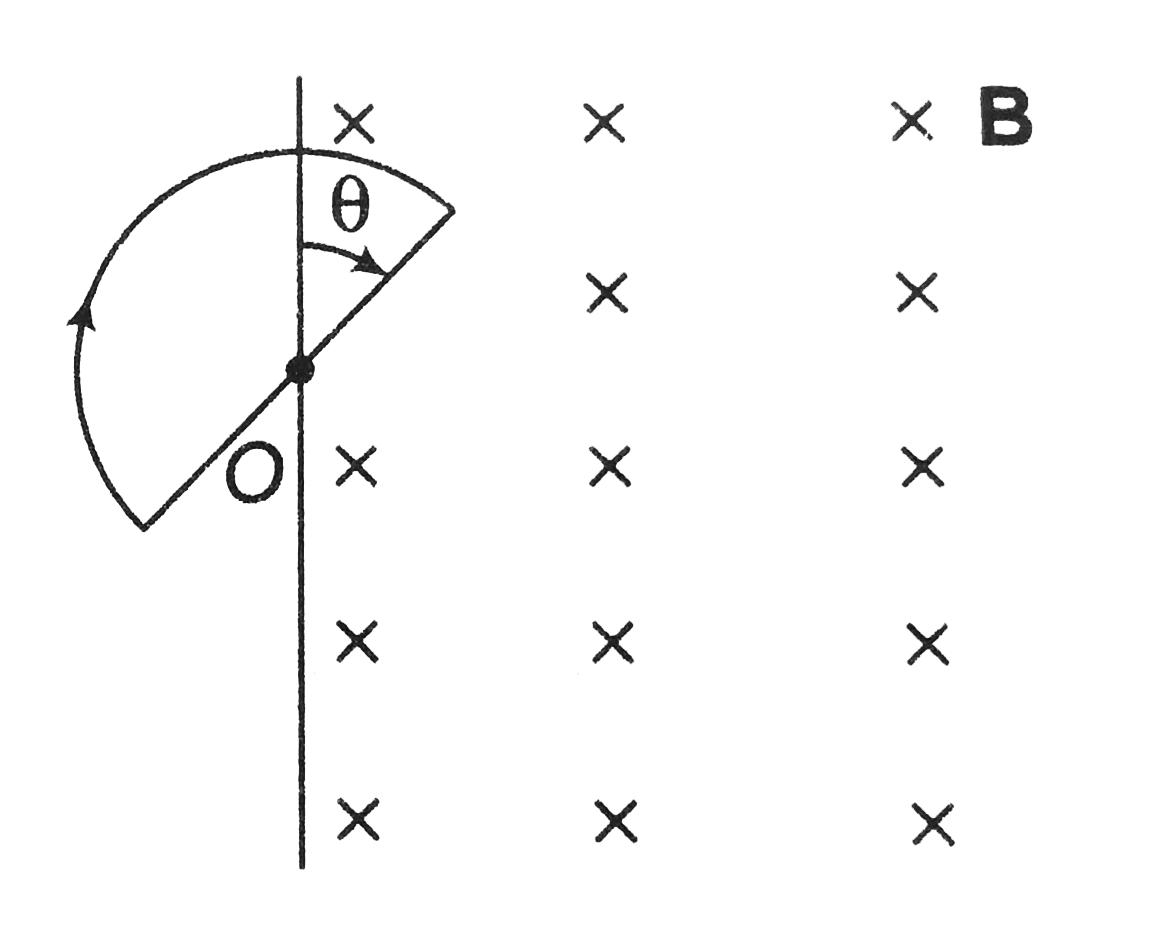 View Solution
View SolutionQuestion 45
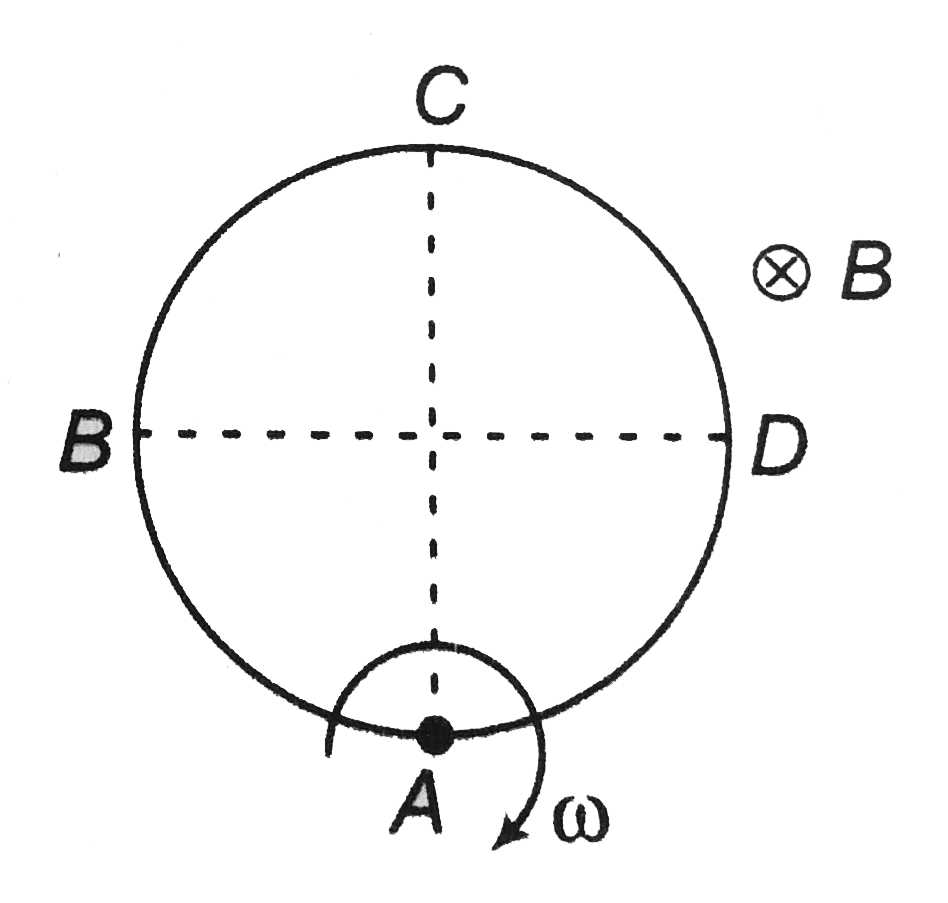
A uniform wire of resistance per unit length λ is bent into semicircle of radius a. The wire rotates with angular velocity ω in a vertical plane about a orizontal is passing through C. A uniform magnetic field B exists in space in a direction perpendicular to paper inwards.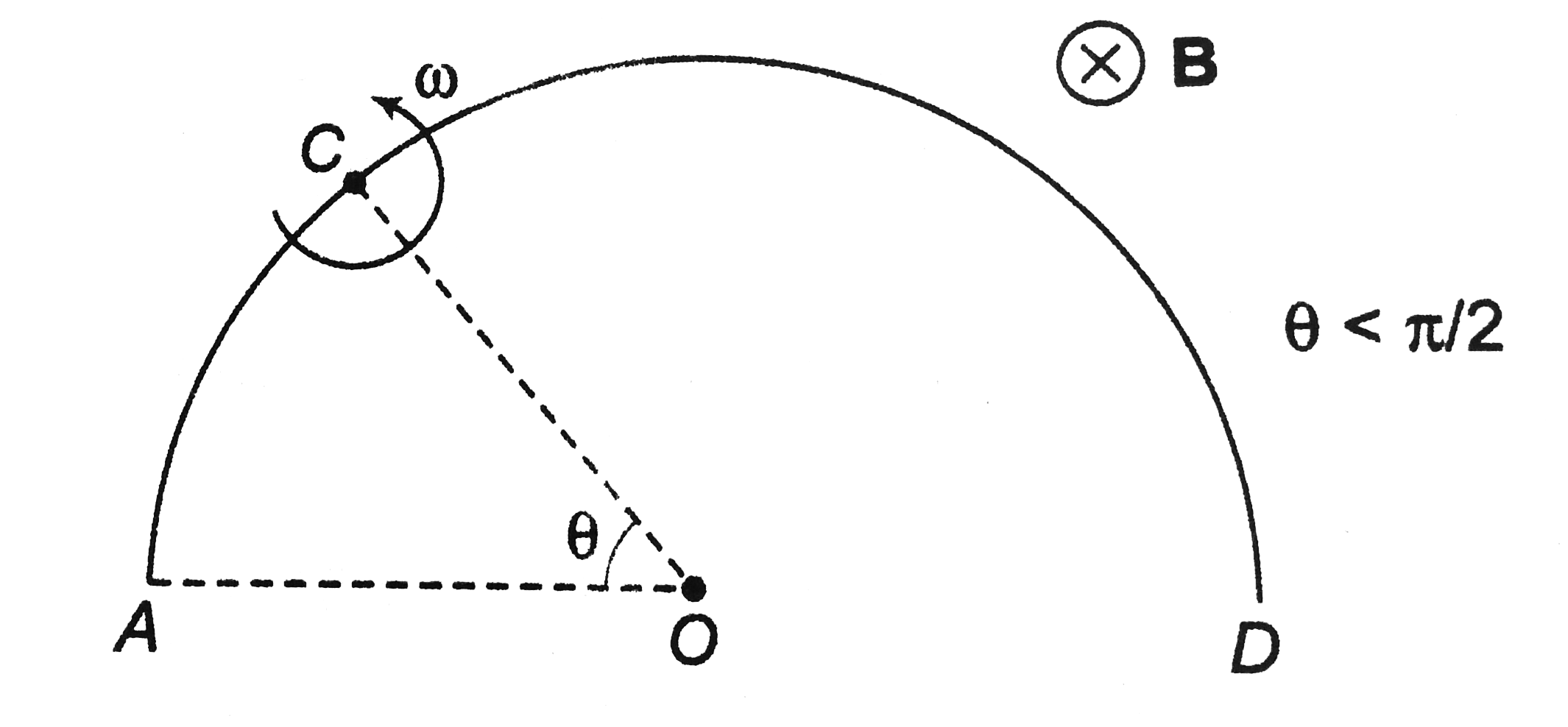
a. Calculate potential difference between points A and D. which point is at higher potential?
b. If points A and D are connected by a conducting wire of zero resistance, find the potential difference between A and C.View SolutionQuestion 46
A battery of emf E and of negligible internal resistance is connected in a L−R circuit as shown in figure. The inductor has a piece of soft iron inside it. When steady state is reached in the piece of soft iron is abruptly pulled out suddenly so that the inductance of the inductor decreases to nL with n<1 with battery remaining connected. Calculate.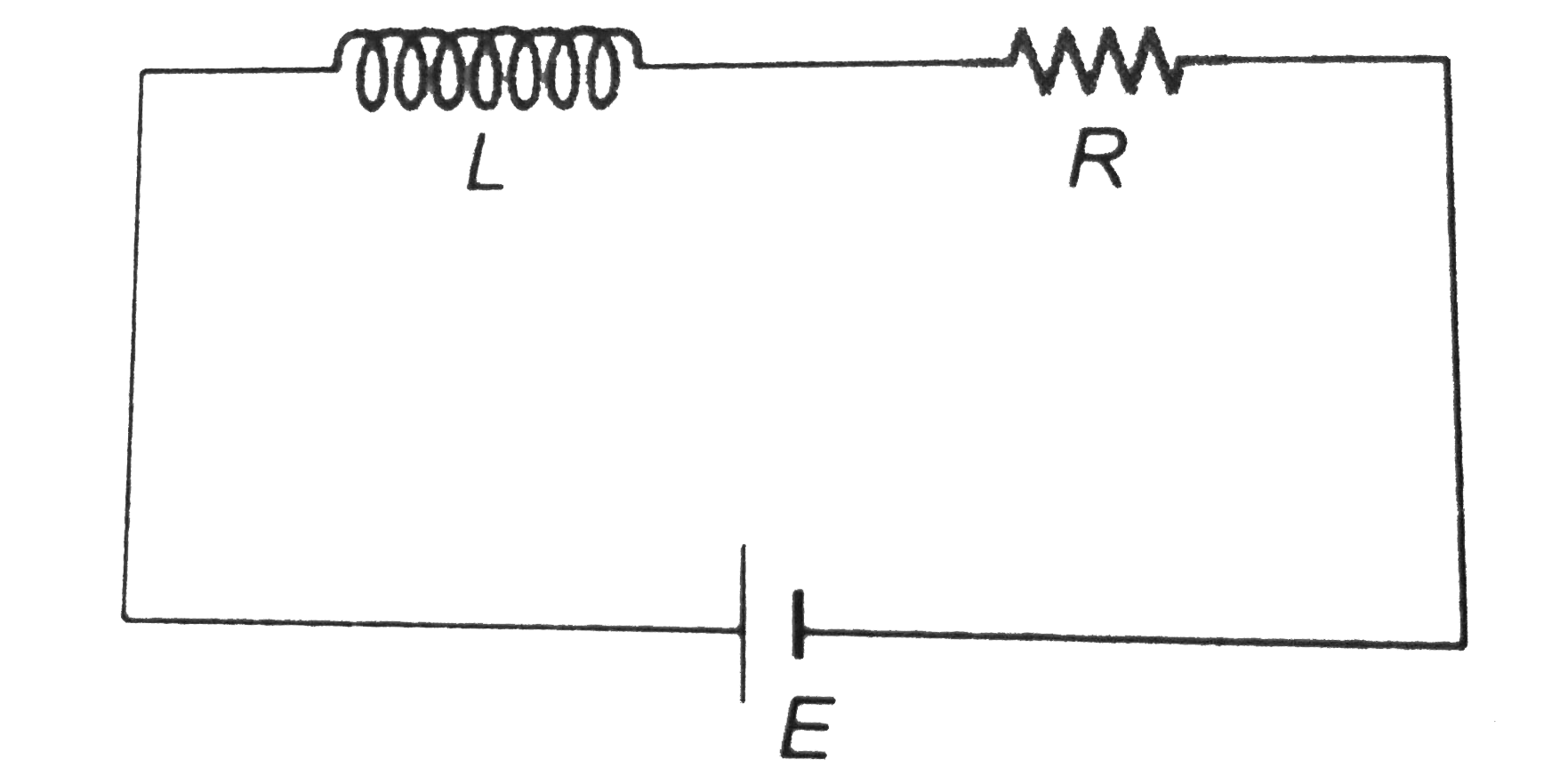
a. Current as a function of time assuming t=0 at the instant when piece is pulled.
b. the work done to pull out the piece.
c. thermal power generated in the circuit as as function of time.
d. power supplied by the battery as a function of time.
HOW TO PROCEED When the inductance of an inductor is abruptly changed, the flux passing through it remains constant.
ϕ= constant
∴Li= constant (L=ϕi) View Solution
All Exercises from DC PANDEY ENGLISH Class 12 PHYSICS ELECTROMAGNETIC INDUCTION
- CHECK POINT
- EXERCISE 27.1
- EXERCISE 27.2
- EXERCISE 27.3
- EXERCISE 27.4
- EXERCISE 27.5
- EXERCISE 27.6
- EXERCISE 27.7
- LEVEL 1 ASSERTION AND REASON
- LEVEL 1 OBJECTIVE
- LEVEL 1 SUBJECTIVE
- LEVEL 2 COMPREHENSION BASED
- LEVEL 2 MORE THAN ONE CORRECT
- LEVEL 2 SINGLE CORRECT
- LEVEL 2 SUBJECTIVE
- MATCH THE COLUMNS
- MEDICAL ENTRANCE SPECIAL FORMAT QUESTIONS
- MEDICAL ENTRANCES GALLERY
- OBJECTIVE QUESTIONS
- SUBJECTIVE TYPE
- TAKING IT TOGETHER
- EXAMPLE
- EXAMPLE TYPE 1
- EXAMPLE TYPE 2
- EXAMPLE TYPE 3
- EXAMPLE TYPE 4
- EXAMPLE TYPE 5
- EXAMPLE TYPE 6
- MISCELLANEOUS EXAMPLES