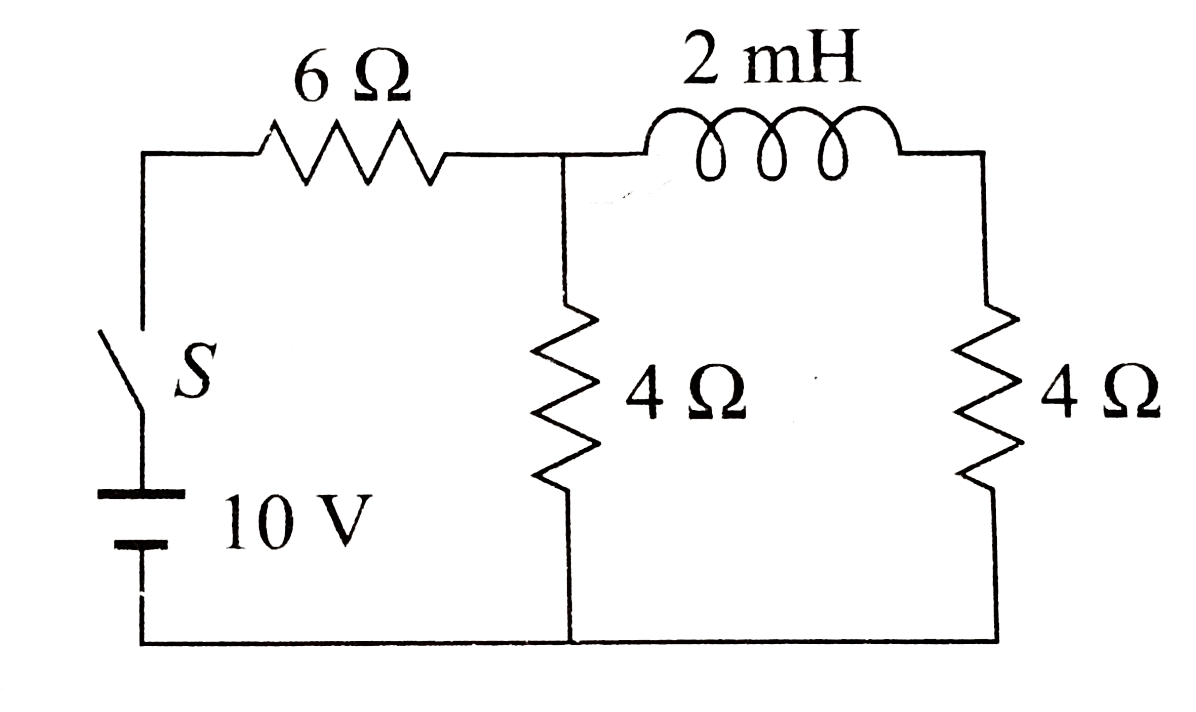Integer from CENGAGE PHYSICS (ENGLISH) MISCELLANEOUS VOLUME 5 for Class 12
| Class 12 | PHYSICS |
| Chapter | MISCELLANEOUS VOLUME 5 |
| CENGAGE PHYSICS (ENGLISH) | Integer |
| Medium | English |
| Academic Year | 2023-2024 |
Question 6
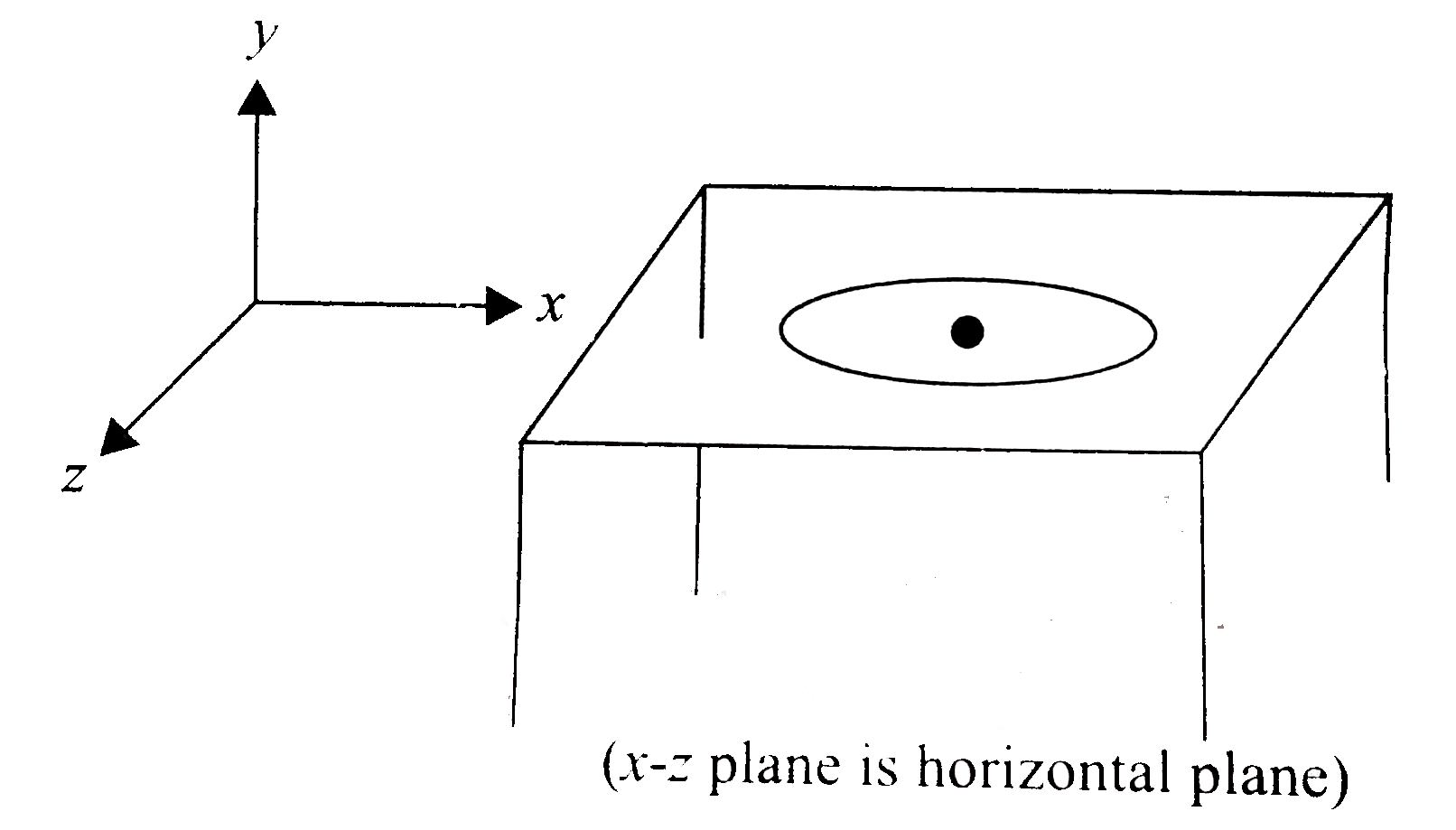
In a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point( 2a, b/2, 0) its speed becomes 2v. Find the value of electric field strength in term of m, v and co-ordinates.View SolutionQuestion 8
An (α)-particle and a proton are both simultaneously projected in opposite direction into a region of constant magnetic field perpendicular to the direction of the field. After some time it is found that the velocity of the (α)-particle has changed in a direction by 45∘. Then at this time, the angle between velocity vectors of (α)-particle and proton isView SolutionQuestion 11
A uniform magnetic field B and electric field E exist along y and negative z axis respectively. Under the influence of these field a charge particle moves along OA undeflected. If electric field is switched off, find the pitch of helical trajectory in which the particle will move.
 View Solution
View SolutionQuestion 18
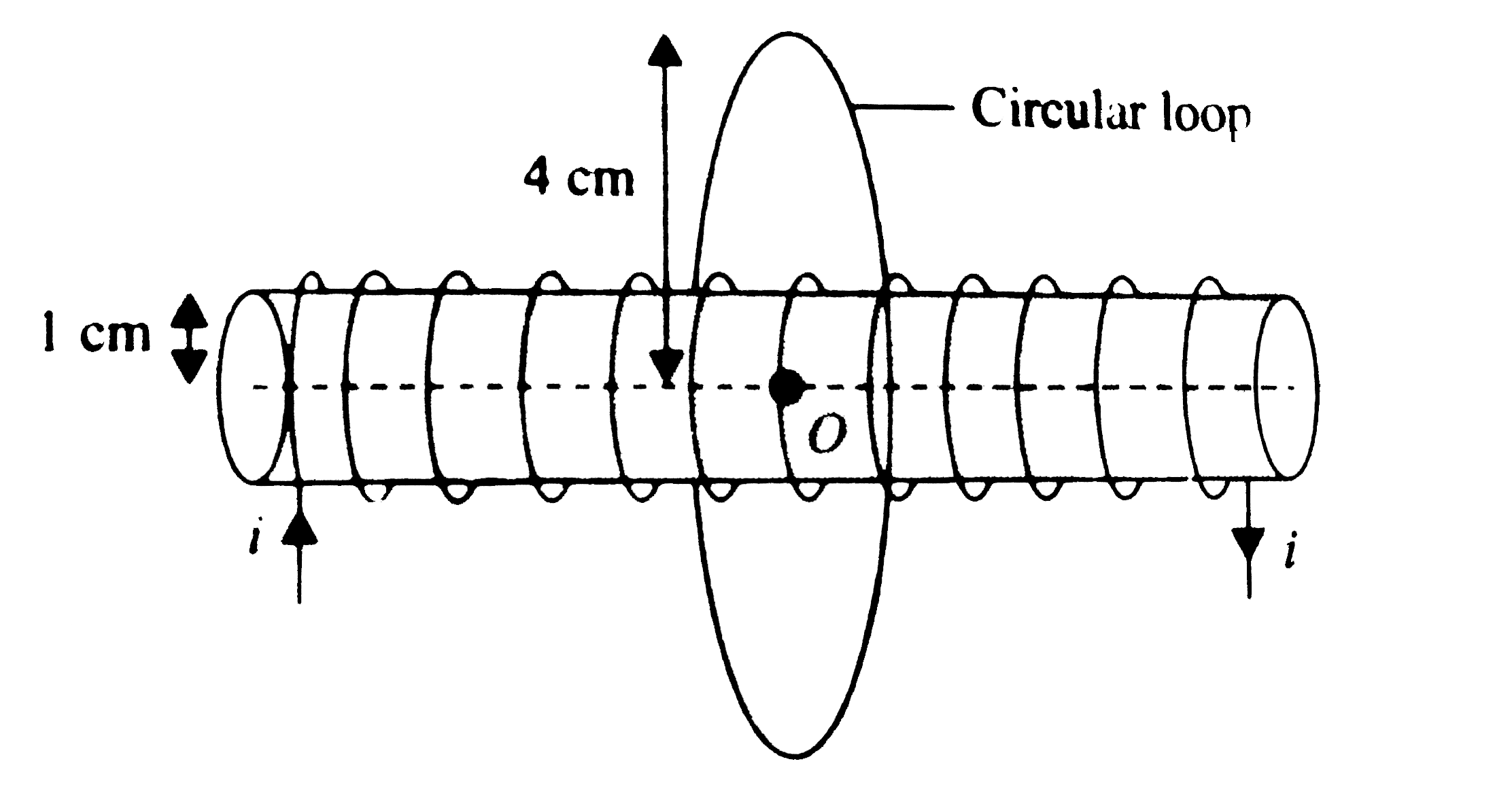
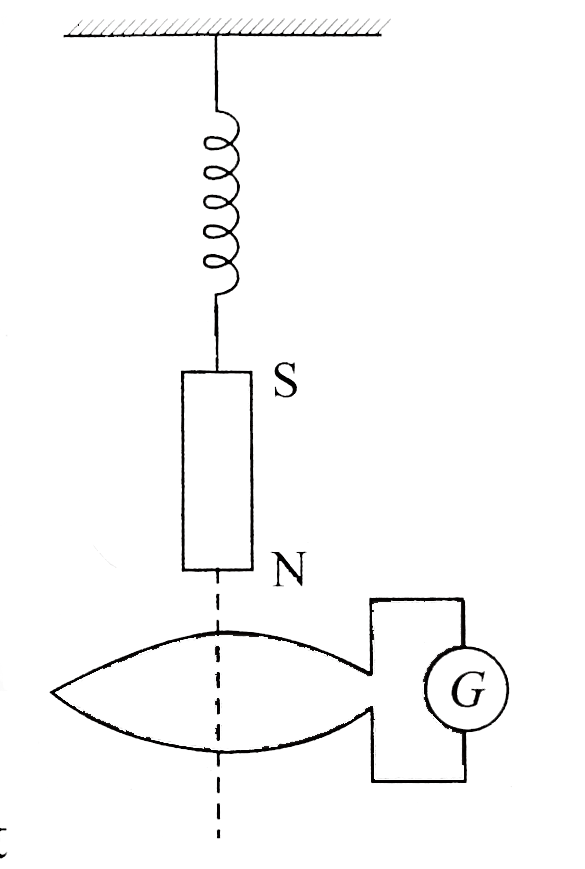
In Fig (a) and (b), two air-cored solenoids P and Q have been shows. They are placed near each other. In Fig (a), when IP, the current in P, changes at the rate of 5As−1, an emf of 2mV is induced in Q. The current in P is then switched off, and the current changing at 2As−1 is fed through Q as shows in the figure. What emf will be induced in P?

 View Solution
View SolutionQuestion 20
A triangular wire frame (each side =2m) is placed in a region of time variant magnetic field dB/dt=(√3)T/s. The magnetic field is perpendicular to the plane of the triangle and its centre coincides with the centre of triangle. The base of the triangle AB has a resistance 1(Ω) while the other two sides have resistance 2(Ω) each. The magnitude of potential difference between the points A and B will be
 View Solution
View SolutionQuestion 26
A plane loop is shaped as two squares (Fig) and placed in a uniform magnetic field at right angle to the loop's plane. The magnetic induction varies with time as B=B0sin(ω)t,whereB0=10mTand(ω)=100rads−1. The wires do not touch at point A. If resistance per unit length of the loop is 50m(Ω)/m, then amplitude of current induced in the loop is
 View Solution
View SolutionQuestion 27
Two infinitely long thin , insulated,straight wires lie in the x-y plane along the x and y axes, respectively.Each wire carries a current /respectively, in the positive x direction and positive y - direction.The magntic field will be zero at all points on the straight line with equation View SolutionQuestion 29
Two infinitely long straight parallel wire are 5 m apart, perpendicular to the plane of paper. One of the wires, as it passes perpendicular to the plane of paper, intersects it at A and carries current I in the downward direction. The other wire intersects the plane of paper at point B and carries current k int the outward direction O in the plane of paper as shown in Fig. With x and y axis shown, magnetic induction at O in the component form can be expressed as
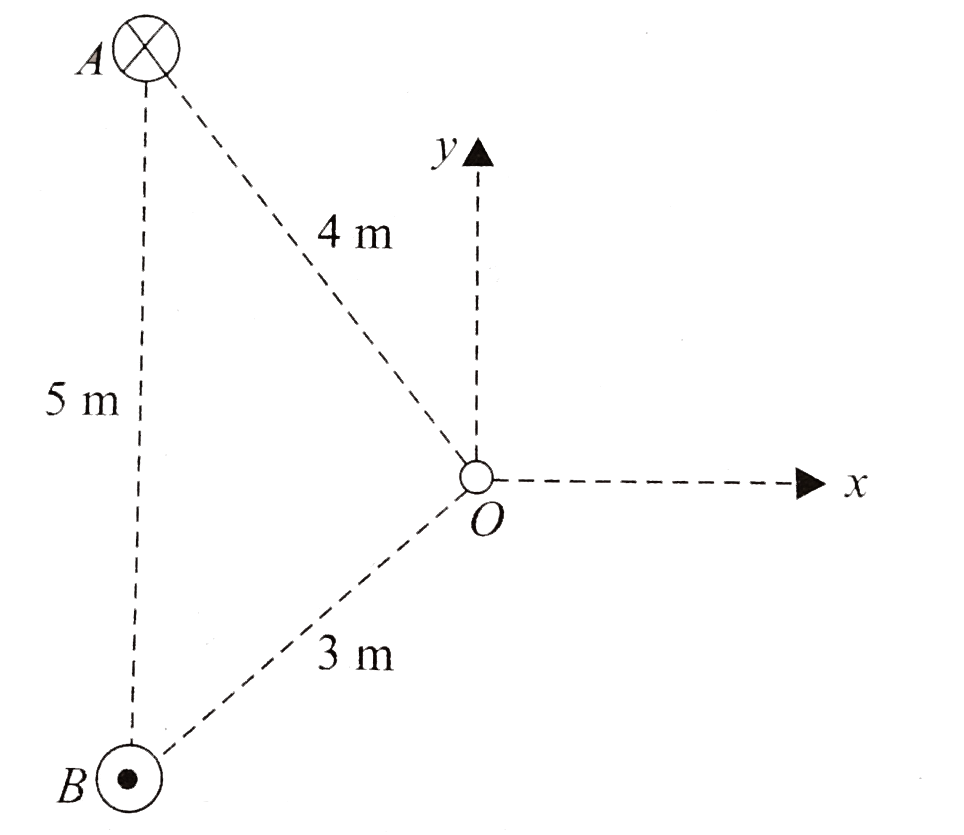 View Solution
View SolutionQuestion 30
In Fig. , AB is a non-conducting rod. Equal charges of magnitude q are fixed at various points on the rod as shown. The rod is rotated uniformly about an axis passing through O and perpendicular to its length such that linear speed at the end A or B of the rod is 3ms−1. Magnetic field at O is
 View Solution
View SolutionQuestion 31
Infinite wires, each carrying a current 0.5 A, are kept parallel to y-axis and intersecting x-axis at x=±1 m, +02m, ±4m, ±8m etc. Wires kept at positive values of x carry current in the same direction while wires kept at negative values of x carry current successively in opposite directions as shown in Fig.
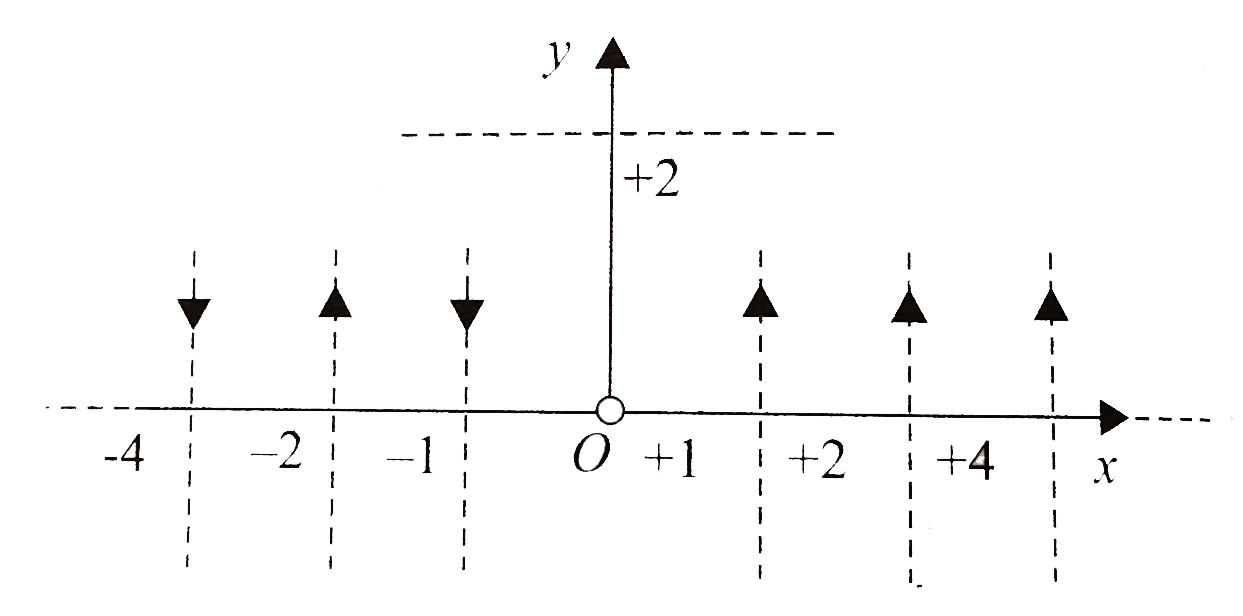
A wire is kept parallel to x-axis and intersecting y-axis at y=2 m. It carries a current i. Assuming this wire to be insulated from others then the current i in it such that magnetic induction at O is zero is
(assuming each wire to be infinitely long)View SolutionQuestion 32
Three infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
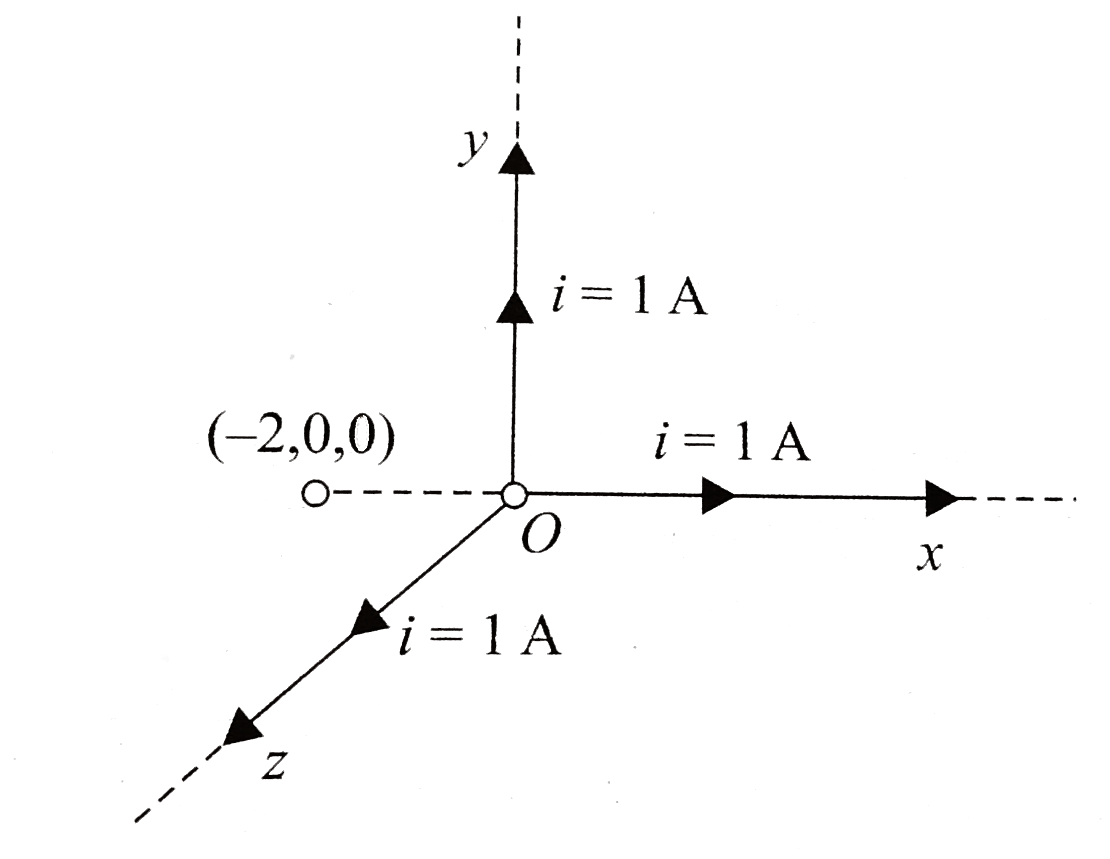 View Solution
View SolutionQuestion 39
AB and AC are boundary lines within which a magnetic field B exists. If the magnetic field is absent, a charged particle of mass m and charge q must have passed through a point P on angle bisector of -BAC, at a distance r(√2) from A, if it has fallen on AB normally at a point Q such that QP =r. If the magnetic field is present, how much time the charged particle will take to come out of the magnetic field
 View Solution
View SolutionQuestion 40
Two recangular plates A and B placed at a distance 2a apart, are connected to a battery to produce an electric field. There are insulators between plantes C and other two plates. A magnetic field exists along z-axis. A charged particle of mass m and charge q passes through a hole at the middle of the plate A with velocity v and strikes at Q which is the middle of the bottom edge of plate B after passing through a hole inplate C. If E=mv2/qa, what will be the speed of the particle at Q?
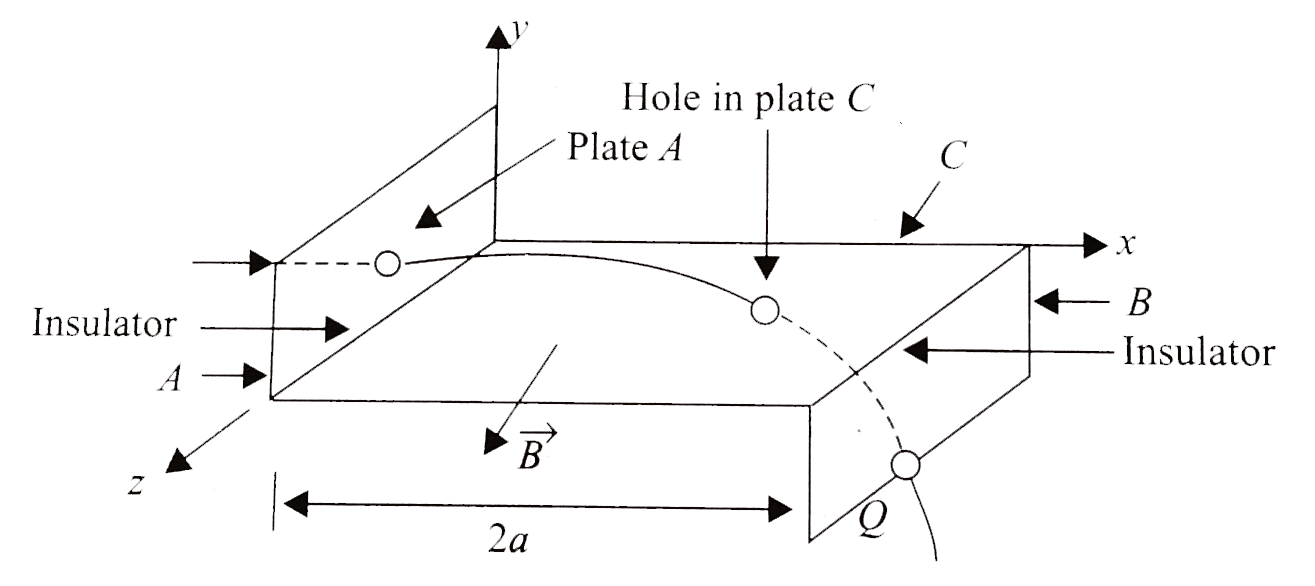 View Solution
View SolutionQuestion 41
A magnetic field B exists between OA and OB. Inclined at an angle (θ), a charged particle strikes at point A on surface OA, at a distance (2Kcos(θ))(qvB) from O, where K is kinetic energy, q is the charge and v is the velocity of the particle. At what angle with horizontal (measured from end B) will the charged particle emerge from OB?
 View Solution
View SolutionQuestion 42
To the right of line PQ is a uniform magnetic field →B.B1A is the line of incidence of a charged particle, which comes out of the field along DE, CA and DF are the normals at A and D. −B1AC=(θ). Angle measured from CA in clockwise direction is taken as positive. What will be the value of (θ) so that angle subtended by the part of the circle (along which charged particle moves in the field) at its centre and facing the circle is less than π?
 View Solution
View SolutionQuestion 47
A triangular system of mass 100 gm consisting of 3 wires of length, as shown in Fig and length of AO as 4 units, are placed in the magnetic field of 1T. The current of 1 A flows through wire AO. The wires are of same material and cross-sectional area. In which direction will the system move?
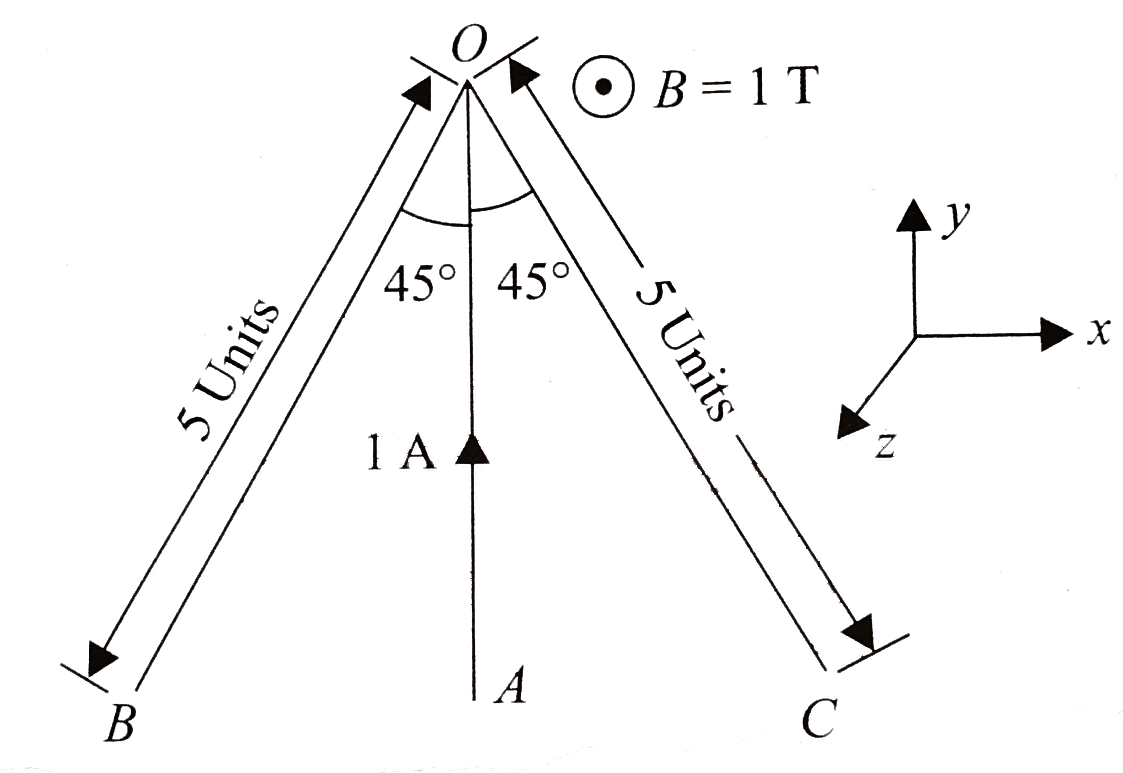 View Solution
View SolutionQuestion 52
A wire loop is placed in a region of time varying magnetic field which is oriented orthogonally to the plane of the loop as shown in Fig. The graph shows the magnetic field variation as the function of time. Assume the positive emf is the one which drives a current in the clockwise direction and seen by the observer in the direction of B. Which of the following graphs best represents the induced emf as a function of time?
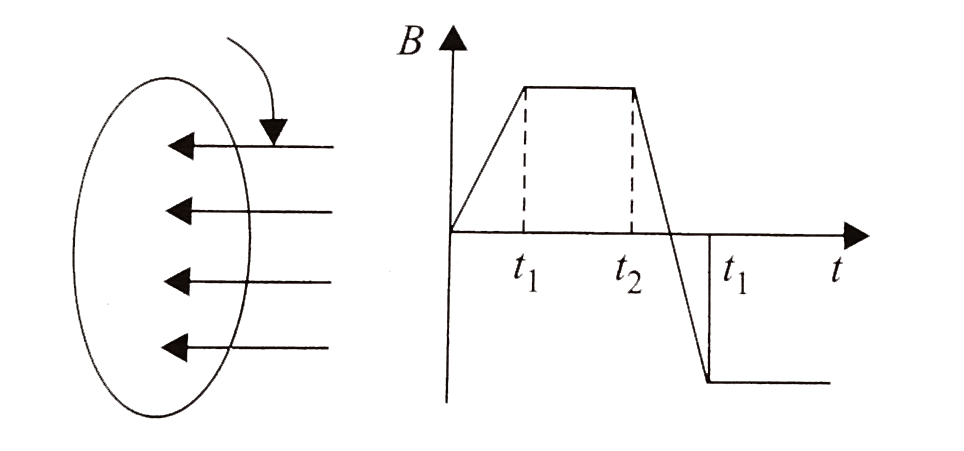 View Solution
View SolutionQuestion 54
Figure shows an isosceles triangle wire frame with apex angle equal to (π)/2. The frame starts entering into the region of uniform magnetic field B with constant velocity v at t =0. The longest side of the frame is perpendicular to the direction of velocity. If i is the intantaneous current through the frame then choose the alternative showing the correct variation of i with time.
 View Solution
View SolutionQuestion 57
Fig. Shows a conducting circular loop of radius a placed in a uniform, perpendicular magnetic field B. A thick metal rod OA is pivoted at the centre O. The other end of the rod touches the loop at A. The centre O and a fixed point C on the loop are connected by a wire OC of resistance R. A force is applied at the middle point of the rod OA perpendicularly, so that the rod rotates clockwise at a uniform angular velocity (ω). Find the force.
 View Solution
View SolutionQuestion 58
Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed (ω) as shown in the figure. Find the current in the rod when −AOC=90∘View SolutionQuestion 59
Consider a variation of the previous problem. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistance but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity (ω) in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it.
Find the magnitude of this force when the rod makes an angle (θ) with the vertical.View SolutionQuestion 60
Figure shows a situation similar to the previous problem. All parameters are the same except that a battery of emf ε and a variable resistance R are connected between O and C. The connecting wires have zero resistance. No external force is applied on the rod (except gravity, forces by the magnetic field and by the pivot).

In what way should the resistance R be changed so that the rod may rotate with uniform angular velocity in the clockwise direction? Express your answer in terms of the given quantities and the angle (θ) made by the rod OA with the horizontal.View SolutionQuestion 71
A current I=3.36(1+2t)×10−2 A increase at a steady state in a long staight wire. A small circular loop of radius 10−3 m has its plane parallel to the wire and is placed at a distance of 1 m from the wire. The resistance of loop is 8.4×10−4(Ω). Find the approximate value of induced current in the loop.View SolutionQuestion 74
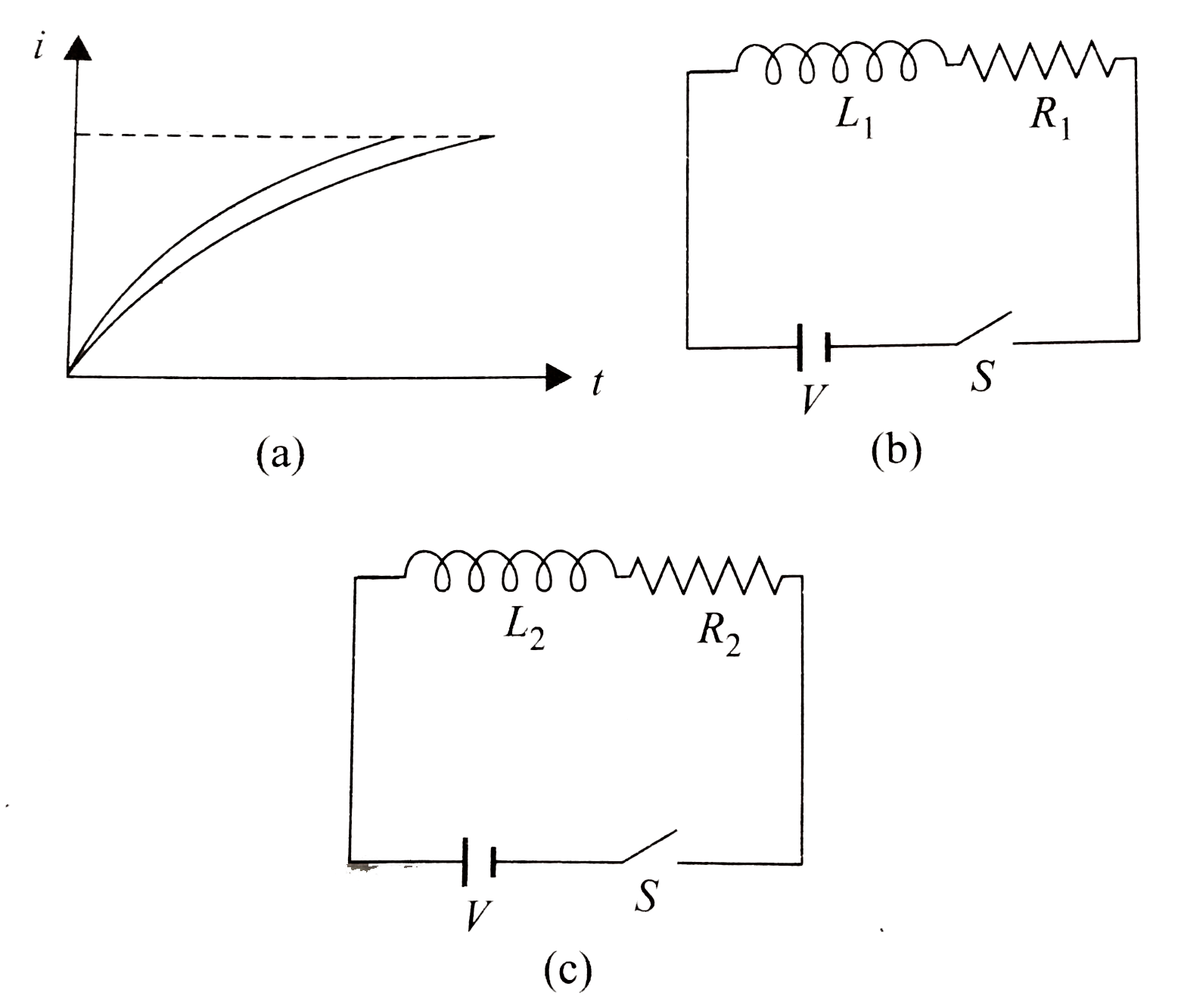
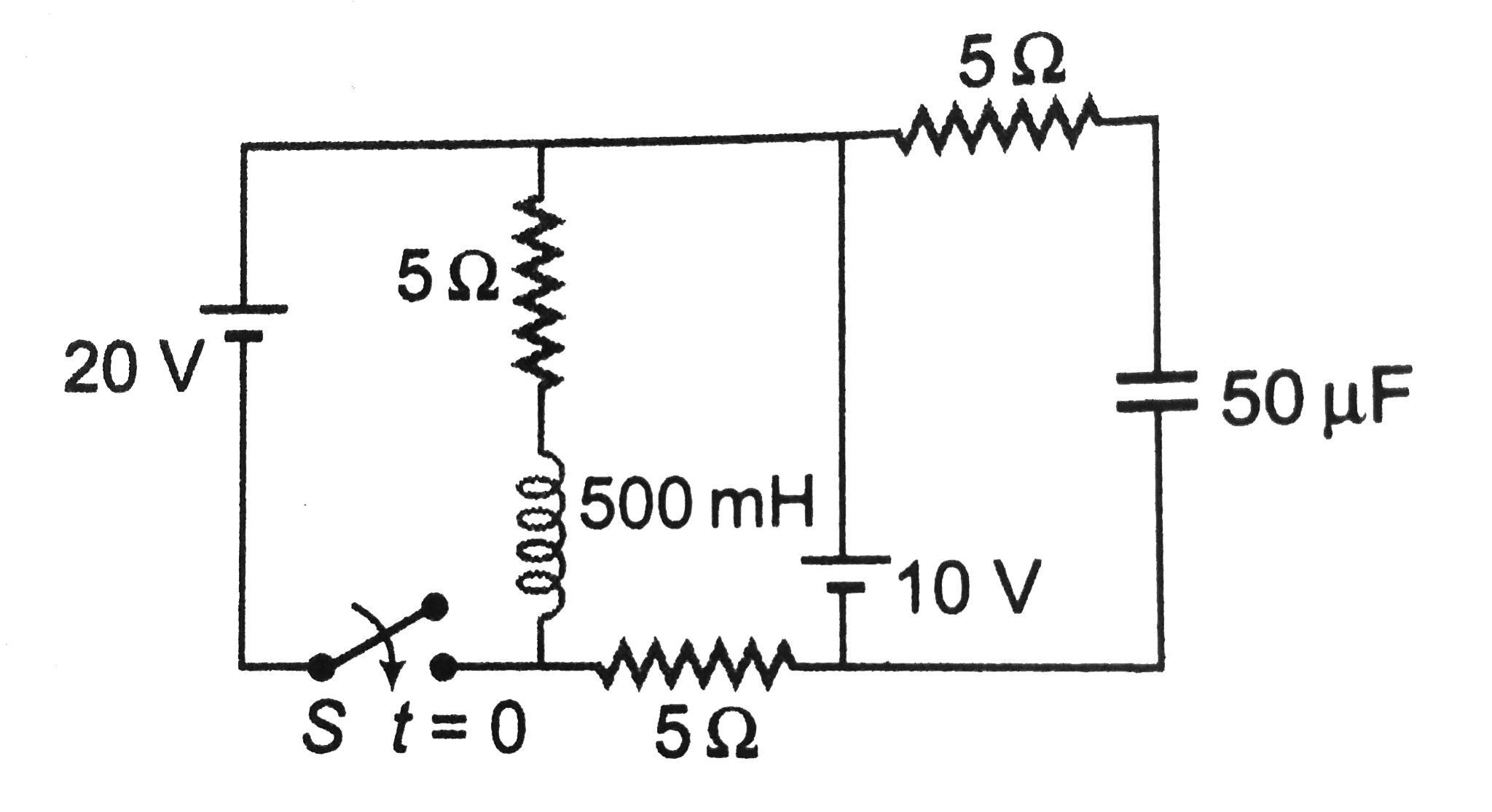
In the circuit shown in fig, the time constant of the two braches are equal(=T). Then if the key S is closed at the instant t=0, the time in which the current in the circuit through the battery will rise to its final value of (E/R) will be, (assume that the internal resistance of the battery and of the connecting wire are negligible)
 View Solution
View SolutionQuestion 75
A particle of charge +Q and mass M is projected with velocity v in the plane of paper. Above the dark line magnetic field is (B1) and below it is (B2) both perpendicular to the plane of paper. Which can be the possible path on which the charge will move? (Consider all possible cases for values of (B1)and(B_2))
 View Solution
View SolutionQuestion 85
The diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
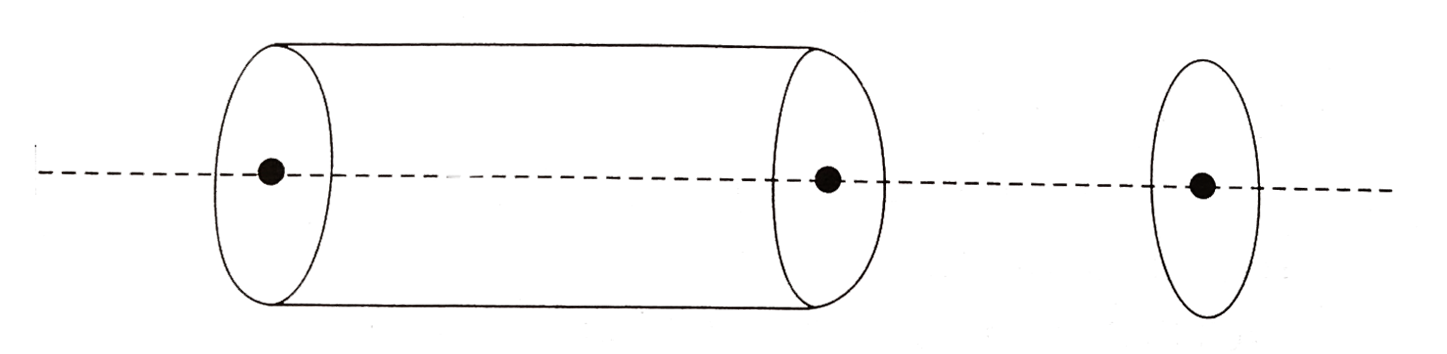 View Solution
View SolutionQuestion 86
An inverted L shaped conductor PRQ is made by joining two perpendicular conducting rods, each of length 1.5 L, at end R. This structure is moving in x-y plane containing variable magnetic field →B=−3xˆe(k) with a velocity vˆe(i)+vˆj. If potential of P is Vp and that of Q is VQ, then value of VP−V(Q) at the instant when P is at origin as shown in Fig. Will be
 View Solution
View SolutionQuestion 87
Consider parallel conducting rails separated by a distance l. There exists a uniform magnetic field B perpendicular to the plane of the rails as shown in Fig. Two conducting wires each of length l are placed so as to slide on parallel conducting rails. One of the wires is given a velocity v0 parallel to the rails. Till steady state is achieved, loss in kinetic energy of the system is
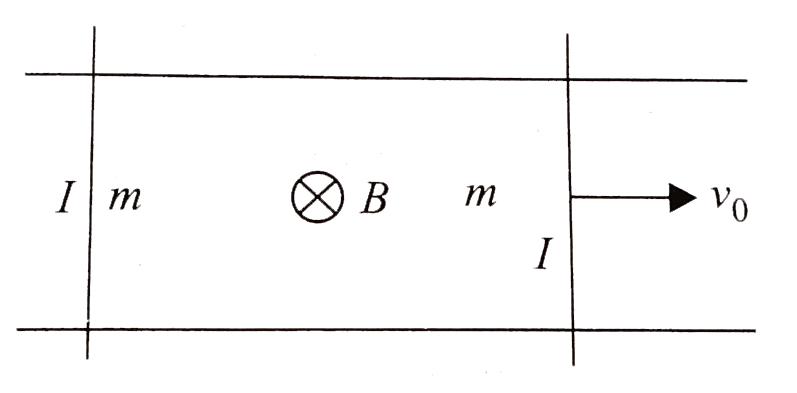 View Solution
View SolutionQuestion 88
A system consists of two coaxial current carrying circular loops as shown in Fig. The self inductance of loop 1 is L1 and self inductance of loop 2 is L2. Magnitude of mutual inductance is M. If at any instant current flowing through loop 1 and loop 2 are i1andi2 respectively, then total magnetic energy of the system is
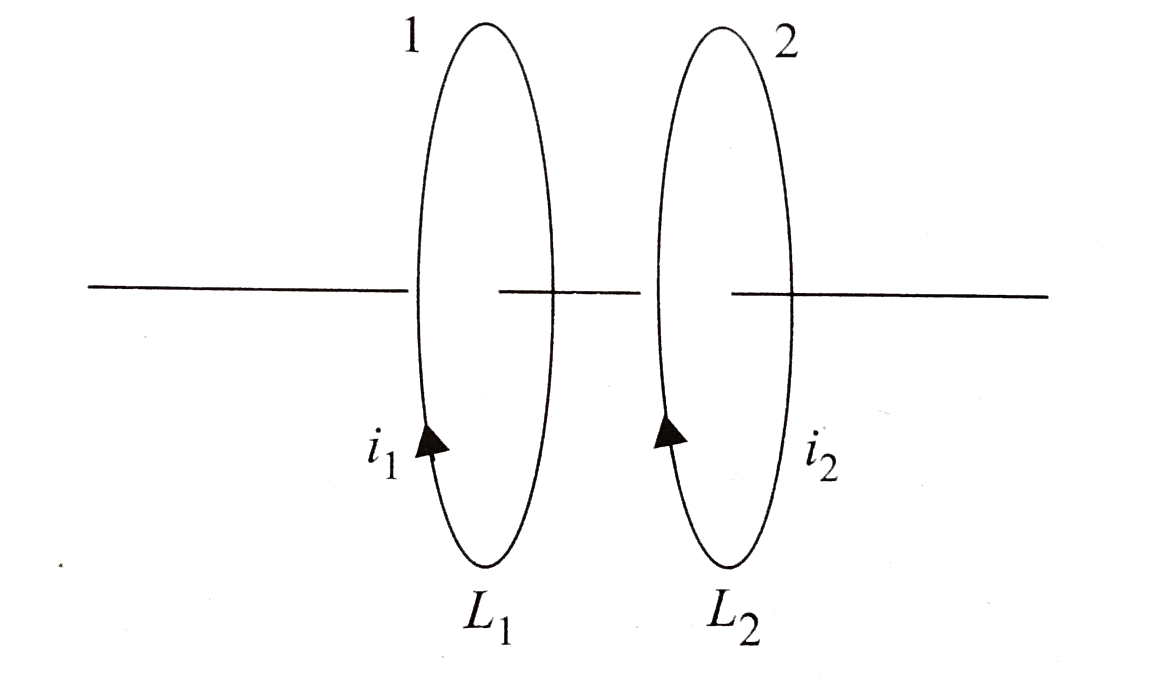 View Solution
View SolutionQuestion 89
A conducting rod of length 1 is moving on a horizontal smooth surface. Magnetic field in the region is vertically downward and magnitude B0. If centre of mass (COM) of the rod is translating with velocity v0 and rod rotates about COM with angular velocity v0/l, then potential difference between points O and A will be
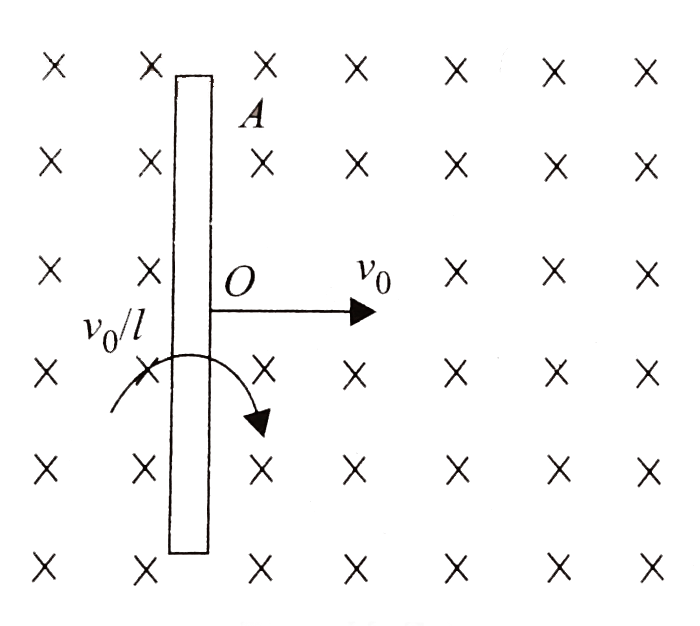 View Solution
View SolutionQuestion 90
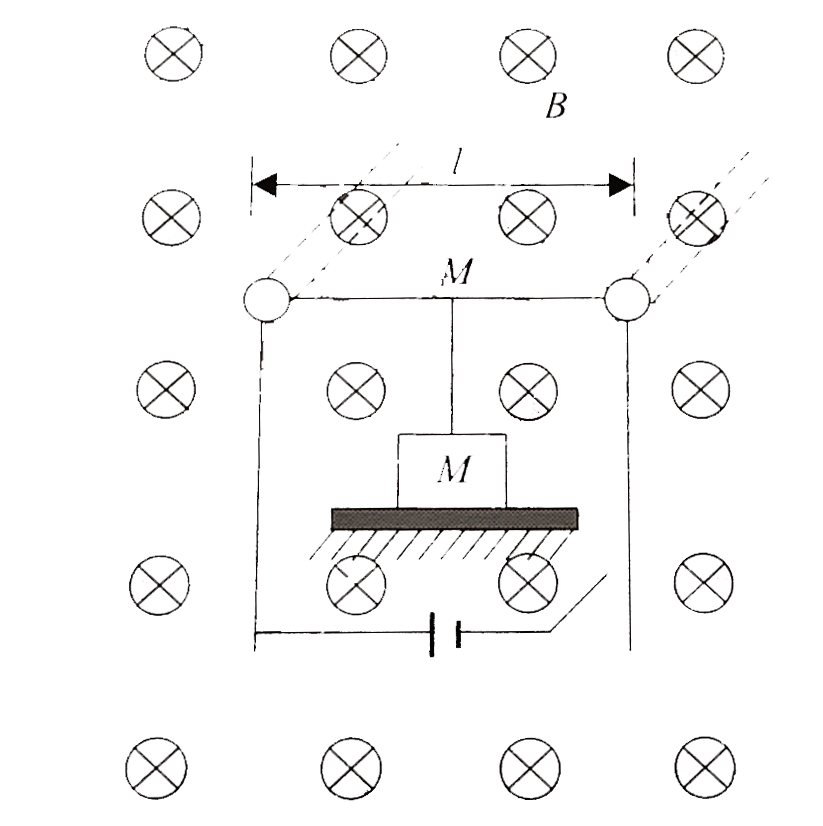
There exists a uniform magnetic field in horizontal direction perpendicular to the plane of the paper as shown in Fig. A wire of length 1 and mass m is attached with a block of equal mass with the help of an ideal string. The block is kept on floor and the wire on two conducting support as shown. After closing the switch, a charge q passes though the wire for a small interval of time. To what height the block will rise? (takeqBlm=20)
 View Solution
View SolutionQuestion 96
Figure shows a conducting frame having battery and a resistance on which a movable conductor of length 0.5 m can slide, The whole arrangement is placed in a uniform magnetic field of B =0.4 T directed perpendicular and into the plane of frame. Initially the circuit is open. When the key is inserted, the conductor begins to move. It is found that a force 0.5 N has to be applied on the conductor to the left to keep it moving at constant speed to the right.
Current flowing in the conductor is:
 View Solution
View SolutionQuestion 99
A conduting wire ABC (as shown) is moving with a constant velocity along horizontal direction. The magnetic field is perpendicular to the wire and directed into the page. AB =BC. Find the range of angle (θ) made by rod AB with horizontal at A so that value of induced emf at A is greater than at C
 View Solution
View SolutionQuestion 101
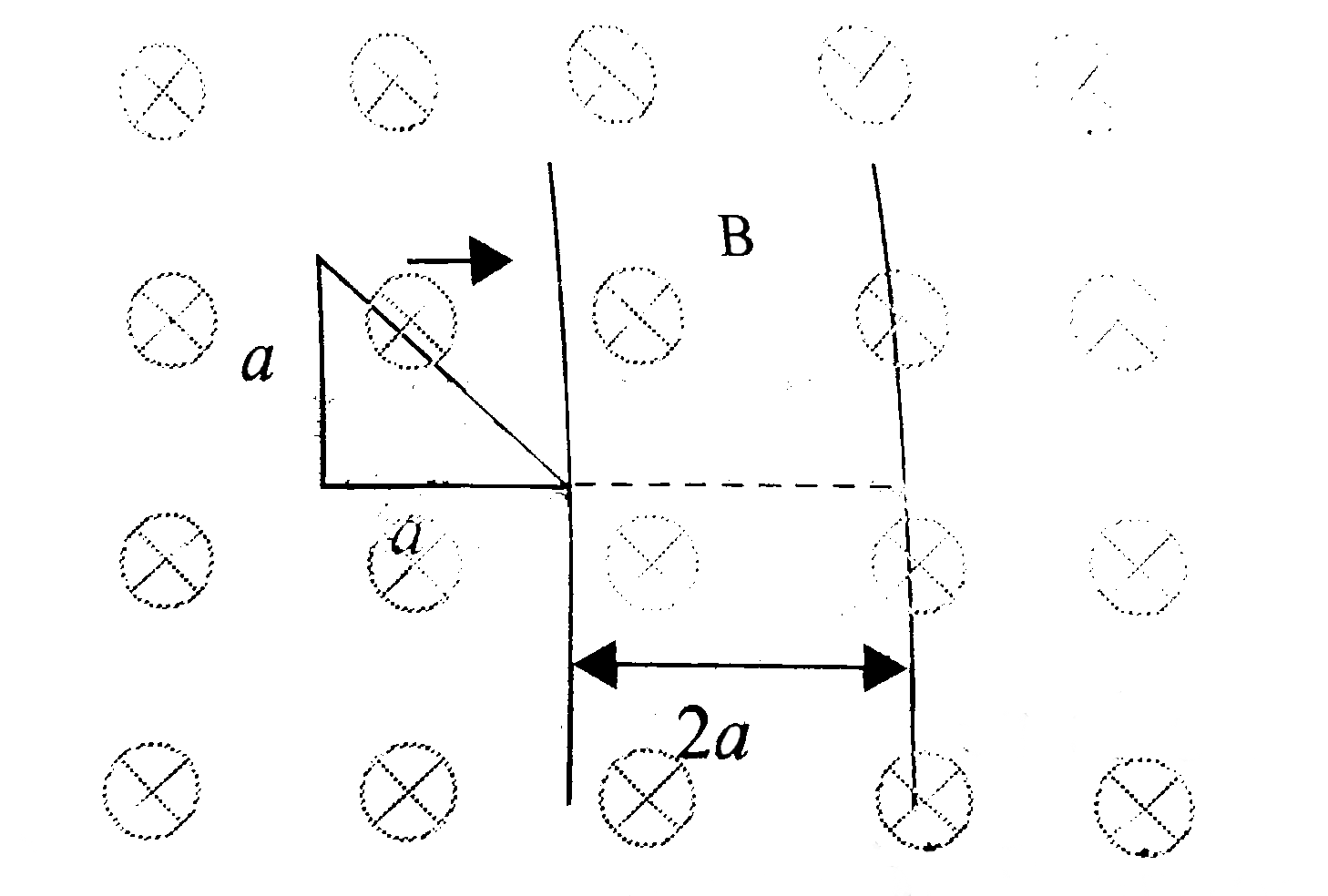
A right angled triangular loop as shown below enters uniform magnetic field (at right angle to the boundary of the field) directed into the paper. Draw the graph between induced emf e and the distance along the perpendicular to the boundary of the field, (say x) along which loop moves.
 View Solution
View SolutionQuestion 102
In a magnetic field as shown, in Fig. two horizontal wires of same mass and length l1andl2 are free to slide on different vertical rails with velocities v1andv2 respectively. If the resistance of two circuits are same and a1anda2 are acceleration of two horizontal wires respectively, the condition for a1>a2 is
 View Solution
View SolutionQuestion 103
In the previous problem, if two falling conductors attain velocities v1andv2 respectively after falling through same height h, ratio of energy dissipated as heat to the energy dissipated in resistor per unit time for two conductors is same.
Find which of the following condition will be satisfiedView SolutionQuestion 109
A plane rectangular loop is placed in a magnetic field. The emf induced in the loop due to this field is ε1 whose maximum value is εim. The loop was pulled out of the magnetic field at a variable velocity. Assume that →B is uniform and constant ε1 is plotted against t as shown in the graph.
Which of the following are/is correct statement(s):
 View Solution
View SolutionQuestion 134
Two straight conducting rails form a right angle where their ends are joined. A conducting bar in contact with the rails starts at the vertex at time t = 0 and moves with constant velocity v along them as shown in Fig. A magnetic field →B is directed into the page. the induced emf in the circuit at any time t is proportional to
 View Solution
View SolutionQuestion 141
A closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
A uniformly charged insulating ring is rotated in a uniform magnetic field about its own axis, thenView SolutionQuestion 142
A closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
Consider the situation shown in Fig., ring is having a uniformly distributed positive charge. Magnetic field is perpendicular to the axis of ring. Now ring is rotated in anticlockwise direction as seen from left hand side direction of magnetic torque acting on the ring is
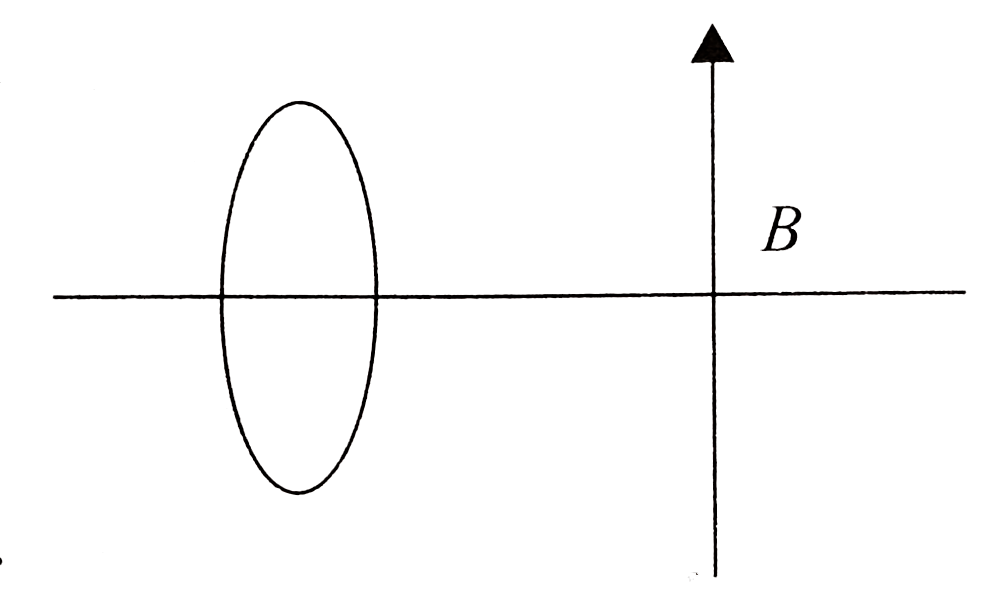 View Solution
View SolutionQuestion 143
A closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
Let ring in the above question is having a radius R and a charge Q is uniformly distributed over it. Ring is rotated with a constant angular velocity (ω) as mentioned above.
Torque acting on the ring due to magnetic force isView SolutionQuestion 144
A charged particle with charge to mass ratio (qm)=(10)319Ckg−1 enters a uniform magnetic field →B=20ˆi+30ˆj+50ˆkT at time t = 0 with velocity →V=(20ˆi+50ˆj+30ˆk)m/s. Assume that magnetic field exists in large space.
During the further motion of the particle in the magnetic field, the angle between the magnetic field and velocity of the particleView SolutionQuestion 145
A charged particle with charge to mass ratio (qm)=(10)319Ckg−1 enters a uniform magnetic field →B=20ˆi+30ˆj+50ˆkT at time t = 0 with velocity →V=(20ˆi+50ˆj+30ˆk)m/s. Assume that magnetic field exists in large space.
The frequency (in Hz) of the revolution of the particle in cycles per second will beView SolutionQuestion 146
A charged particle with charge to mass ratio (qm)=(10)319Ckg−1 enters a uniform magnetic field →B=20ˆi+30ˆj+50ˆkT at time t = 0 with velocity →V=(20ˆi+50ˆj+30ˆk)m/s. Assume that magnetic field exists in large space.
The pitch of the helical path of the motion of the particle will beView SolutionQuestion 147
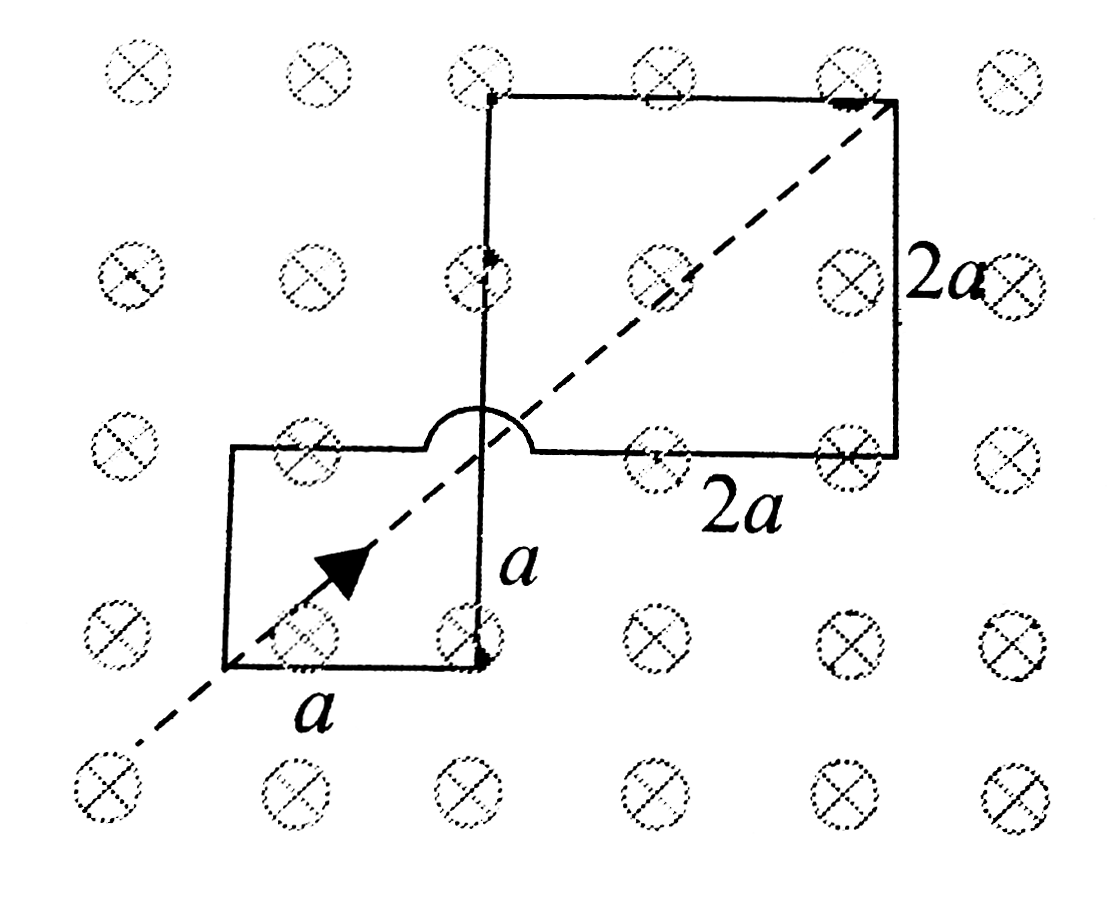
PQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=−9a/5, magnitude of induced current and its direction as seen from above will be: View SolutionQuestion 148
PQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

External force required to maintain constant velocity of the loop for x=−95a will beView SolutionQuestion 149
PQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=a/4
(i) magnetic flux through the loop,
(ii) induced current in the loop and
(iii) external force required to maintain constant velocity of the loop, will beView SolutionQuestion 150
An indcutor having self inductance L with its coil resistance R is connected across a battery of emf elipson. When the circuit is in steady state t = 0, an iron rod is inserted into the inductor due to which its inductance becomes nL (ngt1).
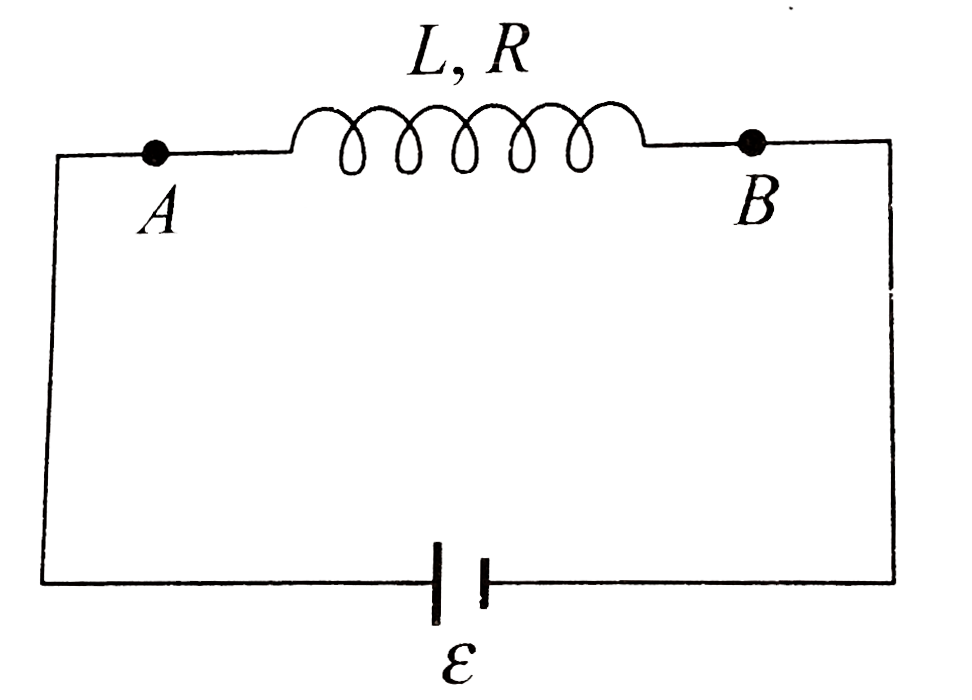
After insertion of rod which of the following quantities will change with time?
(1) Potential difference across terminals A and B
(2) Inductance
(3) Rate of heat produced in coilView SolutionQuestion 151
An indcutor having self inductance L with its coil resistance R is connected across a battery of emf elipson. When the circuit is in steady state t = 0, an iron rod is inserted into the inductor due to which its inductance becomes nL (ngt1).
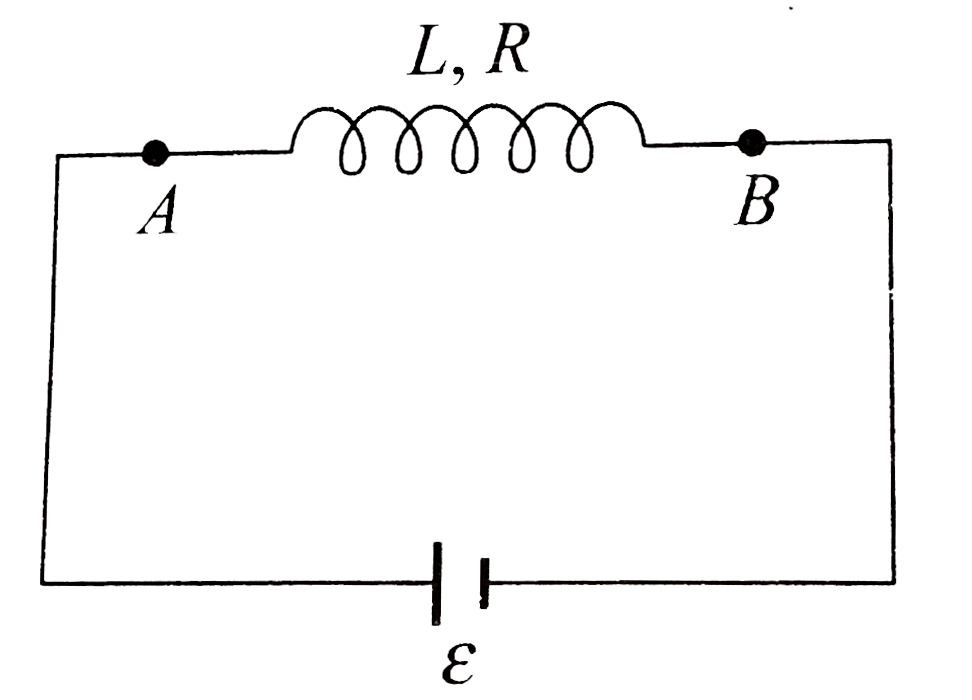
after insertion of rod, current in the circuit:View SolutionQuestion 152
An indcutor having self inductance L with its coil resistance R is connected across a battery of emf elipson. When the circuit is in steady state t = 0, an iron rod is inserted into the inductor due to which its inductance becomes nL (ngt1).

After insertion of rod which of the following quantities will change with time?
(1) Potential difference across terminals A and B
(2) Inductance
(3) Rate of heat produced in coilView SolutionQuestion 153
As a charged particle 'q' moving with a velocity →v enters a uniform magnetic field →B, it experience a force →F=q(→v×→B).Forθ=0∘or180∘,θ being the angle between →vand→B, force experienced is zero and the particle passes undeflected. For θ=90∘, the particle moves along a circular arc and the magnetic force (qvB) provides the necessary centripetal force (mv2/r). For other values of θ(θ≠0∘,180∘,90∘), the charged particle moves along a helical path which is the resultant motion of simultaneous circular and translational motions.
Suppose a particle that carries a charge of magnitude q and has a mass 4×10−15 kg is moving in a region containing a uniform magnetic field →B=−0.4ˆkT. At some instant, velocity of the particle is →v=(8ˆi−6ˆj4ˆk)×106ms−1 and force acting on it has a magnitude 1.6 N
Motion of charged particle will be along a helical path with View SolutionQuestion 154
As a charged particle 'q' moving with a velocity →v enters a uniform magnetic field →B, it experience a force →F=q(→v×→B).Forθ=0∘or180∘,θ being the angle between →vand→B, force experienced is zero and the particle passes undeflected. For θ=90∘, the particle moves along a circular arc and the magnetic force (qvB) provides the necessary centripetal force (mv2/r). For other values of θ(θ≠0∘,180∘,90∘), the charged particle moves along a helical path which is the resultant motion of simultaneous circular and translational motions.
Suppose a particle that carries a charge of magnitude q and has a mass 4×10−15 kg is moving in a region containing a uniform magnetic field →B=−0.4ˆkT. At some instant, velocity of the particle is →v=(8ˆi−6ˆj4ˆk)×106ms−1 and force acting on it has a magnitude 1.6 N
Angular frequency of rotation of particle, also called the cyclotron frequency' isView SolutionQuestion 155
As a charged particle 'q' moving with a velocity →v enters a uniform magnetic field →B, it experience a force →F=q(→v×→B).Forθ=0∘or180∘,θ being the angle between →vand→B, force experienced is zero and the particle passes undeflected. For θ=90∘, the particle moves along a circular arc and the magnetic force (qvB) provides the necessary centripetal force (mv2/r). For other values of θ(θ≠0∘,180∘,90∘), the charged particle moves along a helical path which is the resultant motion of simultaneous circular and translational motions.
Suppose a particle that carries a charge of magnitude q and has a mass 4×10−15 kg is moving in a region containing a uniform magnetic field →B=−0.4ˆkT. At some instant, velocity of the particle is →v=(8ˆi−6ˆj4ˆk)×106ms−1 and force acting on it has a magnitude 1.6 N
If the coordinates of the particle at t = 0 are (2 m, 1 m, 0), coordinates at a time t = 3 T, where T is the time period of circular component of motion. will be (take π=3.14)View SolutionQuestion 156
ABCDA is a closed loop of conducting wire consisting of two semicircular sections, the part ABCD lying in the XY plane and the part CDA lying in the YZ plane, both the parts having the centre at origin O (see the diagram). This loop is placed in a uniform field →B which varies with time.
Radius of the semicircular section is 0.5 m
If →B be directed along (+→i−→k) and decreases at the rate of 10−2Tesla/second, the magnitude and the sense of the induced emf in the loop, as seen along the magnetic field direction will beView SolutionQuestion 157
ABCDA is a closed loop of conducting wire consisting of two semicircular sections, the part ABCD lying in the XY plane and the part CDA lying in the YZ plane, both the parts having the centre at origin O (see the diagram). This loop is placed in a uniform field →B which varies with time.
Radius of the semicircular section is 0.5 m

If →B be directed along the vector (→i−→j) and decreases at the rate of 10−2Teslasecond. The magnitude and sense of the induced emf in the loop as seen along the positive x-axis will beView SolutionQuestion 158
ABCDA is a closed loop of conducting wire consisting of two semicircular sections, the part ABCD lying in the XY plane and the part CDA lying in the YZ plane, both the parts having the centre at origin O (see the diagram). This loop is placed in a uniform field →B which varies with time.
Radius of the semicircular section is 0.5 m
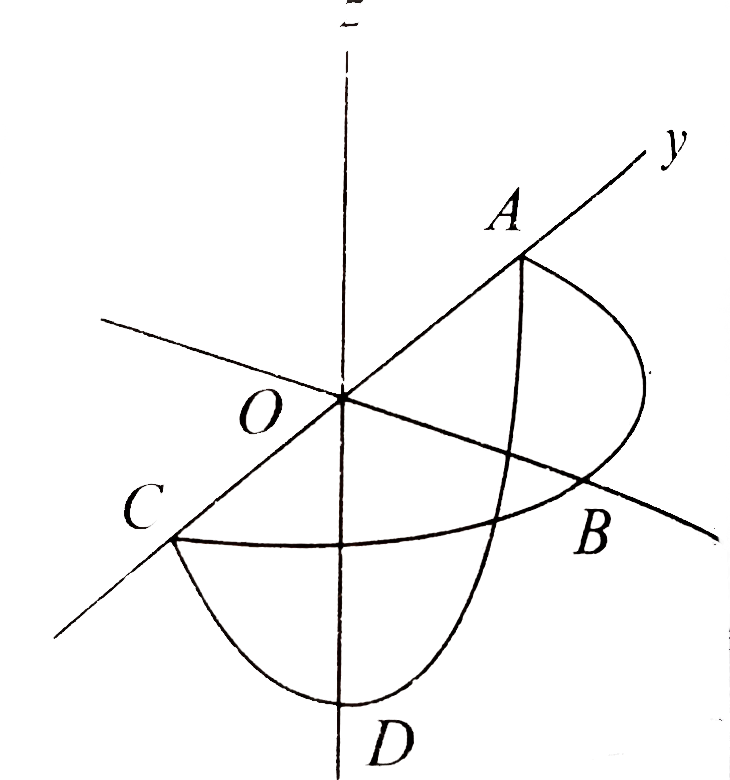
If →B be directed along the +z axis and increases at the rate of 10−2Teslasecond. the magnitude and sense of the induced emf in the loop as seen along the field direction will be View SolutionQuestion 159
A solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
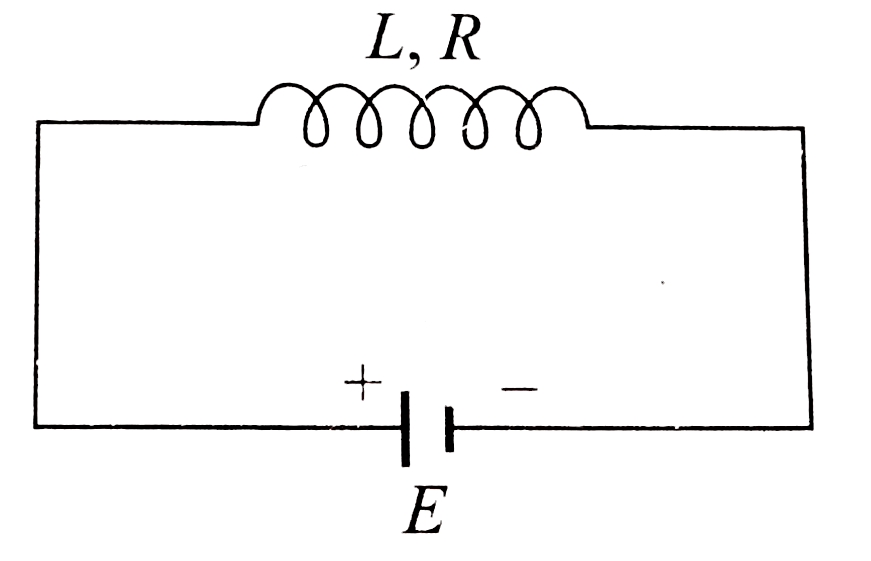
The work done to pull out the soft iron piece isView SolutionQuestion 160
A solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
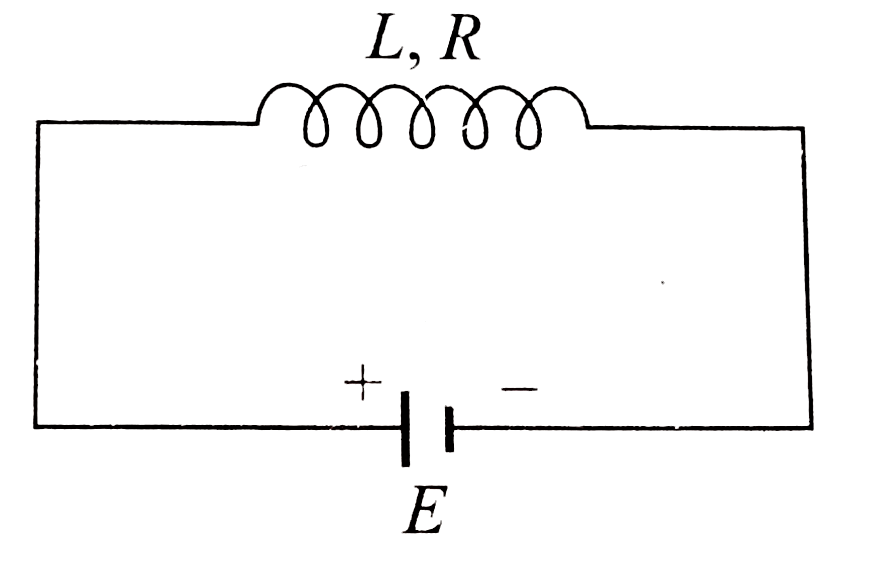
Assume t = 0 is the instant when iron piece has been pulled out, the current as a function of time after this is View SolutionQuestion 161
A solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
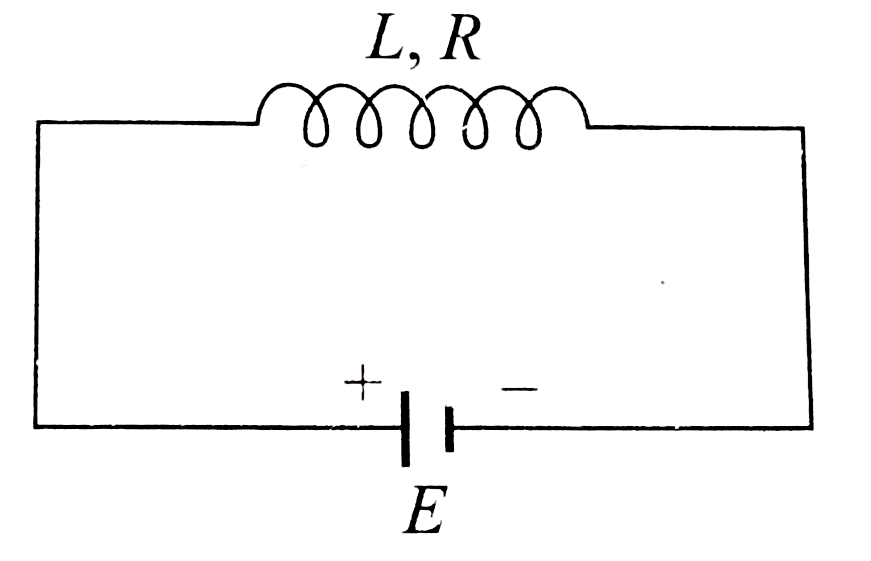
Power supplied by the battery as a function of timeView SolutionQuestion 162
The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
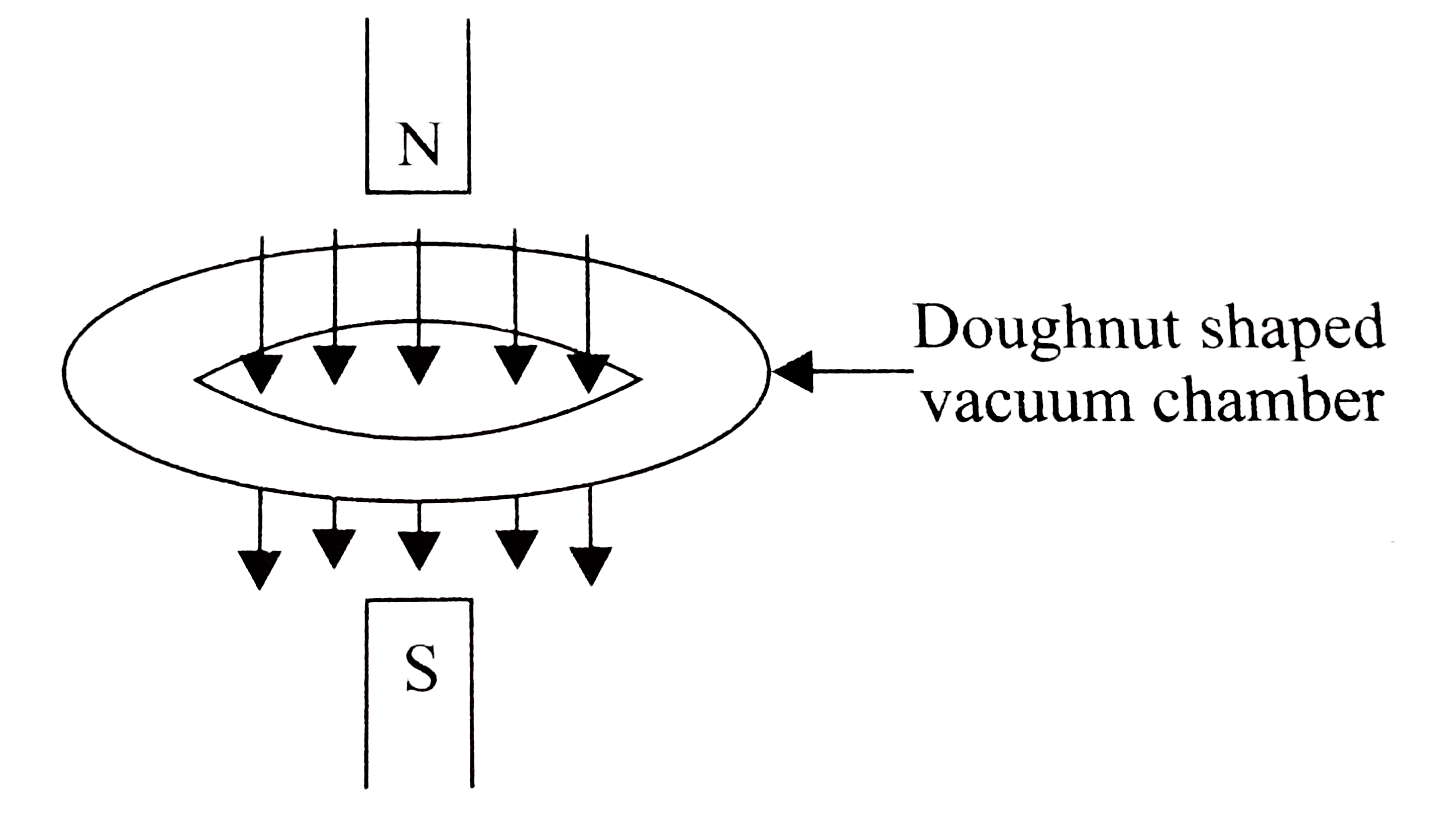
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Working of betatron is not based upon which of the following theories?View SolutionQuestion 163
The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.

An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Variable magnetic fluxView SolutionQuestion 164
The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
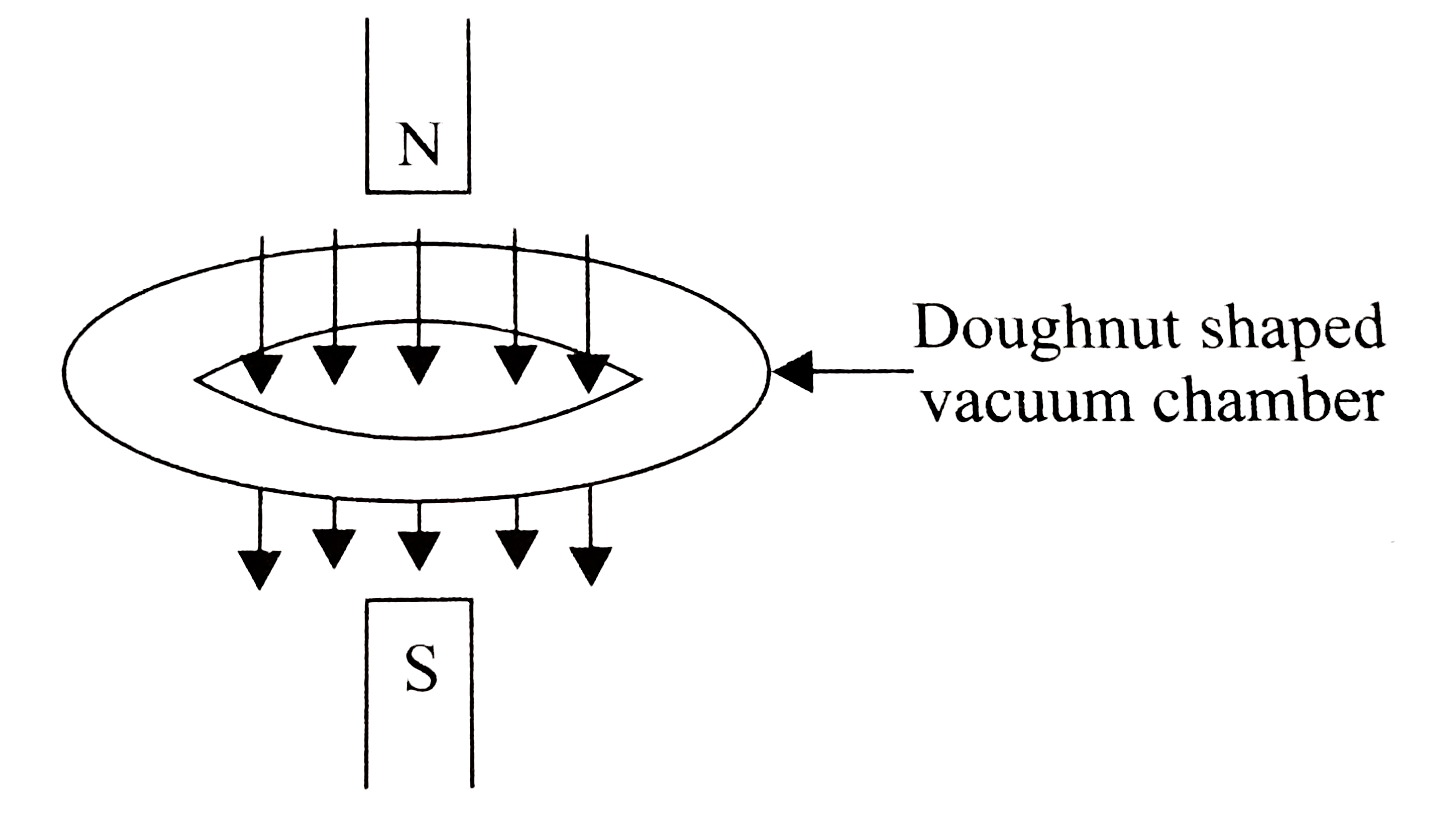
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Magnetic field which keeps the particles in circular path mustView SolutionQuestion 165
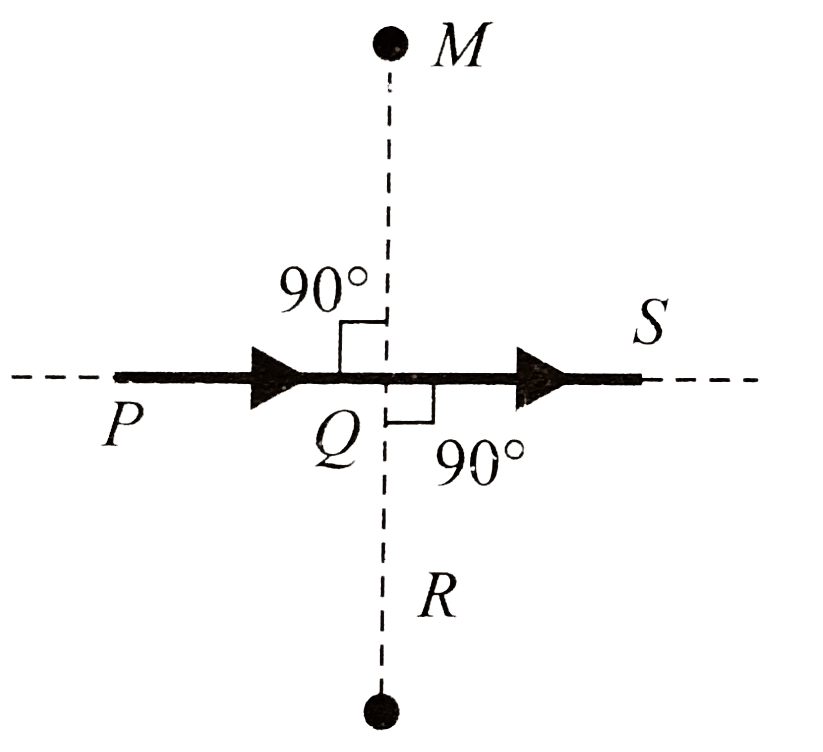
A velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
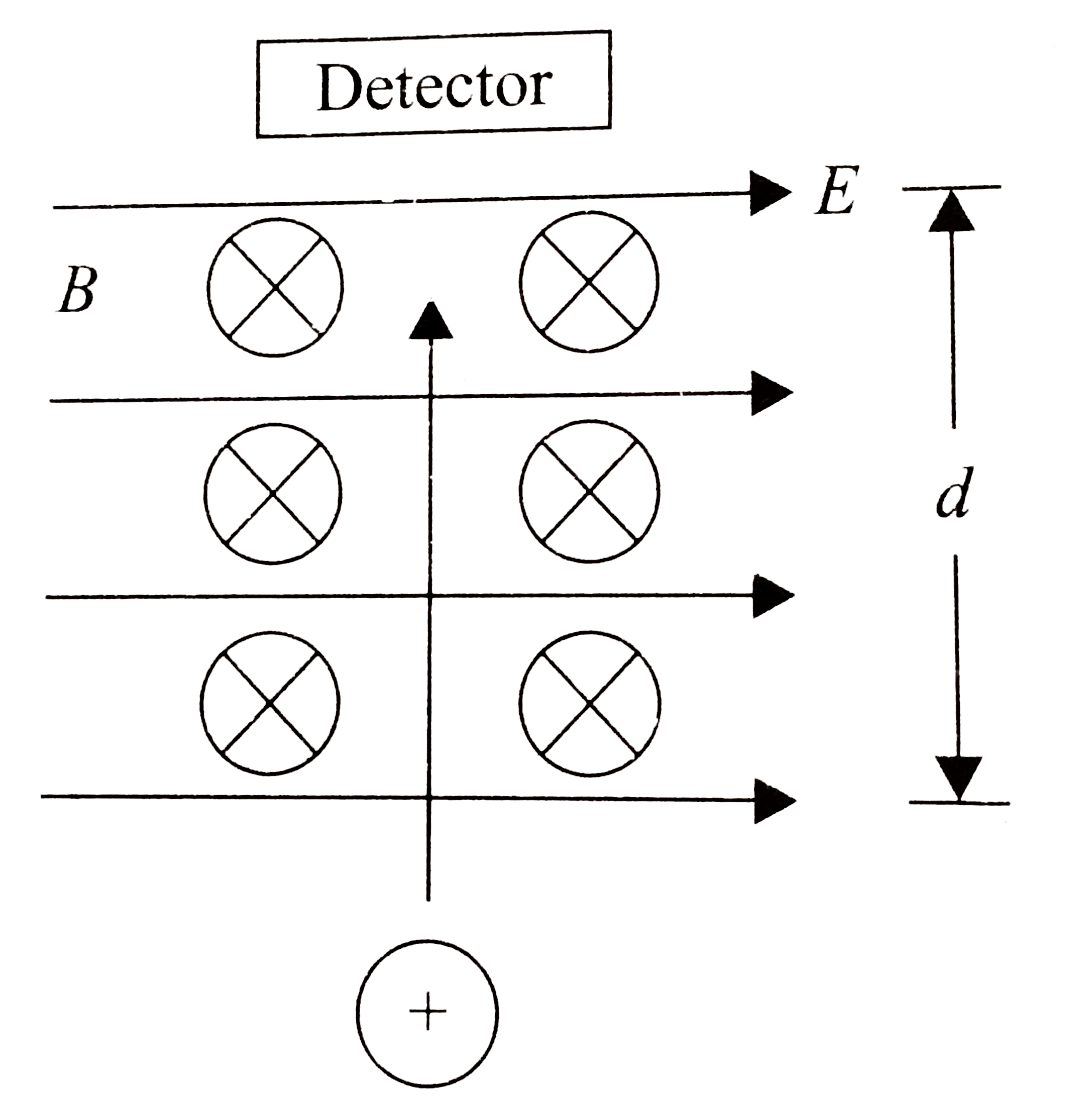
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?View SolutionQuestion 166
A velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.

The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?View SolutionQuestion 167
A velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
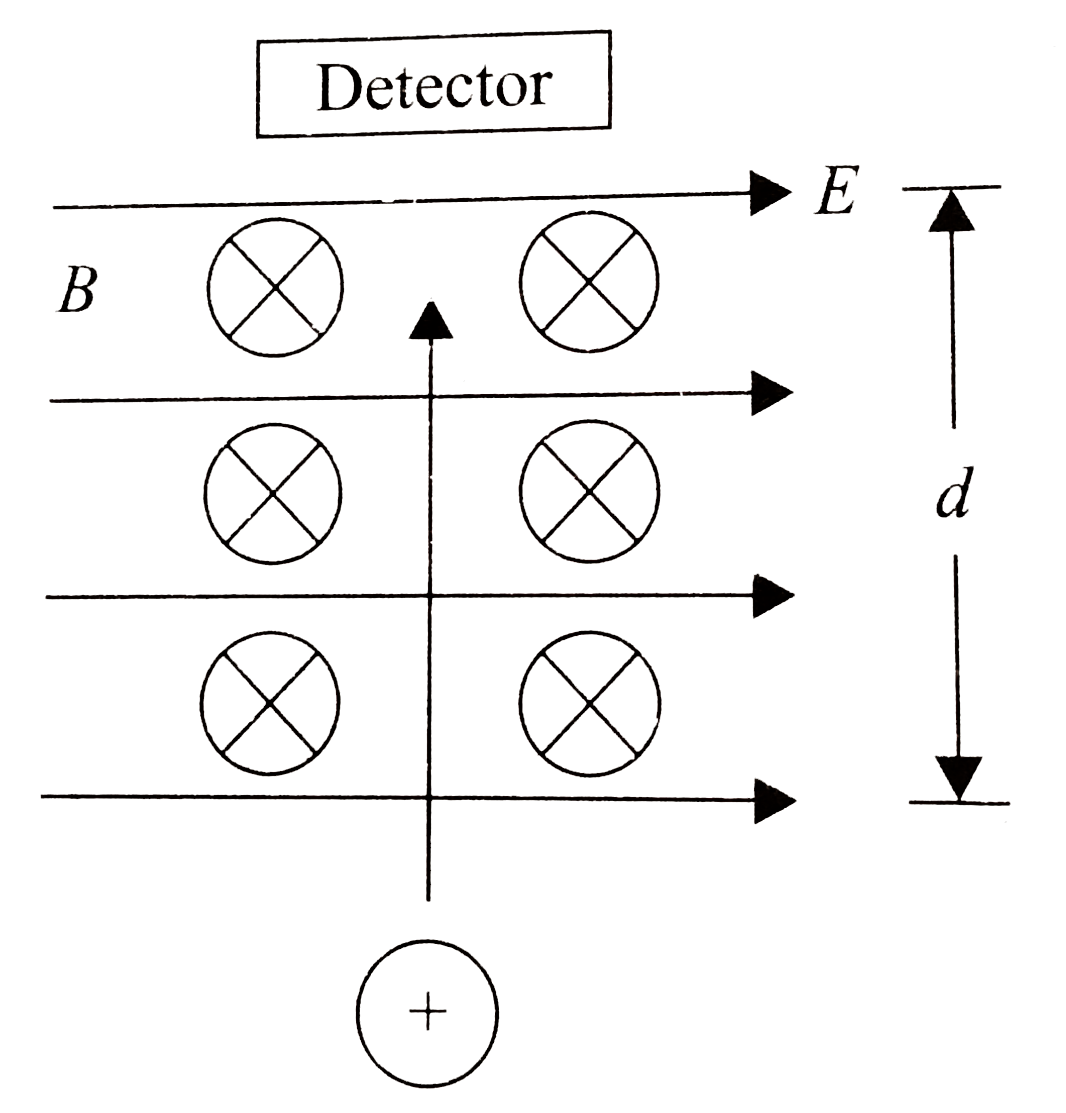
The moving particle will also experience a force due to magnetic field given by F = qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
If the filter is set to detect particles of speed v0, which one of the following diagrams best illustrates how the magnitude of the particle acceleration (a) depends on velocity v?View SolutionQuestion 168
In the given arrangement, the space between a pair of co-axial cylindrical conductors is evacuated. The outer cylinder, called anode, may be given a positive potential V relative to the inner cylinder.
A static homogeneous magnetic field →B parallel to the cylinder axis, directed out of plane of figure is aslo present. induced charges in the conductors are neglected.
We study the dynamics of electrons with rest mass m and charge e. The electrons are released at the surface of inner cylinder.
Consider the following two cases
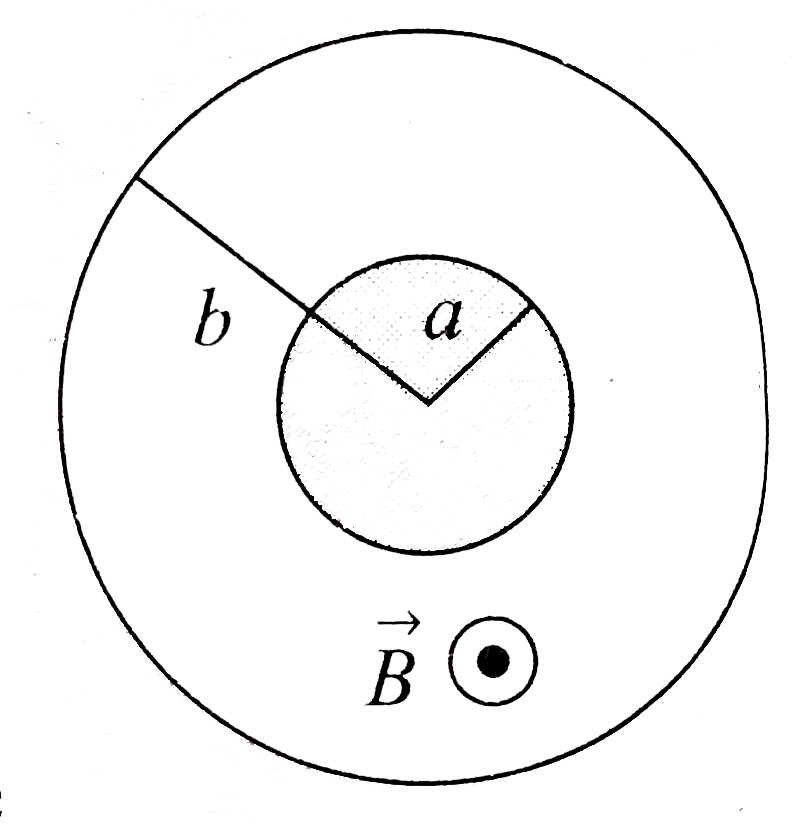
Case 1: Firstly the potential V is turned on, but →B=0. An electron with negligible velocity is ejected at the surface of inner cylinder. It is found to hit the anode.
Case 2: Now V = 0 but →B is present. An electron starts out with an initial velocity →v0 in radial direction. For magnetic field larger than critical value Bc the electron will not reach the anode.
Considering the case 1, the trajectory of electron will be View SolutionQuestion 169
In the given arrangement, the space between a pair of co-axial cylindrical conductors is evacuated. The outer cylinder, called anode, may be given a positive potential V relative to the inner cylinder.
A static homogeneous magnetic field →B parallel to the cylinder axis, directed out of plane of figure is aslo present. induced charges in the conductors are neglected.
We study the dynamics of electrons with rest mass m and charge e. The electrons are released at the surface of inner cylinder.
Consider the following two cases
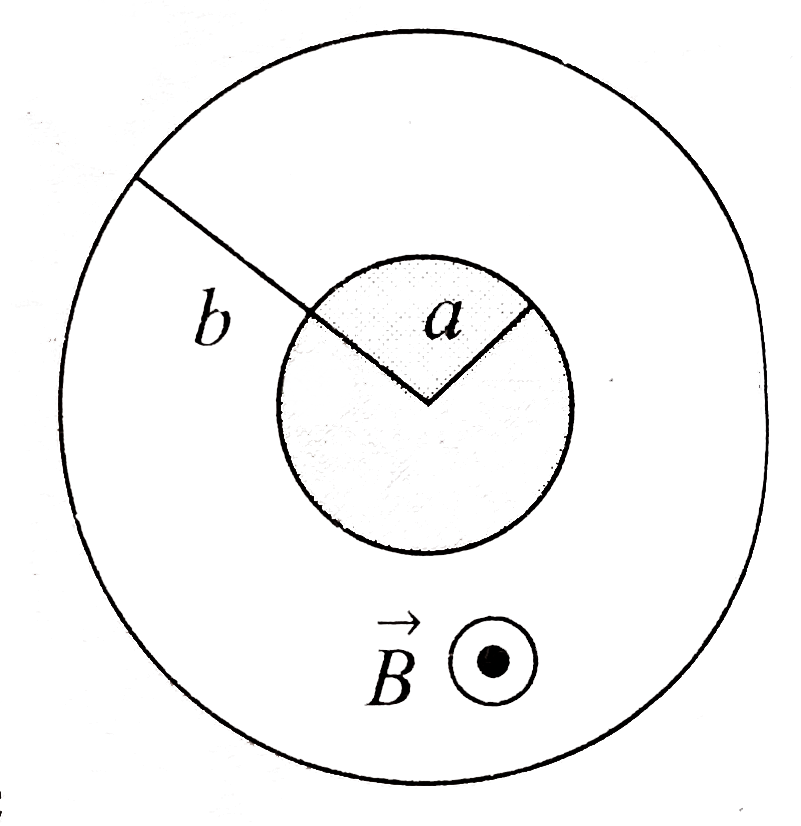
Case 1: Firstly the potential V is turned on, but →B=0. An electron with negligible velocity is ejected at the surface of inner cylinder. It is found to hit the anode.
Case 2: Now V = 0 but →B is present. An electron starts out with an initial velocity →v0 in radial direction. For magnetic field larger than critical value Bc the electron will not reach the anode.
Considering case 2, the trajectory of electron will beView SolutionQuestion 170
In the given arrangement, the space between a pair of co-axial cylindrical conductors is evacuated. The outer cylinder, called anode, may be given a positive potential V relative to the inner cylinder.
A static homogeneous magnetic field →B parallel to the cylinder axis, directed out of plane of figure is aslo present. induced charges in the conductors are neglected.
We study the dynamics of electrons with rest mass m and charge e. The electrons are released at the surface of inner cylinder.
Consider the following two cases
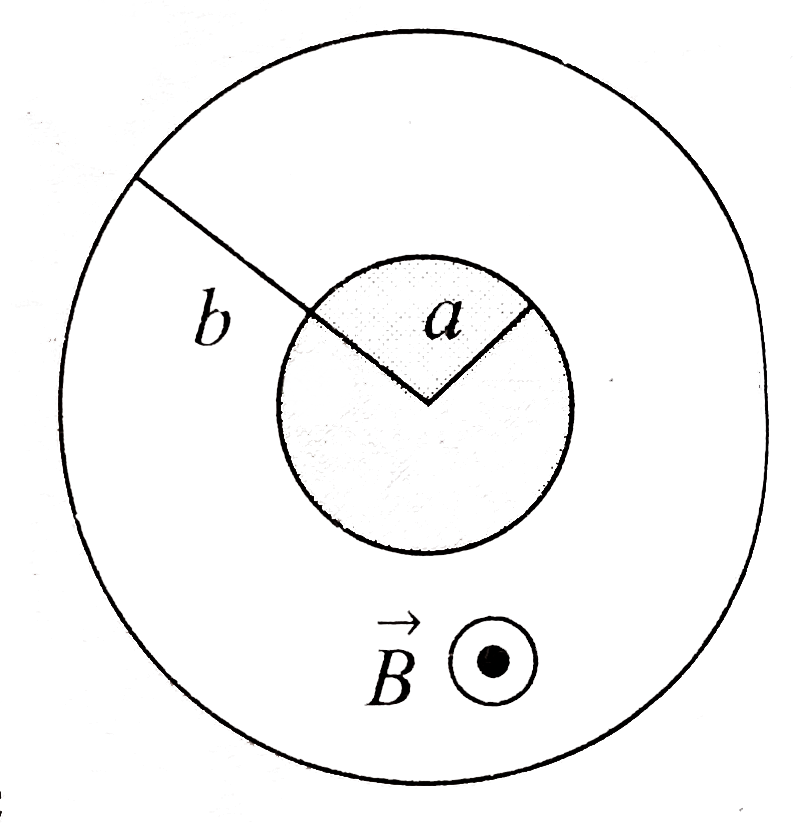
Case 1: Firstly the potential V is turned on, but →B=0. An electron with negligible velocity is ejected at the surface of inner cylinder. It is found to hit the anode.
Case 2: Now V = 0 but →B is present. An electron starts out with an initial velocity →v0 in radial direction. For magnetic field larger than critical value Bc the electron will not reach the anode.
The critical magnetic field Bc is given byView SolutionQuestion 171
The path of a charged particle in a uniform magnetic field depends on the angle θ between velocity vector and magnetic field, When θis0∘or180∘,Fm=0 hence path of a charged particle will be linear.
When θ=90∘, the magnetic force is perpendicular to velocity at every instant. Hence path is a circle of radius r=mvqB.
The time period for circular path will be T=2πmqB
When θ is other than 0∘,180∘and90∘, velocity can be resolved into two components, one along →B and perpendicular to B.
v|/|=cosθ
v^=vsinθ
The v⊥ component gives circular path and v|/| givestraingt line path. The resultant path is a helical path. The radius of helical path
r=mvsinθqB
ich of helix is defined as P=v|/|T
P=(2imvcosθ)
p=2πmvcosθqB
A charged particle moves in a uniform magnetic field. The velocity of particle at some instant makes acute angle with magnetic field. The path of the particle will be View SolutionQuestion 172
The path of a charged particle in a uniform magnetic field depends on the angle θ between velocity vector and magnetic field, When θis0∘or180∘,Fm=0 hence path of a charged particle will be linear.
When θ=90∘, the magnetic force is perpendicular to velocity at every instant. Hence path is a circle of radius r=mvqB.
The time period for circular path will be T=2πmqB
When θ is other than 0∘,180∘and90∘, velocity can be resolved into two components, one along →B and perpendicular to B.
v|/|=cosθ
v^=vsinθ
The v⊥ component gives circular path and v|/| givestraingt line path. The resultant path is a helical path. The radius of helical path
r=mvsinθqB
ich of helix is defined as P=v|/|T
P=(2imvcosθ)
p=2πmvcosθqB
Two ions having masses in the ratio 1:1 and charges 1:2 are projected from same point into a uniform magnetic field with speed in the ratio 2:3 perpendicular to field. The ratio of radii of circle along which the two particles move is : View SolutionQuestion 173
The path of a charged particle in a uniform magnetic field depends on the angle θ between velocity vector and magnetic field, When θis0∘or180∘,Fm=0 hence path of a charged particle will be linear.
When θ=90∘, the magnetic force is perpendicular to velocity at every instant. Hence path is a circle of radius r=mvqB.
The time period for circular path will be T=2πmqB
When θ is other than 0∘,180∘and90∘, velocity can be resolved into two components, one along →B and perpendicular to B.
v|/|=cosθ
v^=vsinθ
The v⊥ component gives circular path and v|/| givestraingt line path. The resultant path is a helical path. The radius of helical path
r=mvsinθqB
ich of helix is defined as P=v|/|T
P=(2imvcosθ)
p=2πmvcosθqB
Which particle will have minimum frequency of revolution when projected with the same velocity perpendicular to a magnetic field. View SolutionQuestion 174
Magnetic force on a charged particle is given by →Fm=q(→v×→B) and electrostatic force →Fe=q→E. A particle having charge q = 1C and mass 1 kg is released from rest at origin. There are electric and magnetic field given by →E=(10ˆi)N/Cforx=1.8m and →B=−(5ˆk)T for 1.8m≤x≤2.4m
A screen is placed parallel to y-z plane at x=3m. Neglect gravity forces.
The speed with which the particle will collide the screen is View SolutionQuestion 175
A particle having charge q=1 C and mass m=1kg is released from rest at origin. There are electric and manetic fields given by
E=(10ˆi)N/Cforx≤1.8m and
B=(−5ˆK)Tfor1.8m≤x≤2.4m A screen is placed parallel to y-z palane at x=3.0m. Neglect gravity forces.
y-coordinate of particle where it collides with be screen is .....m.View SolutionQuestion 176
Magnetic force on a charged particle is given by →Fm=q(→v×→B) and electrostatic force →Fe=q→E. A particle having charge q = 1C and mass 1 kg is released from rest at origin. There are electric and magnetic field given by →E=(10ˆi)N/Cforx=1.8m and →B=−(5ˆk)T for 1.8m≤x≤2.4m
A screen is placed parallel to y-z plane at x=3m. Neglect gravity forces.
The speed with which the particle will collide the screen is View SolutionQuestion 177
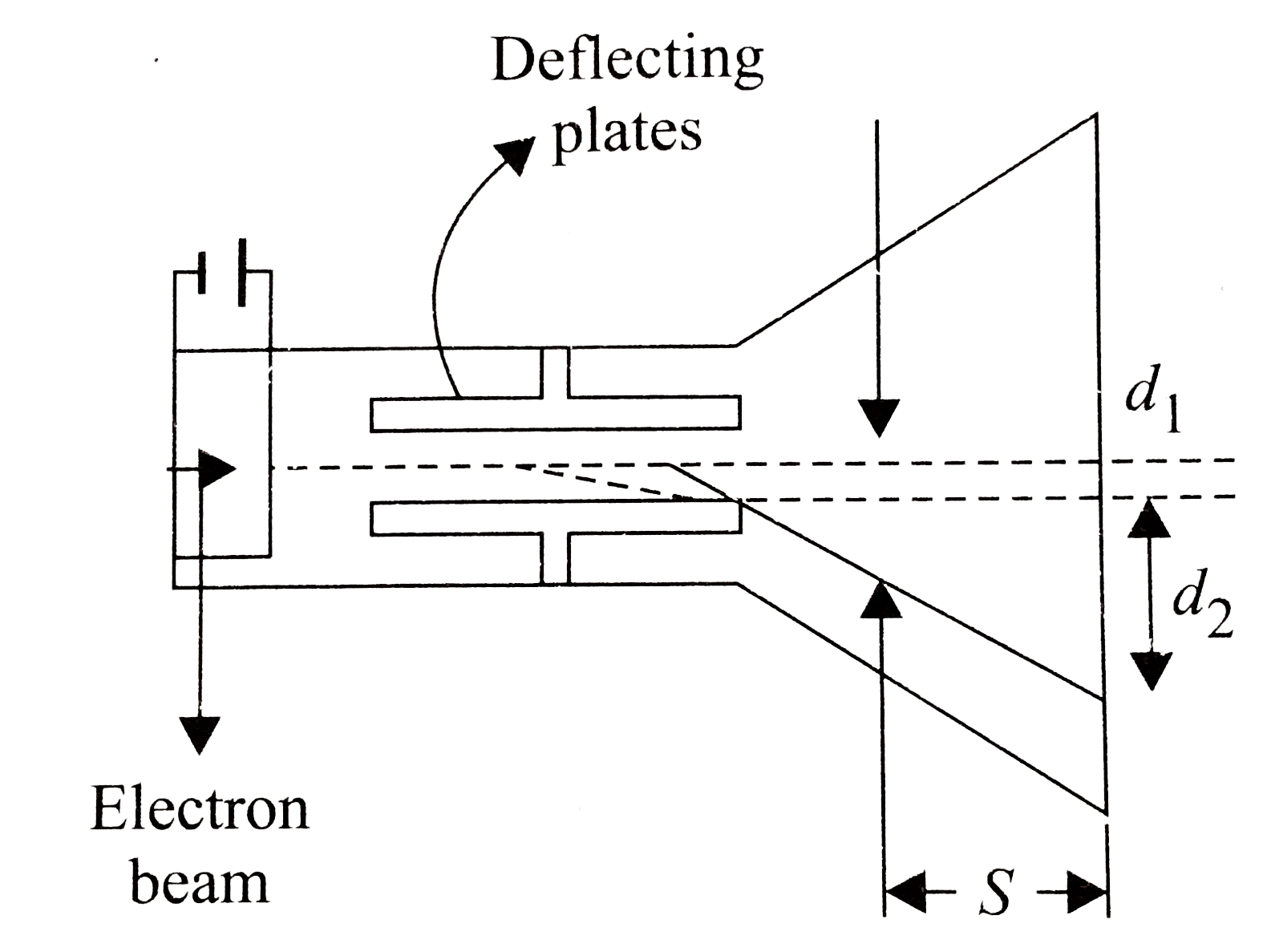
Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
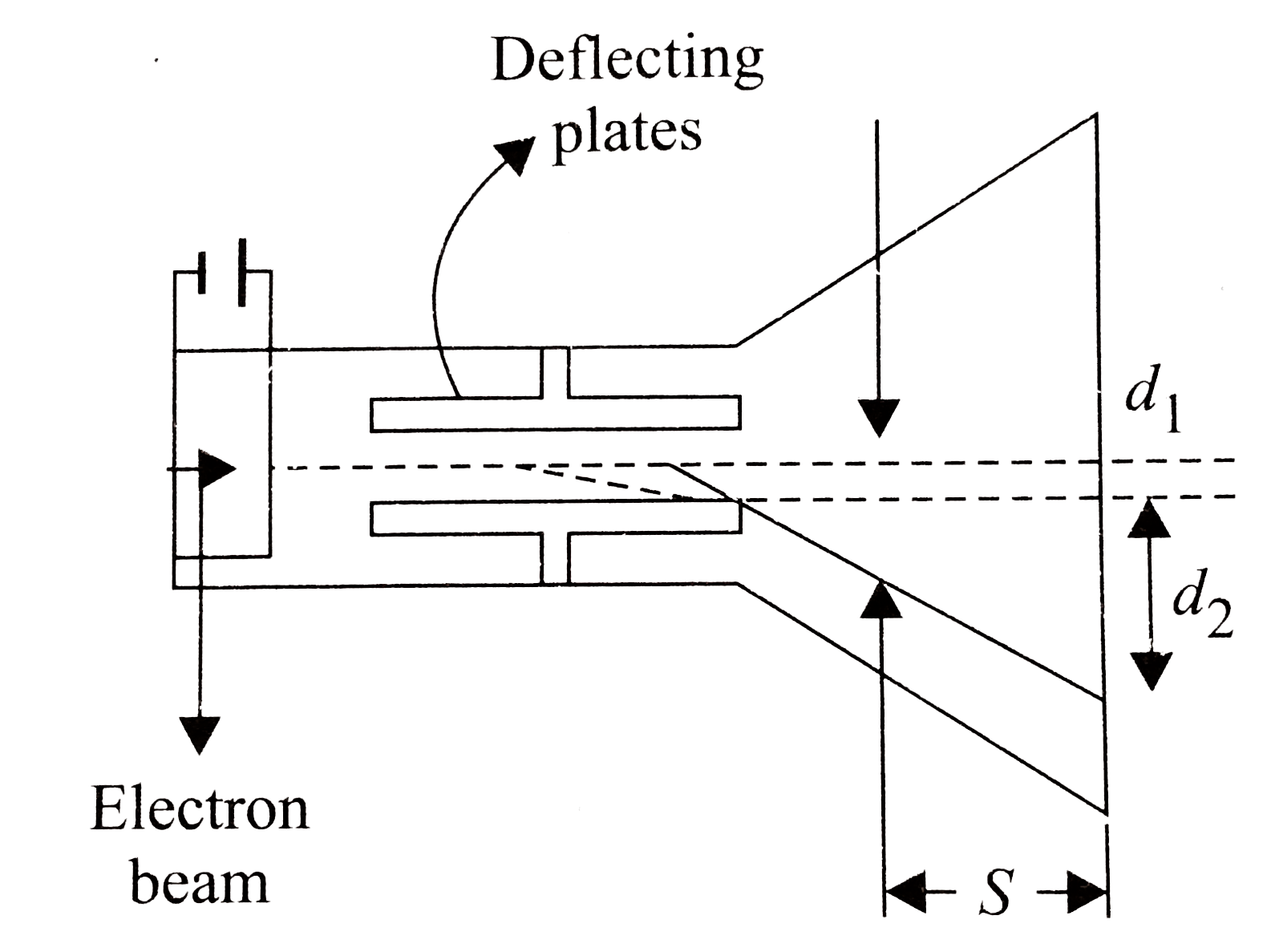
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experimentView SolutionQuestion 178
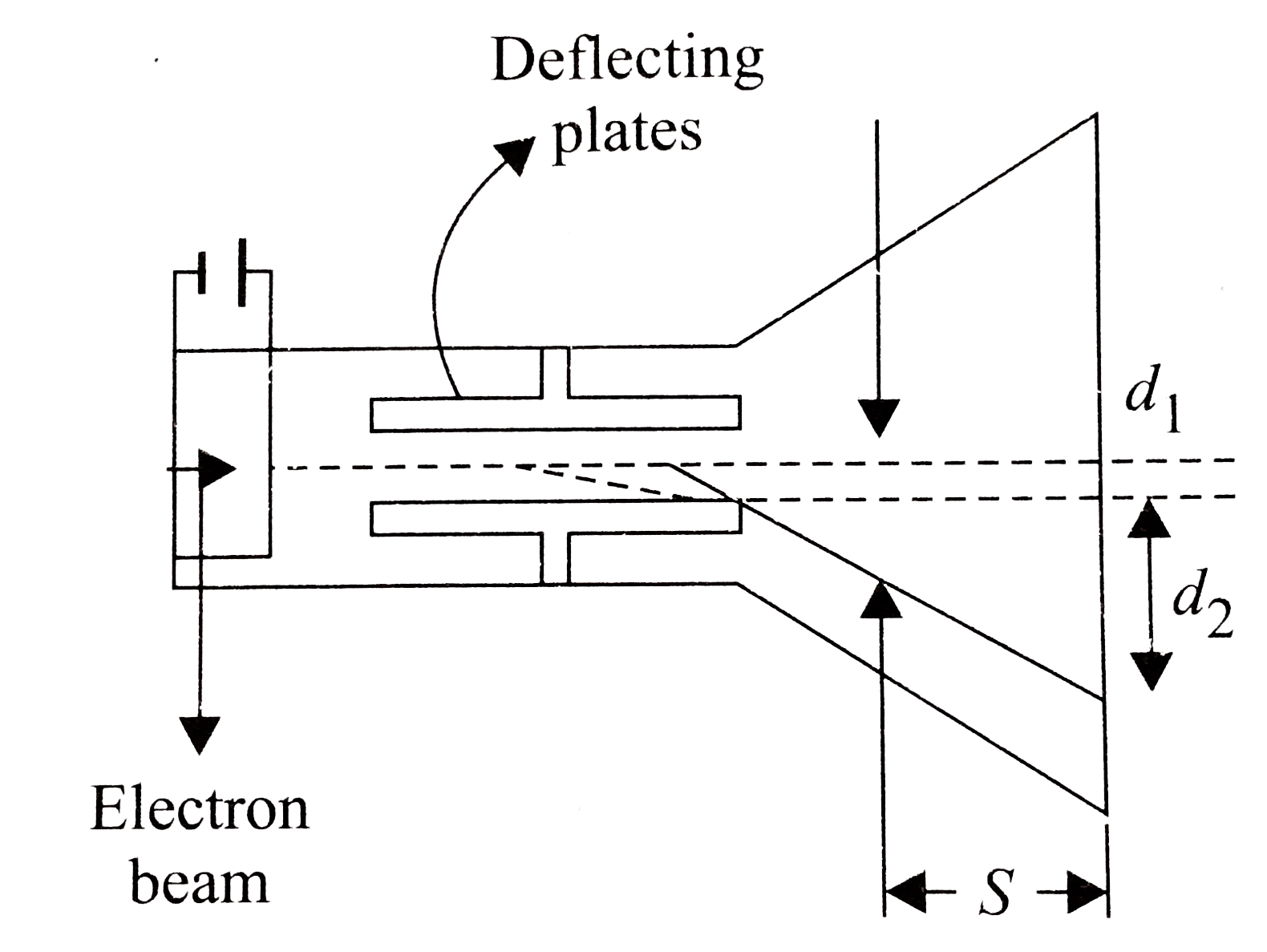
Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron is View SolutionQuestion 179
Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron speed were doubled by increasing the potential differece V, which of the following would be true in order to correctly measure e/mView SolutionQuestion 180
In uniform magnetic field, if angle between →vand→Bis0∘<0<90∘, the path of particle is helix. Let v1 be the component of →valong→Bandv2 be the component perpendicular to →B. Suppose p is the pitch. T is the time period and r is the radius of helix. Then
T=2πmqB,r=mv2qB,P=(v1)T
Assume a charged particle of charge q and mass m is released from the origin with velocity →v=v0ˆi−v0ˆk in a uniform magnetic field →B=−B0ˆk.
Pitch of helical path described by particle isView SolutionQuestion 181
In uniform magnetic field, if angle between →vand→Bis0∘<0<90∘, the path of particle is helix. Let v1 be the component of →valong→Bandv2 be the component perpendicular to →B. Suppose p is the pitch. T is the time period and r is the radius of helix. Then
T=2πmqB,r=mv2qB,P=(v1)T
Assume a charged particle of charge q and mass m is released from the origin with velocity →v=v0ˆi−v0ˆk in a uniform magnetic field →B=−B0ˆk.
Angle between v and B is View SolutionQuestion 182
In uniform magnetic field, if angle between →vand→Bis0∘<0<90∘, the path of particle is helix. Let v1 be the component of →valong→Bandv2 be the component perpendicular to →B. Suppose p is the pitch. T is the time period and r is the radius of helix. Then
T=2πmqB,r=mv2qB,P=(v1)T
Assume a charged particle of charge q and mass m is released from the origin with velocity →v=v0ˆi−v0ˆk in a uniform magnetic field →B=−B0ˆk.
Axis of helix is alongView SolutionQuestion 183
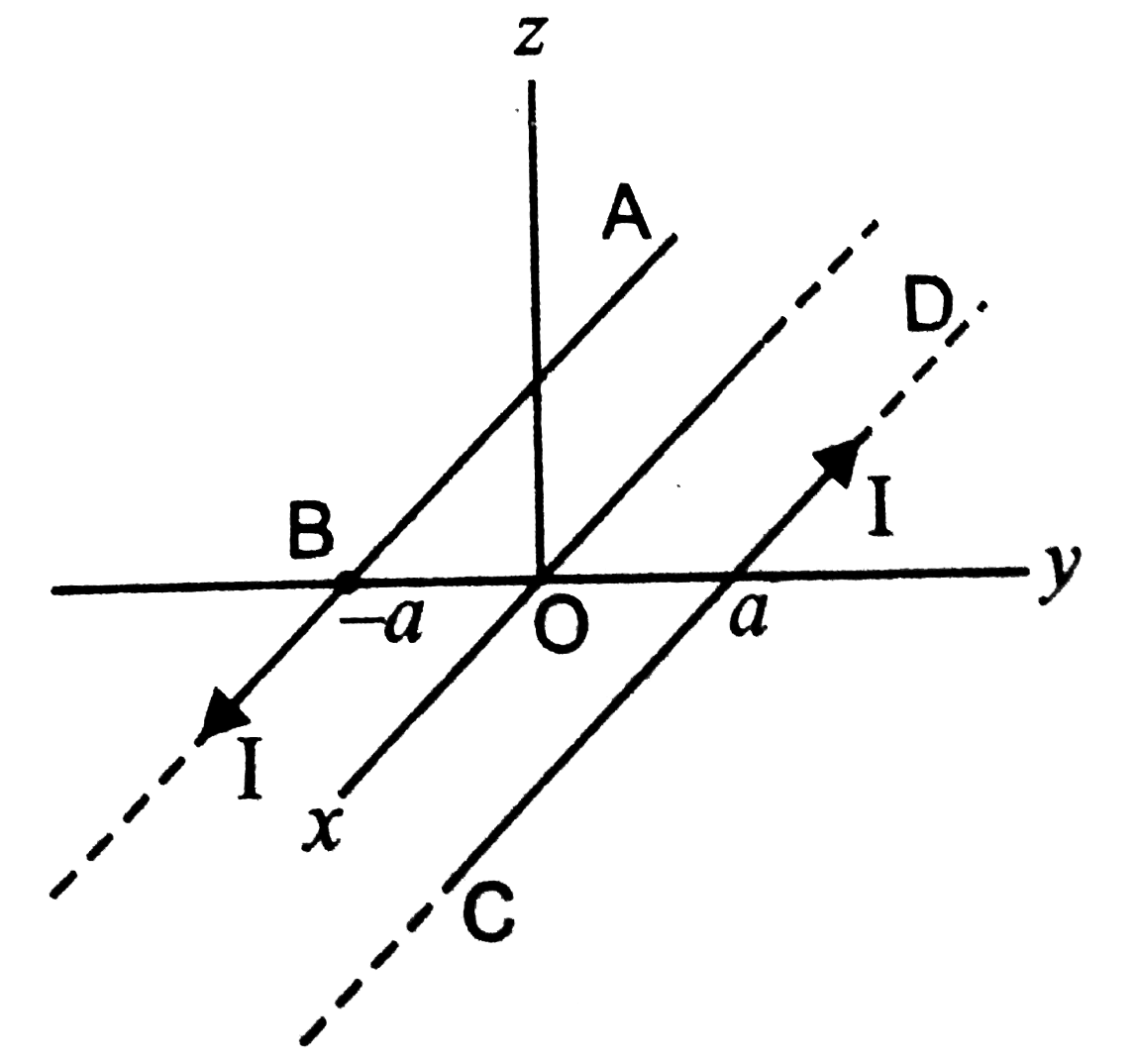
A straight segment OC(of length L meter) of a circuit carrying a current Iamp is placed along the x- axis ( fig.). Two infinetely long straight wires AandB , each extending from z=−∞→+∞, are fixed at y = -a meter and y = +a meter respectively, as shown in the figure.
If the wires AandB each carry a current Iamp into the plane of the paper, obtain the expression for the force acting on the segment OC. What will be the force on OC if the current in the wire B is reversed?
 View Solution
View SolutionQuestion 184
A straight segment OC(of length L meter) of a circuit carrying a current Iamp is placed along the x- axis ( fig.). Two infinetely long straight wires AandB , each extending from z=−∞→+∞, are fixed at y = -a meter and y = +a meter respectively, as shown in the figure.
If the wires AandB each carry a current Iamp into the plane of the paper, obtain the expression for the force acting on the segment OC. What will be the force on OC if the current in the wire B is reversed?
 View Solution
View SolutionQuestion 193
A square wire loop with 2 m sides is perpendicular to a uniform magnetic field, with half the area of the loop in the field (see Fig.) The loop contains a 20 V battery with negligible internal resistance. If the magnitude of the field varies with time according to B=(2+5t), with B in tesla and t in second.
What is the total emf in the circuit ?View SolutionQuestion 194
A square wire loop with 2 m sides is perpendicular to a uniform magnetic field, with half the area of the loop in the field (see Fig.) The loop contains a 20 V battery with negligible internal resistance. If the magnitude of the field varies with time according to B = (2 + 5t), with B in tesla and t in second.
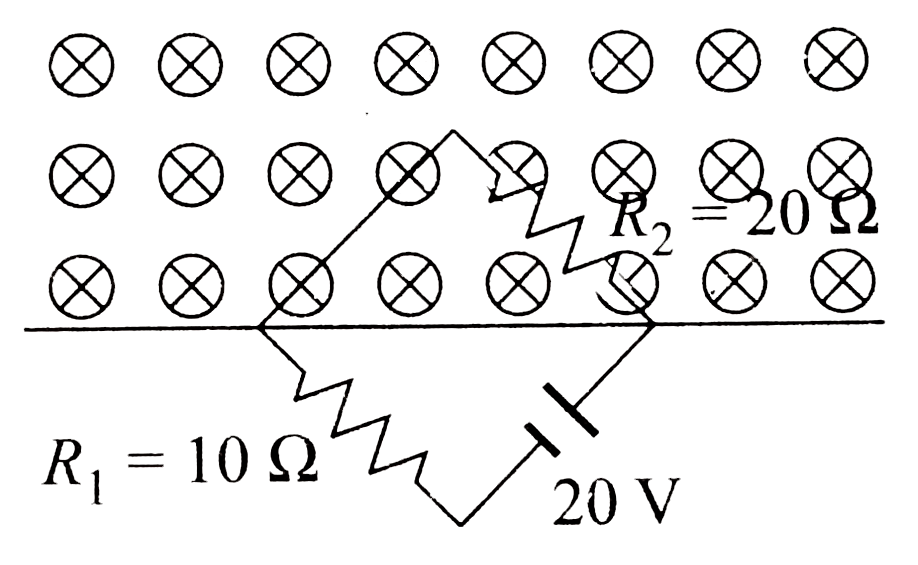
What is the current through the battery ?View SolutionQuestion 195
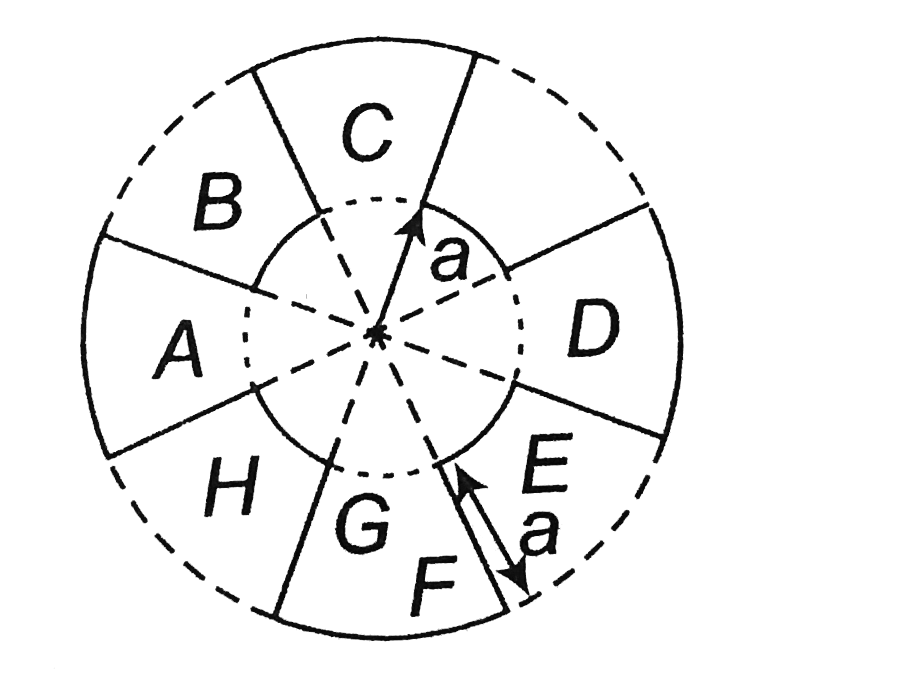
In a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At t=0 the rod was situated along the +X direction.
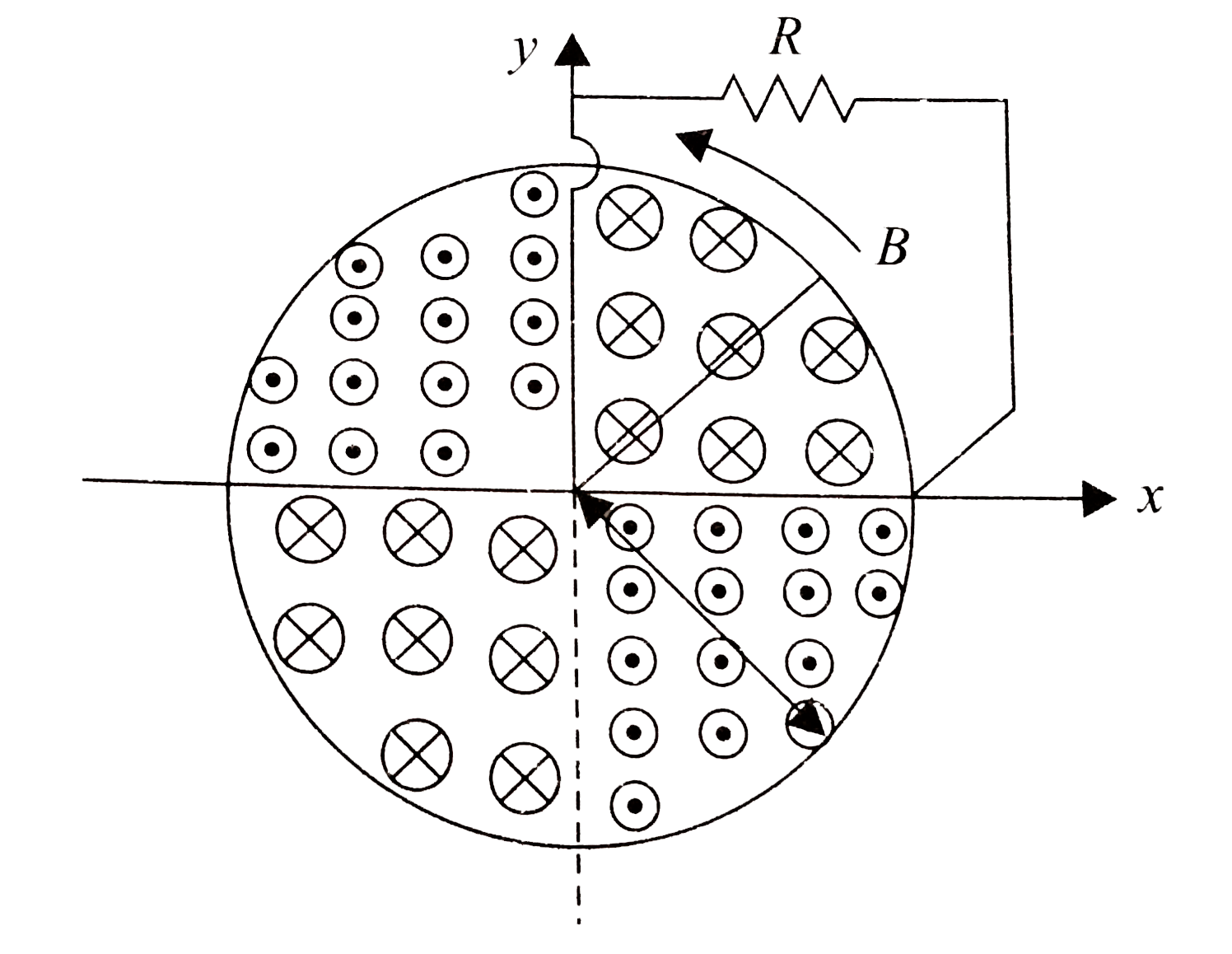
Find and plot the time dependence of the current in the resistance R when rod rotates with a constant angular velocity (ω).View SolutionQuestion 196
In a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At t = 0 the rod was situated along the +X direction.
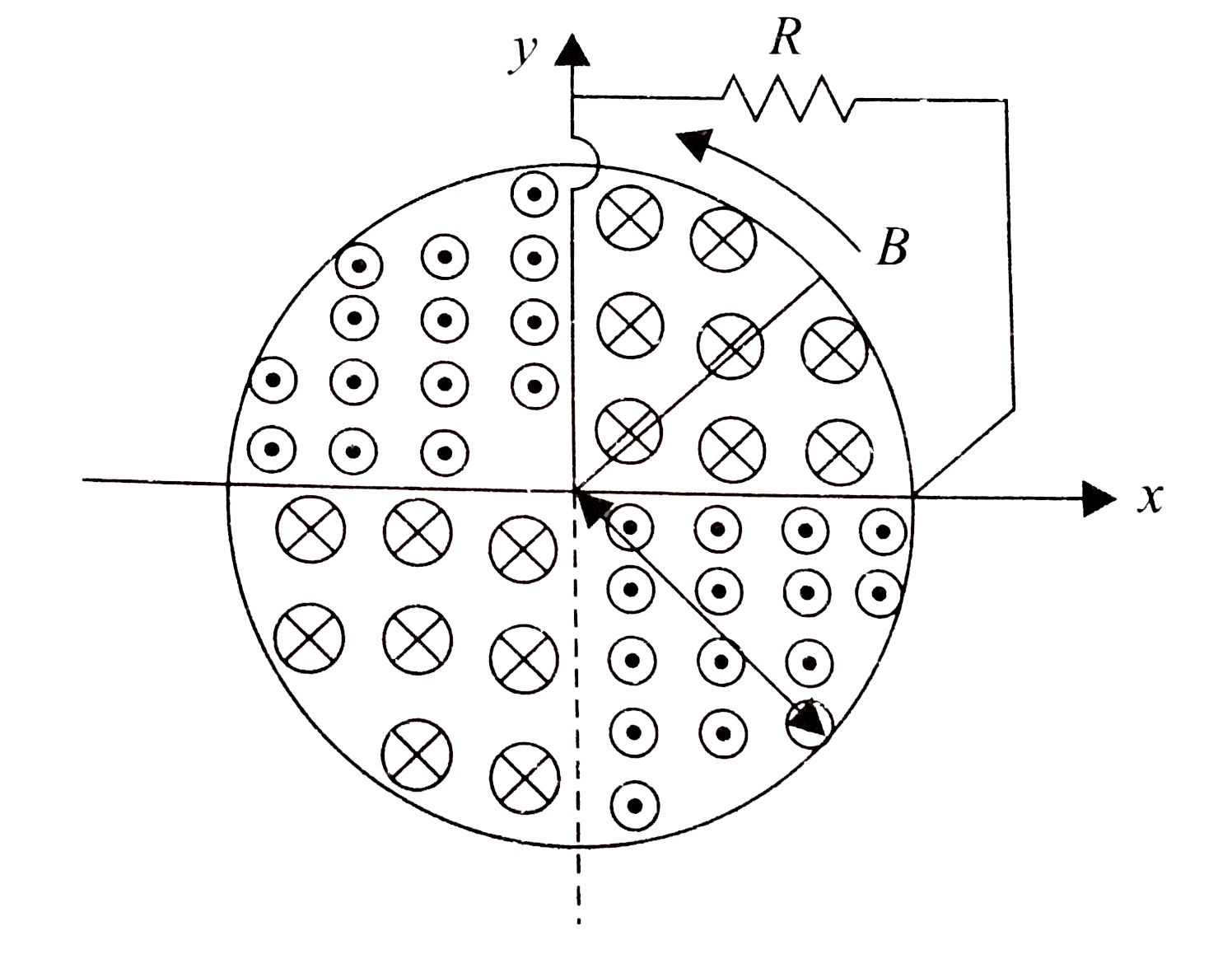
Find and plot the time dependence of the current in the resistance R when rotates with a constant angular acceleration (α)View SolutionQuestion 197
In a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At t = 0 the rod was situated along the +X direction.
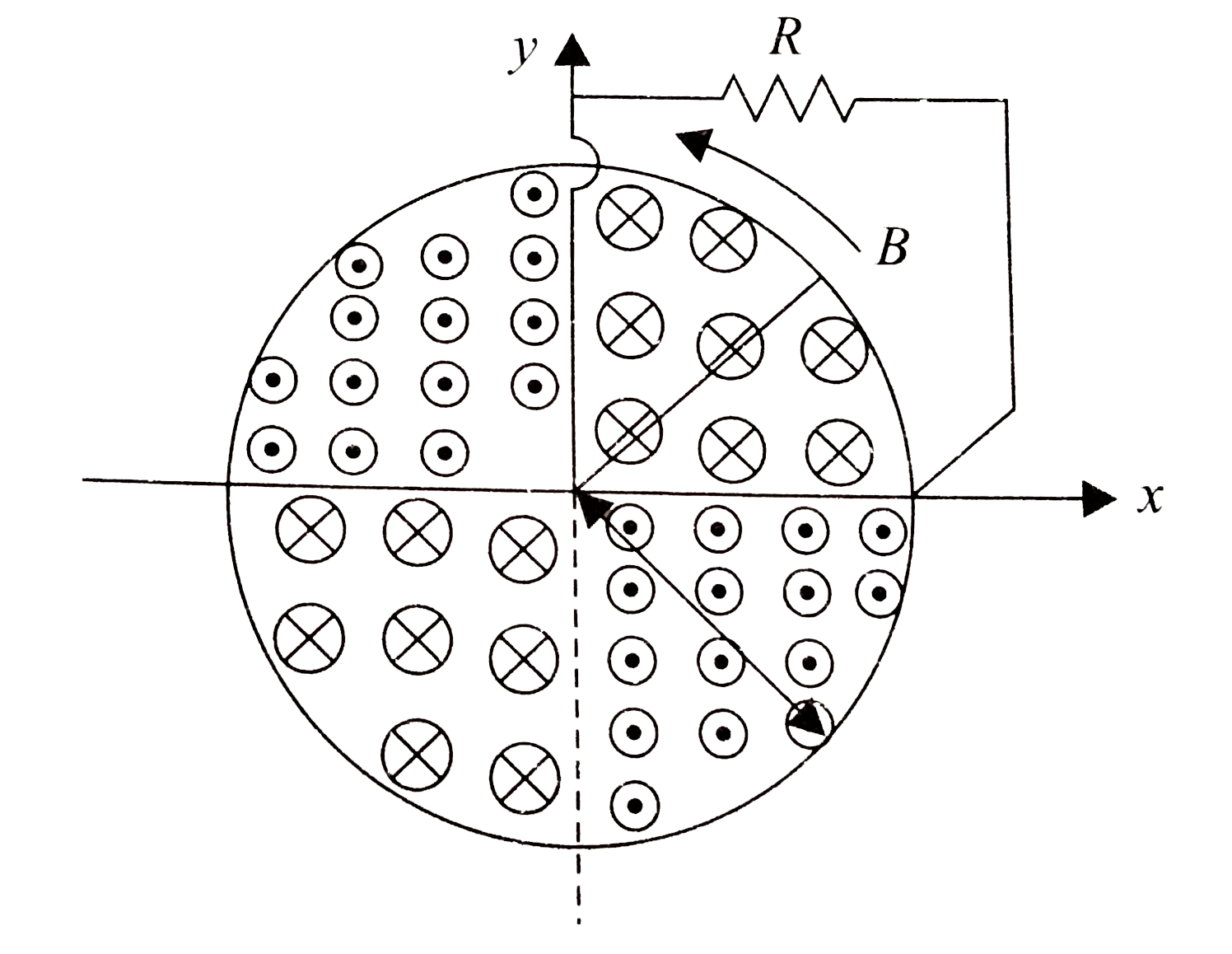
Find and plot the time dependence of the thermal power in the resistance R when rod rotates with a constant angular acceleration (α)View SolutionQuestion 199
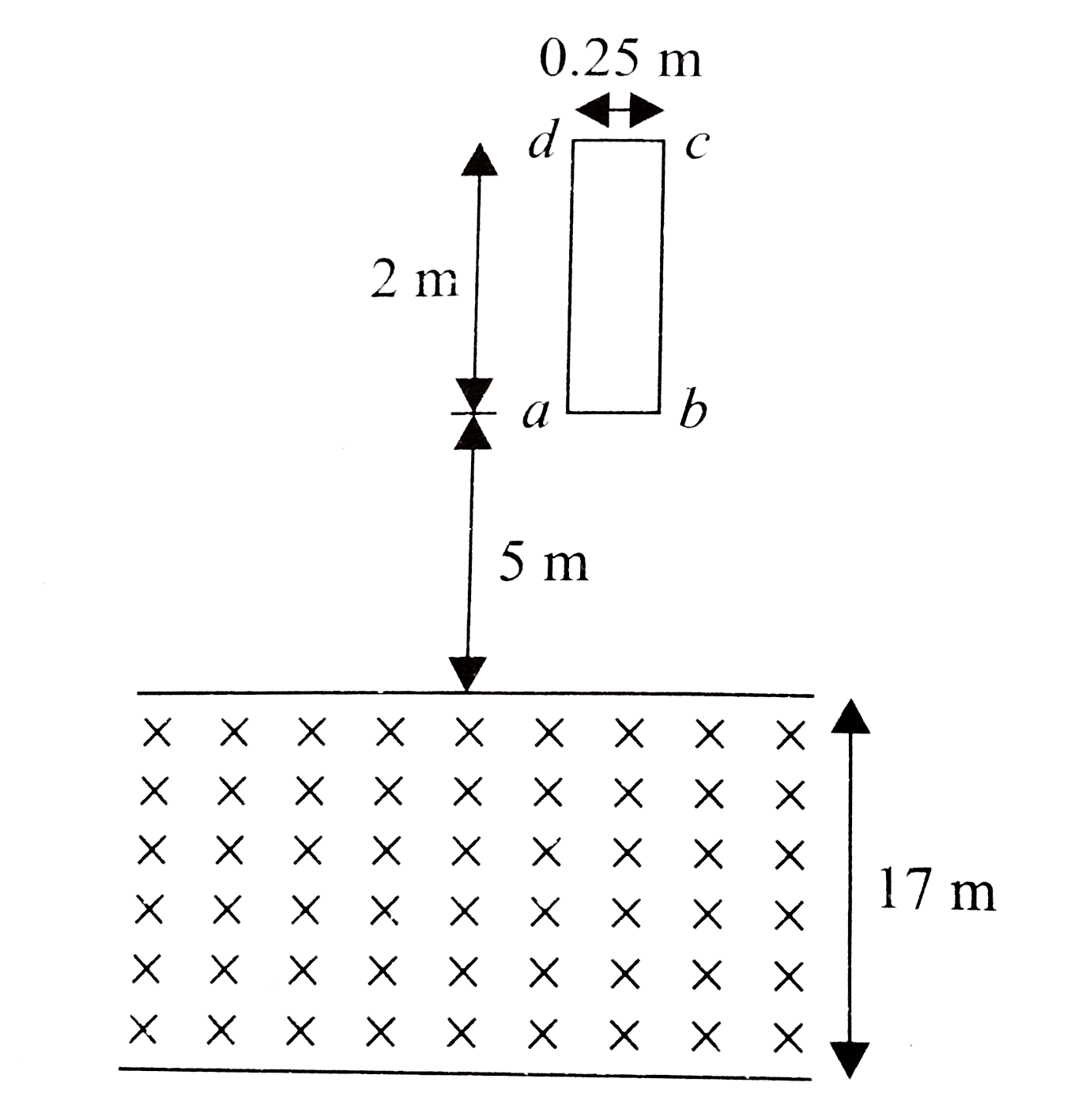
A rectangular wire frame of dimensions (0.25×2.0m) and mass 0.5 kg falls from a height 5m above a region occupied by uniform magnetic field of magnetic induction 1 T. The resistance of the wire frame is 18(Ω). Find
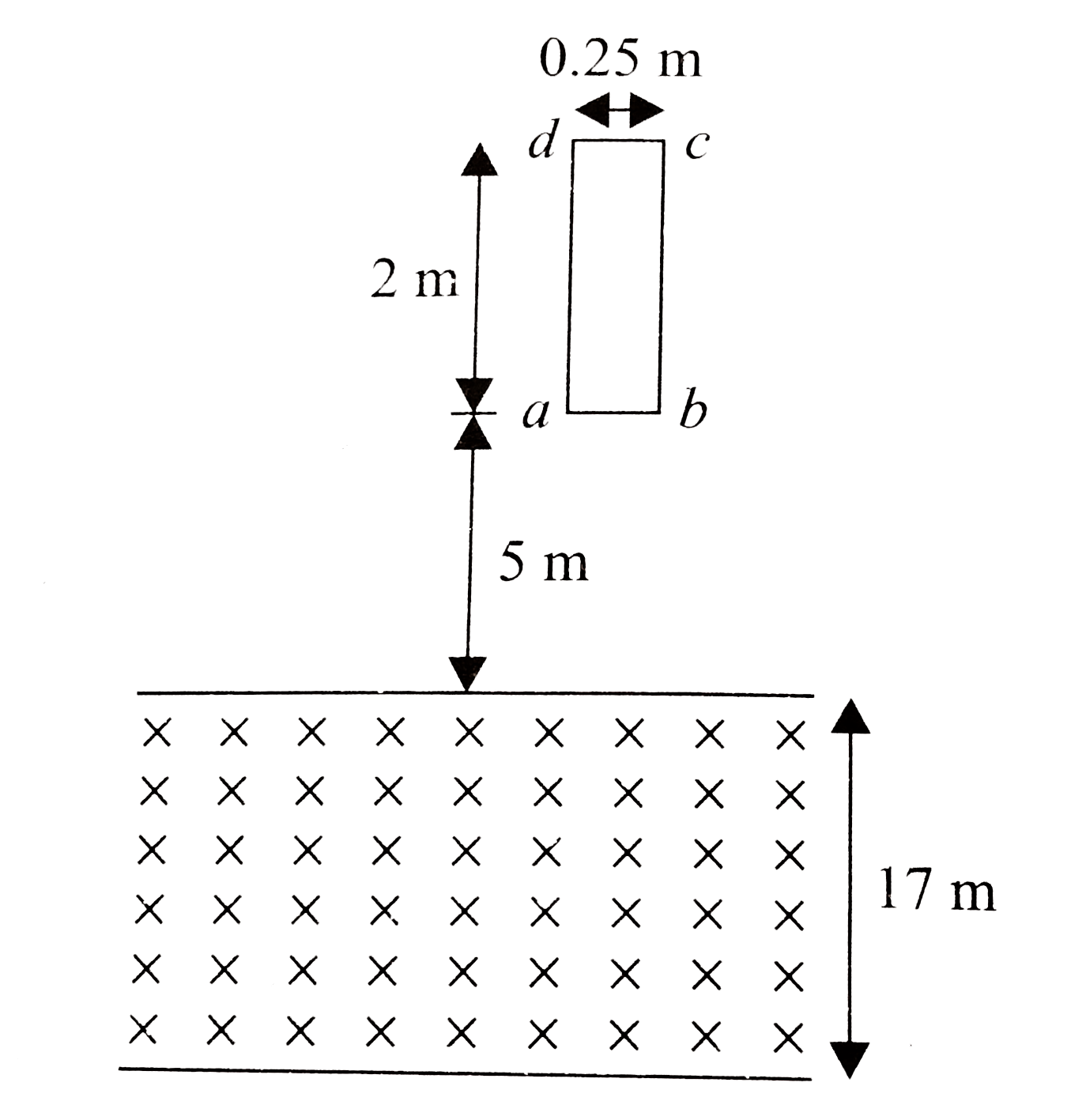
time taken by the wire frame when it just starts coming out of the magnetic field.View SolutionQuestion 200
A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
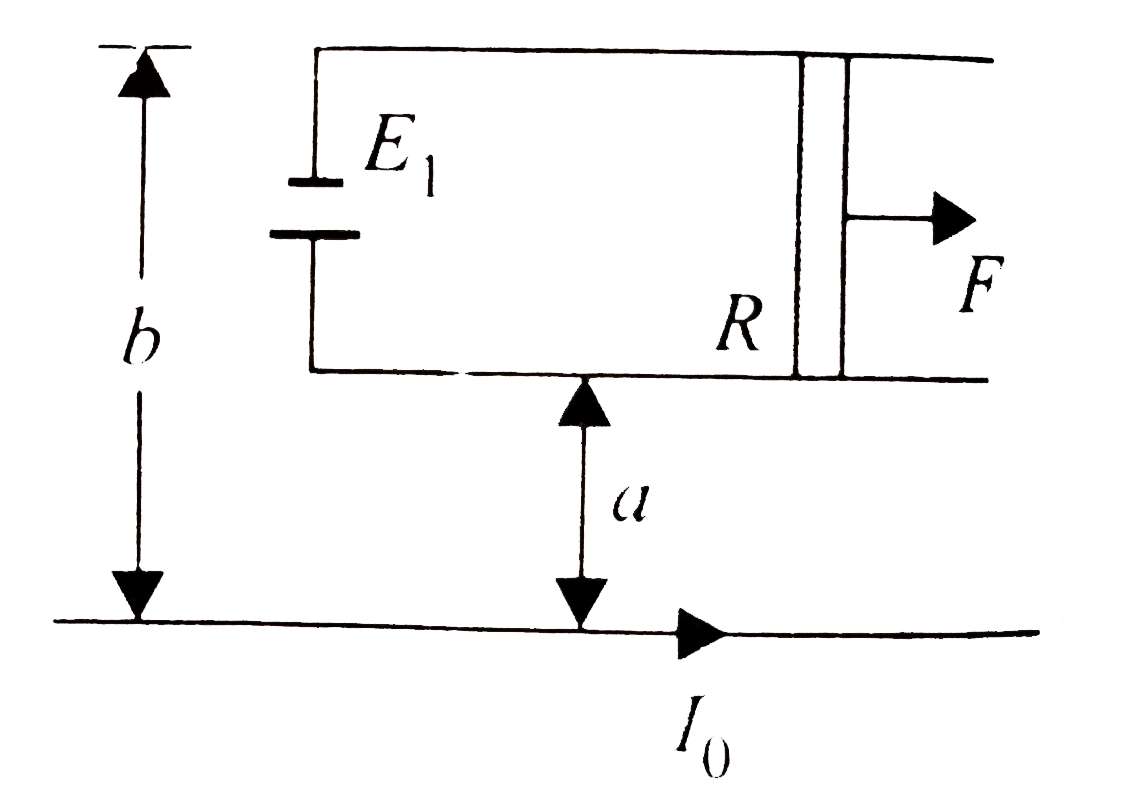
Find the value of current in the circuit if the rod slides with constant velocity v0View SolutionQuestion 201
A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
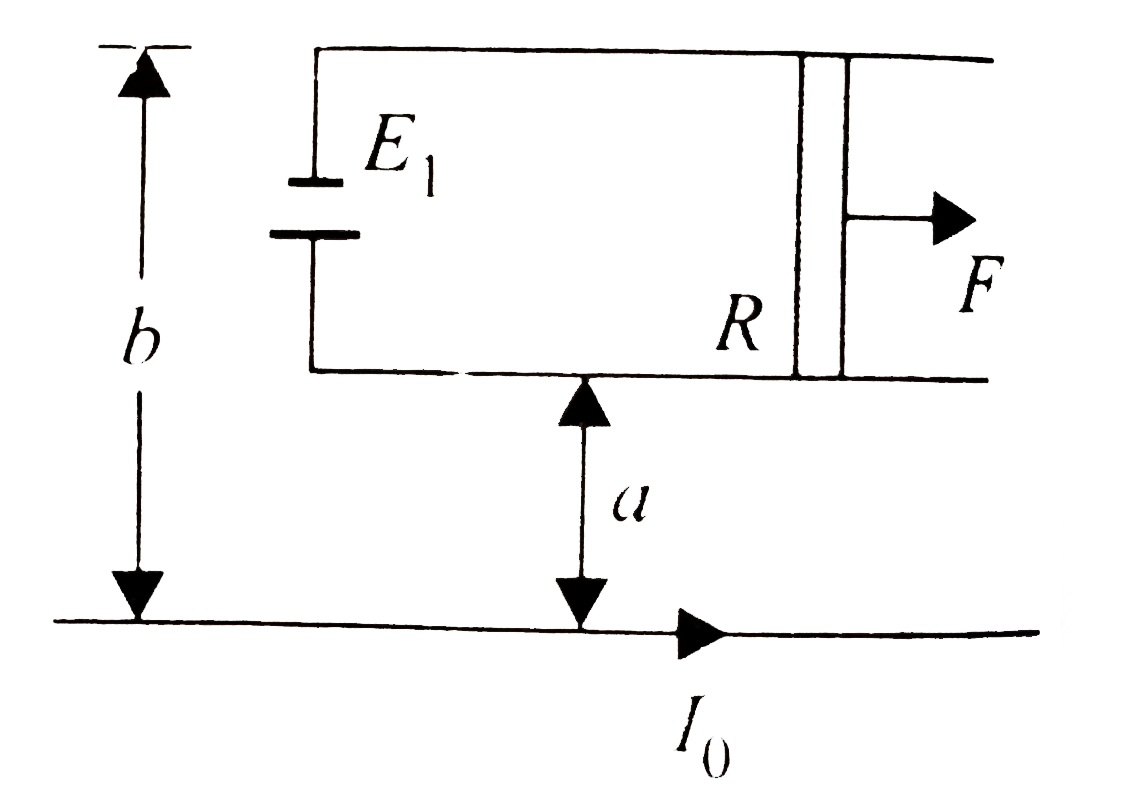
Find the value of F if the rod slides with constant velocityView SolutionQuestion 202
A stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.View SolutionQuestion 203
A stationary circular loop of radius a is located in a magnetic field which varies with time from t = 0 to t = T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
magnitude of charge flown through the loop from instant t = 0 to the instant when current reverses its direction.View SolutionQuestion 204
A circular ring of radius a is made from a wire having resistance (λ) per unit length. The ring is mounted on a car such that ring remains vertical. The care moves along a horizontal circle of radius R and completes n revolutions per minute. The horizontal component of earth's magnetic field be H,
The emf induced in the ring is View SolutionQuestion 205
A circular ring of radius a is made from a wire having resistance (λ) per unit length. The ring is mounted on a car such that ring remains vertical. The care moves along a horizontal circle of radius R and completes n revolutions per minute. The horizontal component of earth's magnetic field be H,
Calculate average rate at which heat is produced in the ring View SolutionQuestion 206
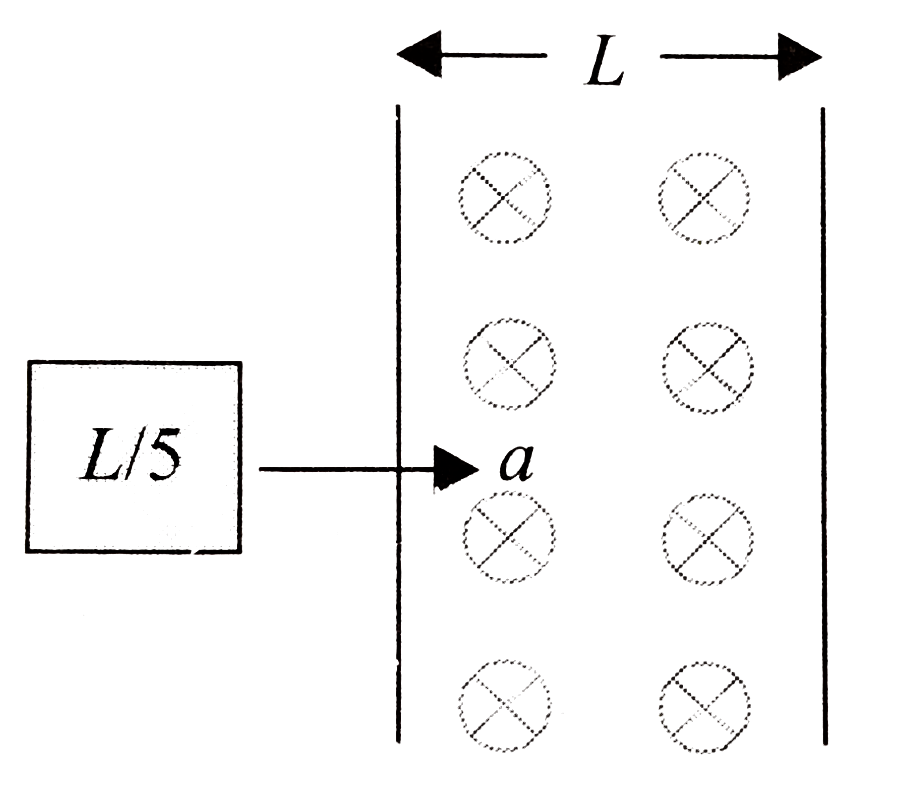
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
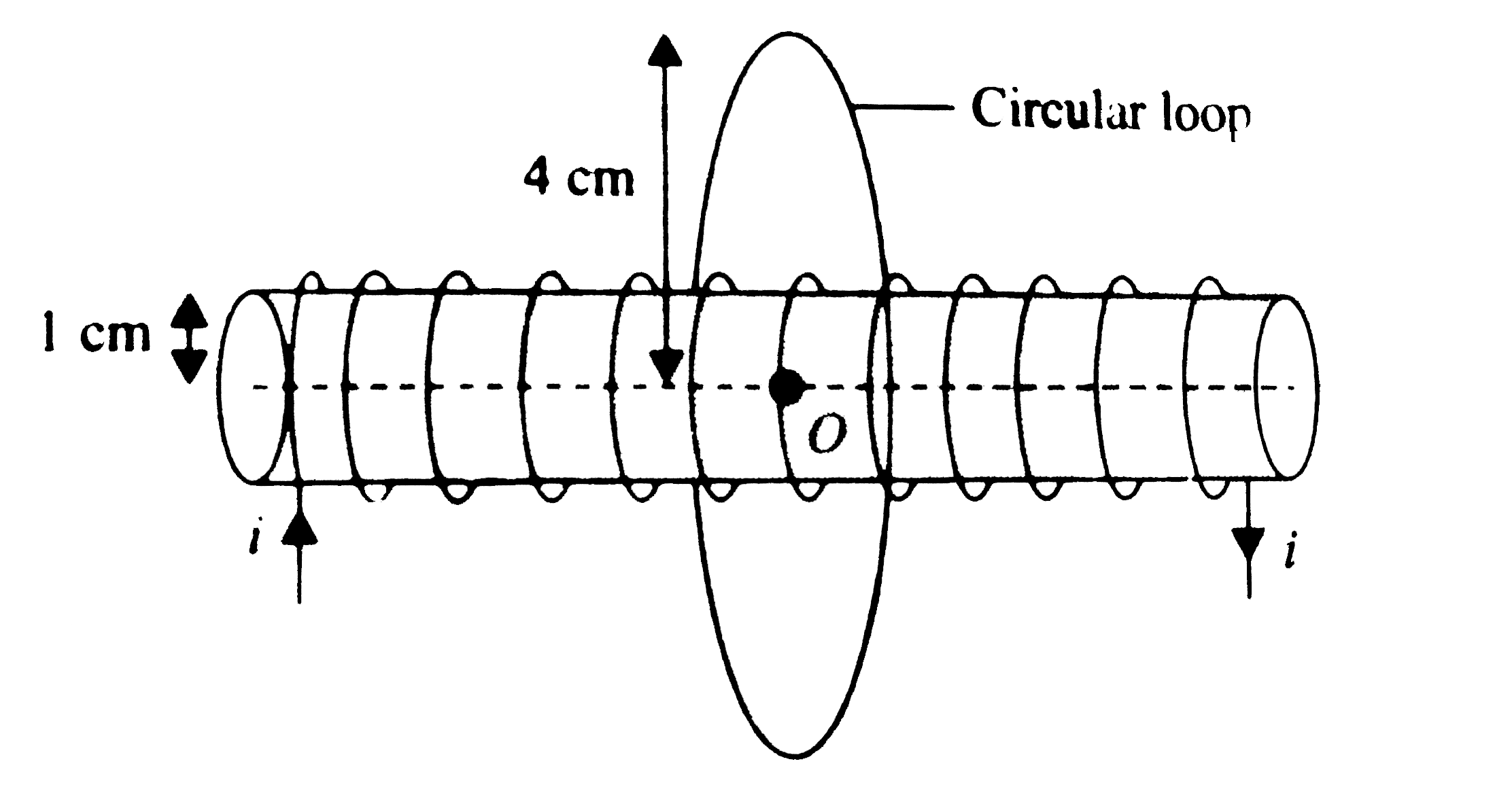
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magnitude of induced current that appears in the circular loop is View SolutionQuestion 207
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magnetic of induced electric field strength in the circular loop is nearly We know that there is magnetic flux through the circular loop because of the magnetic field of current in the solenoid. For the purpose of circular loop, let us call it the external magnetic field. As current in the solenoid is reducing, external magnetic field for the circular loop also reduced resulting in induced current in the loop. Finally, as the solenoid current becomes zero, external field for the loop also becomes zero and stop changing. However, induced current in the loop will not stop at the instant at which the external field stops changing. This is because induced current itself produces a magnetic field that results in a flux through the loop. External field becoming zero without any further change will compel the induced current in the loop to become zero and so magnetic flux through the loop due to change in induced current will also change resulting in a further induced phenomenon that sustains currents in the loop even after the external field becomes zero.View SolutionQuestion 208
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoidView SolutionQuestion 209
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre View SolutionQuestion 213
Consider the circuit shown below. When switch S1 is closed, let I be the current at time t, then applying Kirchhoff's law
E−iR−Ldidt=0or∫i0diE−iR=1L∫10dt
i=ER(1−e−Rl⋅t)
LR = time constant of circuit
When current reaches its steady value (=i0, open S1 and close S2, the current does reach to zero finally but decays expnentially. The decay equation is given as i=i0e−RL⋅T).
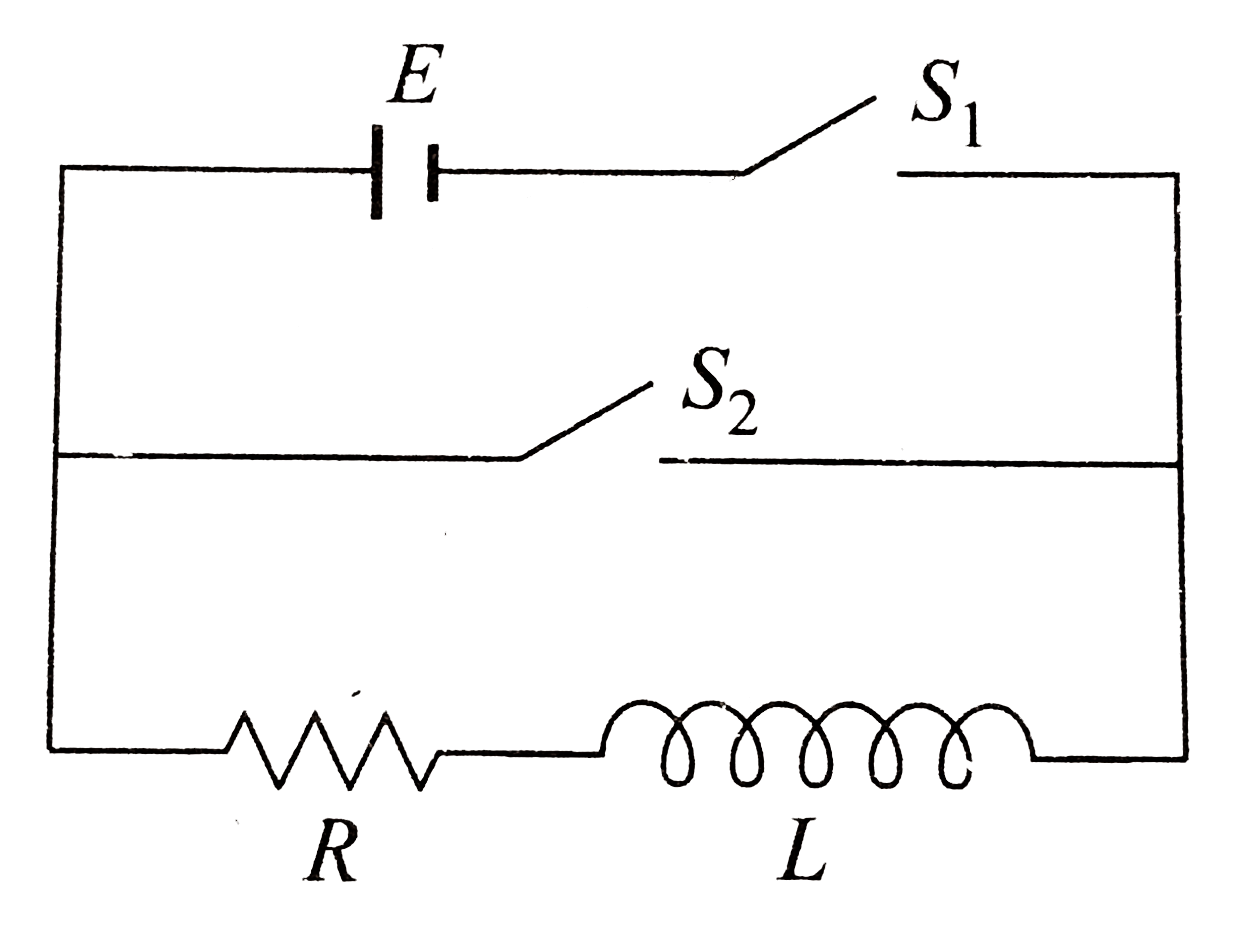
When a coil carrying a steady current is short circuited, the current decreases in it η times in time t0. The time constant of the circuit is View SolutionQuestion 214
Consider the circuit shown below. When switch S1 is closed, let I be the current at time t, then applying Kirchhoff's law
E−iR−Ldidt=0or∫i0diE−iR=1L∫10dt
i=ER(1−e−Rl⋅t)
LR = time constant of circuit
When current reaches its steady value (=i0, open S1 and close S2, the current does reach to zero finally but decays expnentially. The decay equation is given as i=i0e−RL⋅T.

Three idenctical rings. The first (a). slips without rolling and the second (b) rolls without slipping and the third rolls with slipping .View SolutionQuestion 215
Consider the circuit shown below. When switch S1 is closed, let I be the current at time t, then applying Kirchhoff's law
E−iR−Ldidt=0or∫i0diE−iR=1L∫10dt
i=ER(1−e−Rl⋅t)
LR = time constant of circuit
When current reaches its steady value (=i0, open S1 and close S2, the current does reach to zero finally but decays expnentially. The decay equation is given as i=i0e−RL⋅T.

A wire is sliding as shown in fig . The angle between the acceleration and velocity of the wire is
 View Solution
View SolutionQuestion 216
Two long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.

A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The current in the wire MN is View SolutionQuestion 217
Two long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.

A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The force required to pull the ring with uniform velocity v is View SolutionQuestion 218
A uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
Net Induced EMF (in Volt) on conducting ring as function of time is View SolutionQuestion 219
A uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
Time (in second) at which ring start toppling isView SolutionQuestion 220
A uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then

Net Induced EMF (in Volt) on conducting ring as function of time is View SolutionQuestion 221
A uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then

Net Induced EMF (in Volt) on conducting ring as function of time is View SolutionQuestion 222
A charged particle enters a uniform magnetic field with velocity v0=4m/s perpendicular to it, the length of magnetic field is x=(√32)R, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.View SolutionQuestion 223
A charged particle of mass m = 1 mg and charge q=1(μ)C enter along AB at point A in a uniform magnetic field B = 1.2 T existing in the rectangular region of size a×b, where a = 4 m and b = 3 m. The particle leaves the region exactly at corner point C. What is the speed v(∈ms−1) of the particle?
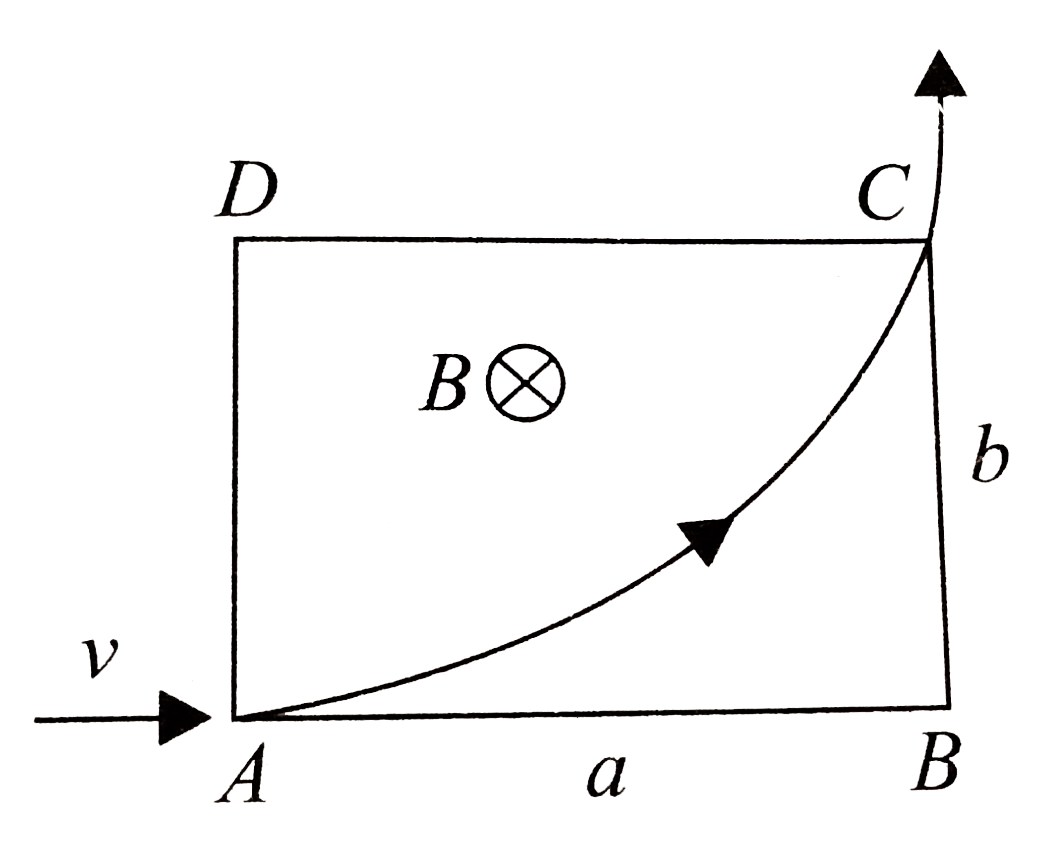 View Solution
View SolutionQuestion 225
A conducting rod of mass 200 gm and length 10 cm can slide without friction on two long, horizontal rails. A uniform magnetic field of magnitude 5 m T exists in the region as shown. A source S is used to maintain a constant current 2 A through the rod. If motion of the rod starts from the rest, find its speed (in cm/s) after 10 s from the start of the motion
 View Solution
View SolutionQuestion 226
An infinitely long conductor PQR is bent to form a right angle as shown. A current I flows through PQR. The magnetic field due to this current at the point MisB1. Now, another infinitely long straight conductor QS is connected at Q so that the current is I/2 in QR as well as in QS, the current in PQ remaining unchanged. The magnetic field at M is now B2=4mT. Find the value of B1(inmT).
 View Solution
View SolutionQuestion 227
A magnetic field →B=−B0ˆi exists within a sphere of radius R=v0T√3 where T is the time period of one revolution of a charged particle starting its motion form origin and moving with a velocity vce(v)0=v02√3ˆi−v02ˆj. Find the number of turns that the particle will take to come out of the magnetic field. View SolutionQuestion 232
The diagram shows a circuit having a coil of resistance R=2.5(Ω) and inductance L connected to a conducting rod PQ which can slide on perfectly conducting circular ring of radius 10 cm with its centre at 'P'. Assume that friction and gravity are absent and a constant uniform magnetic field of 5 T exist as shown in Fig.
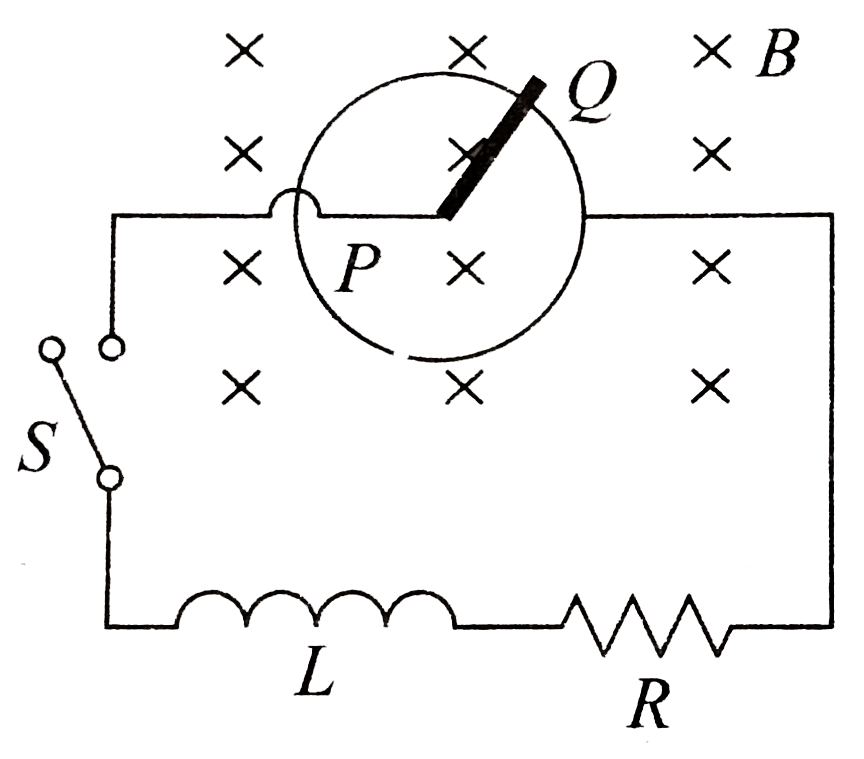
At t = 0, the circuit is switched on and simultaneously a time varying external torque is applied on the rod so that it rotates about P with a constant angular velocity 40rad/s. Find magnitude of this torque (in milli Nm) when current reaches half of its maximum value. Neglect the self-inductance of the loop formed by the circuit.View SolutionQuestion 233
A thin wire AC shaped as a semi-circle of diameter d rotates with a constant angular frequency (ω) in a uniform magnetic field of indcution →B. The vector →ω is parallel to →B and the rotation axis XY passes through the end A of the wire and is perpendicular to the diameter AC (see Fig.). →B is directed left to right in the plane of the paper. The value of the line intergral I=∫→E⋅d→r taken along the wire form the point A to the point C will be ωBd2?. What interger should be inserted in place of question mark.
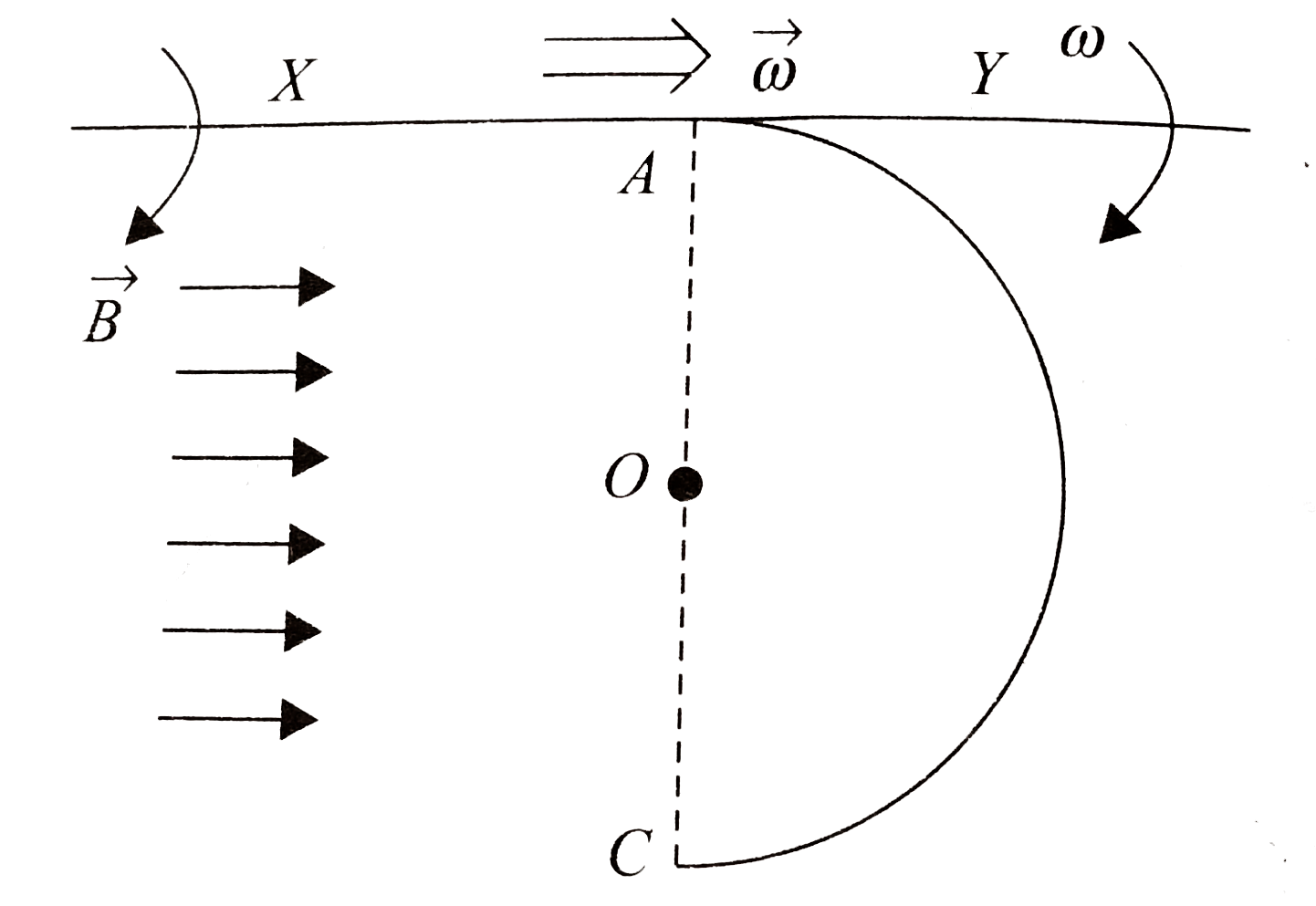 View Solution
View Solution










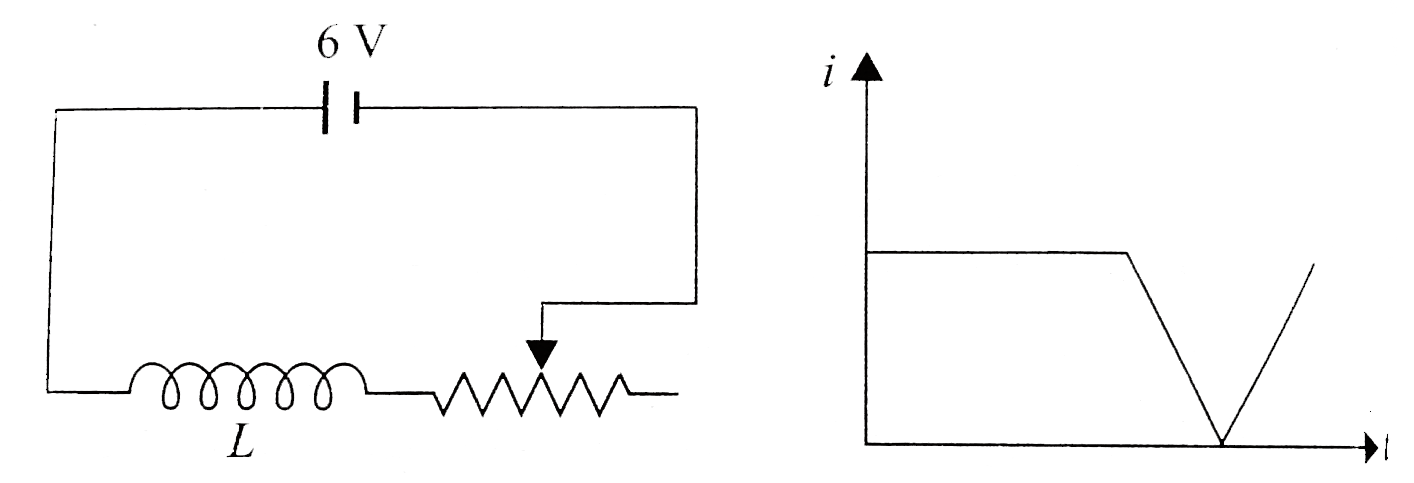










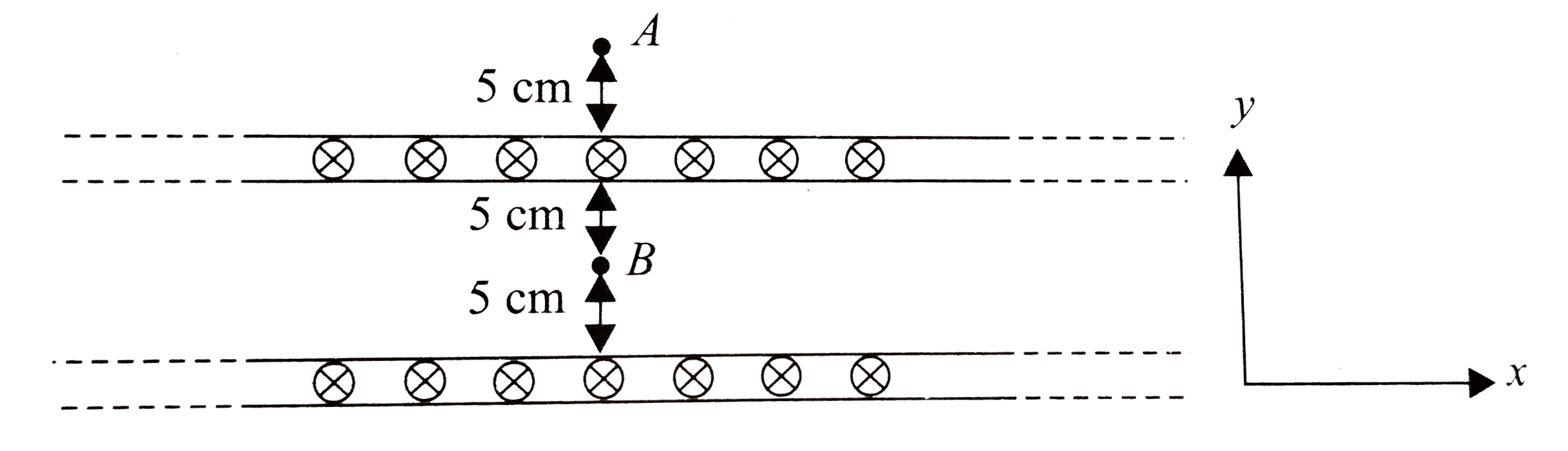

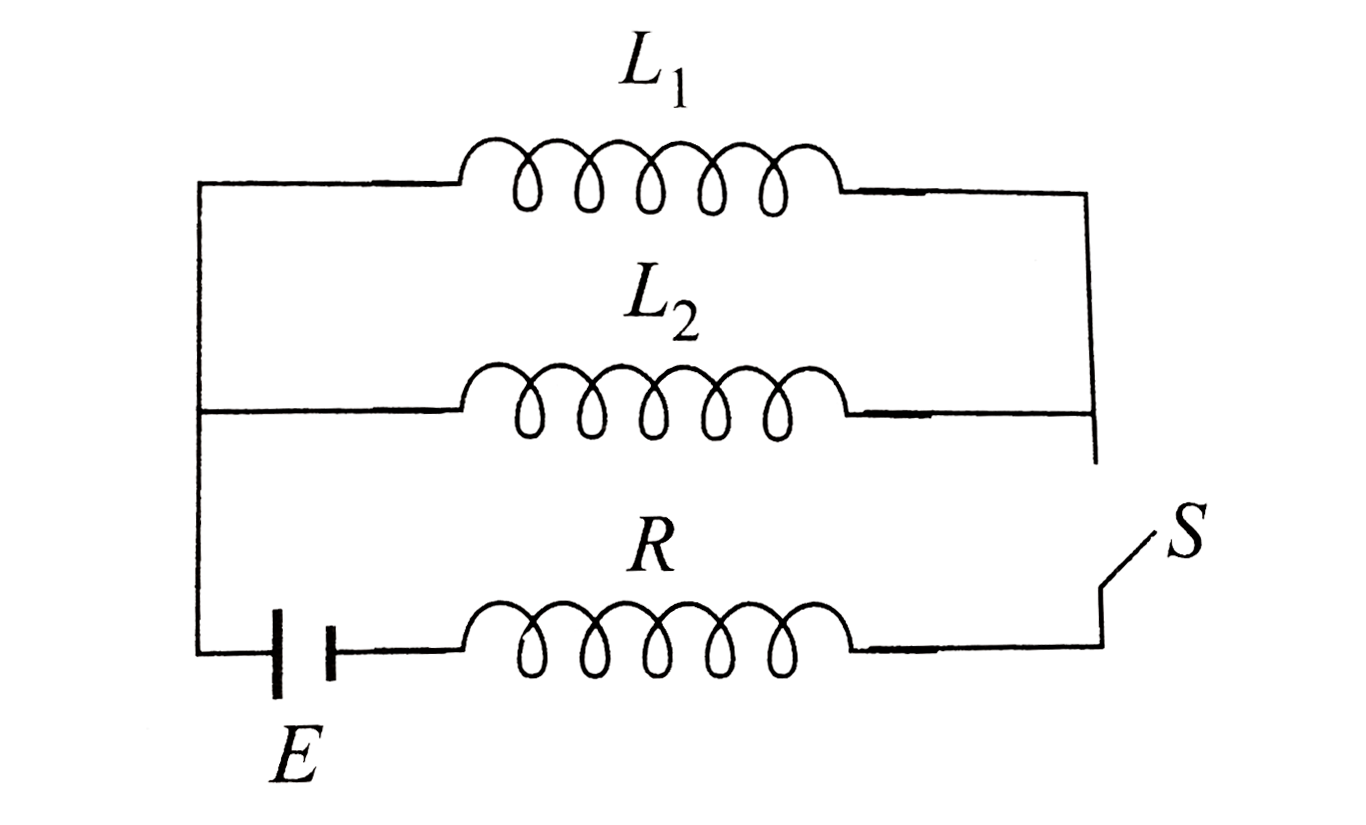


 .
.