Exercise (Comprehension) from CENGAGE AREA for Class 12

Class 12	MATHS
Chapter	AREA
CENGAGE	Exercise (Comprehension)
Medium	English
Academic Year	2023-2024

Question 1
Let $A_{r}$ be the area of the region bounded between the curves $y^{2} = (e^{- k r}) x (where k > 0, r \in N) and the line y = m x (where m \neq 0)$ , k and m are some constants
$A_{1}, A_{2}, A_{3}, \dots$ are in G.P. with common ratio View Solution
Question 2
Let $A_{r}$ be the area of the region bounded between the curves $y^{2} = (e^{- k r}) x (where k > 0, r \in N) and the line y = m x (where m \neq 0)$ , k and m are some constants
$lim n \to \infty Σ_{i = 1}^{n} A_{i} = \frac{1}{48 (e^{2 k} - 1)}$ then the value of m is View Solution
Question 3
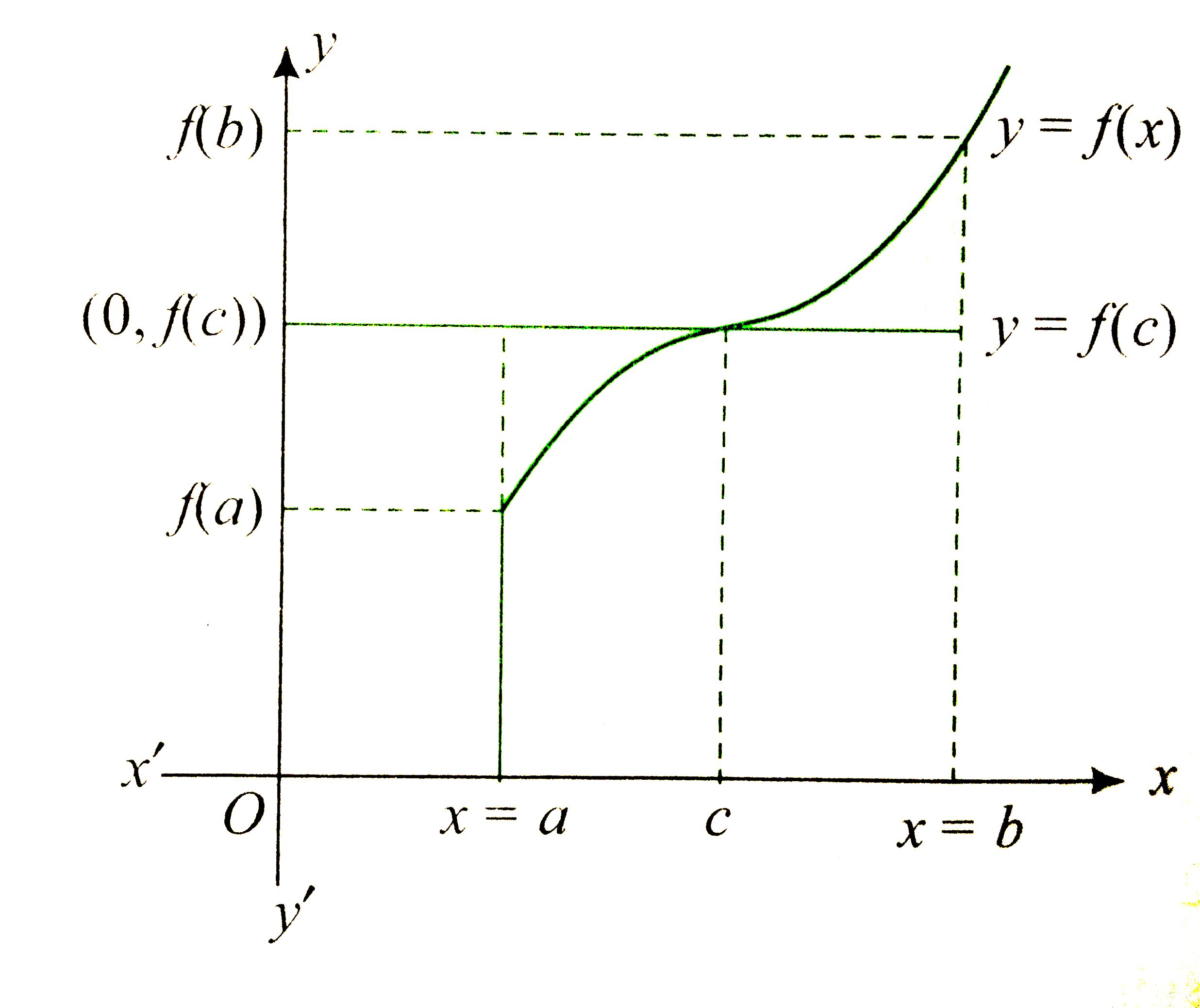
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at $x = a, x = b, y = f (x) and y = f (c) (where c \in (a, b)) is minimum when c = \frac{a + b}{2}$ .
$Proof : A = \int_{a}^{c} (f (c) - f (x)) d x + \int_{c}^{b} (f (c)) d x$
$= f (c) (c - a) - \int_{a}^{c} (f (x)) d x + \int_{a}^{b} (f (x)) d x - f (c) (b - c)$
$\Rightarrow A = [2 c - (a + b)] f (c) + \int_{c}^{b} (f (x)) d x - \int_{a}^{c} (f (x)) d x$

Differentiating w.r.t. c, we get
$\frac{d A}{d c} = [2 c - (a + b)] f' (c) + 2 f (c) + 0 - f (c) - (f (c) - 0)$
For maxima and minima , $\frac{d A}{d c} = 0$
$\Rightarrow f' (c) [2 c - (a + b)] = 0 (a s f' (c) \neq 0)$
Hence, $c = \frac{a + b}{2}$
$Also for c < \frac{a + b}{2}, \frac{d A}{d c} < 0 and for c > \frac{a + b}{2}, \frac{d A}{d c} > 0$
Hence, A is minimum when $c = \frac{a + b}{2}$ .
If the area bounded by $f (x) = \frac{x^{3}}{3} - x^{2} + a$ and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is View Solution
Question 4
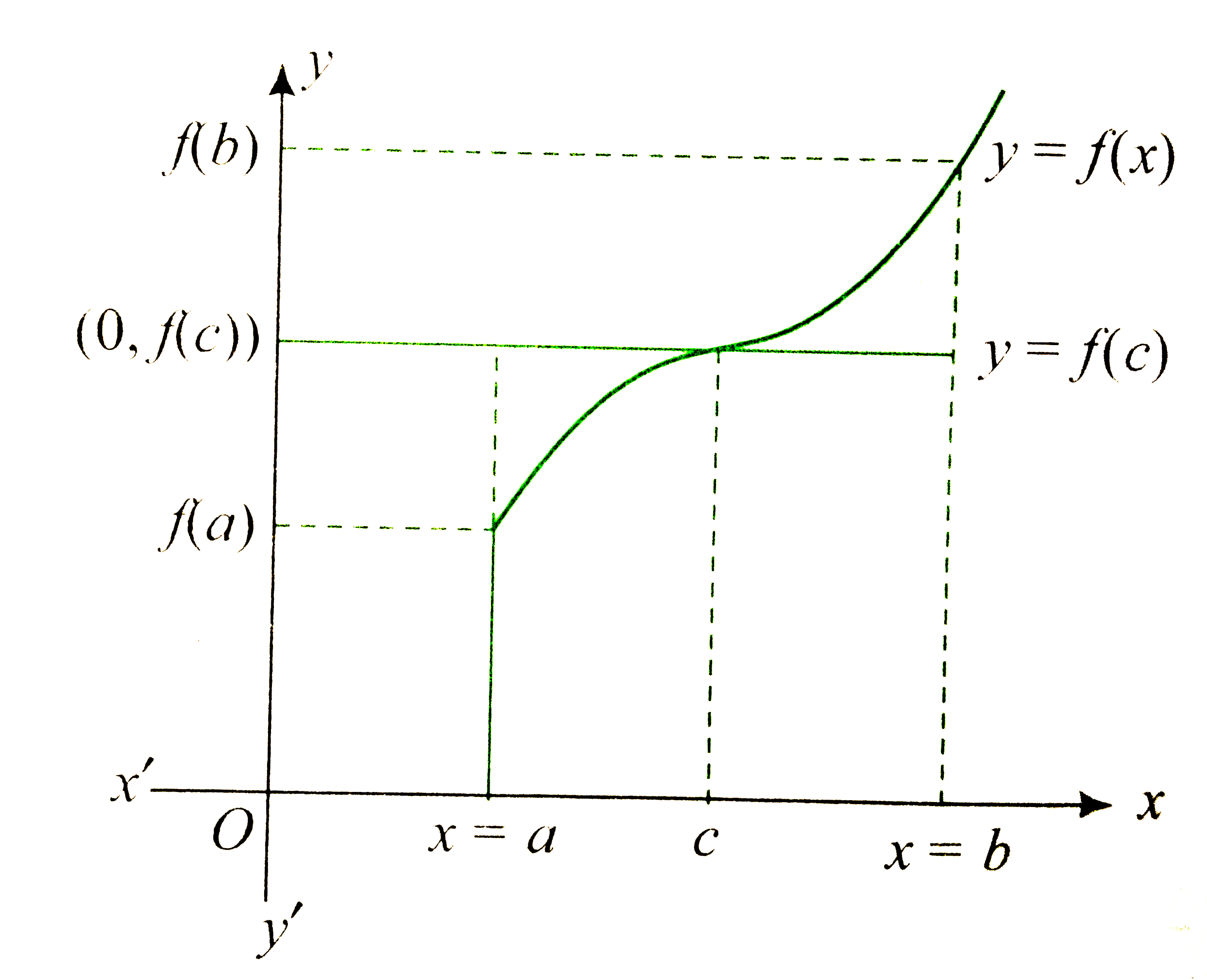
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at $x = a, x = b, y = f (x) and y = f (c) (where c \in (a, b)) is minimum when c = \frac{a + b}{2}$ .
$Proof : A = \int_{a}^{c} (f (c) - f (x)) d x + \int_{c}^{b} (f (c)) d x$
$= f (c) (c - a) - \int_{a}^{c} (f (x)) d x + \int_{a}^{b} (f (x)) d x - f (c) (b - c)$
$\Rightarrow A = [2 c - (a + b)] f (c) + \int_{c}^{b} (f (x)) d x - \int_{a}^{c} (f (x)) d x$

Differentiating w.r.t. c, we get
$\frac{d A}{d c} = [2 c - (a + b)] f' (c) + 2 f (c) + 0 - f (c) - (f (c) - 0)$
For maxima and minima , $\frac{d A}{d c} = 0$
$\Rightarrow f' (c) [2 c - (a + b)] = 0 (a s f' (c) \neq 0)$
Hence, $c = \frac{a + b}{2}$
$Also for c < \frac{a + b}{2}, \frac{d A}{d c} < 0 and for c > \frac{a + b}{2}, \frac{d A}{d c} > 0$
Hence, A is minimum when $c = \frac{a + b}{2}$ .
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function $y = x^{3} + 3 x^{2} + x + a$ , and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is View Solution
Question 5
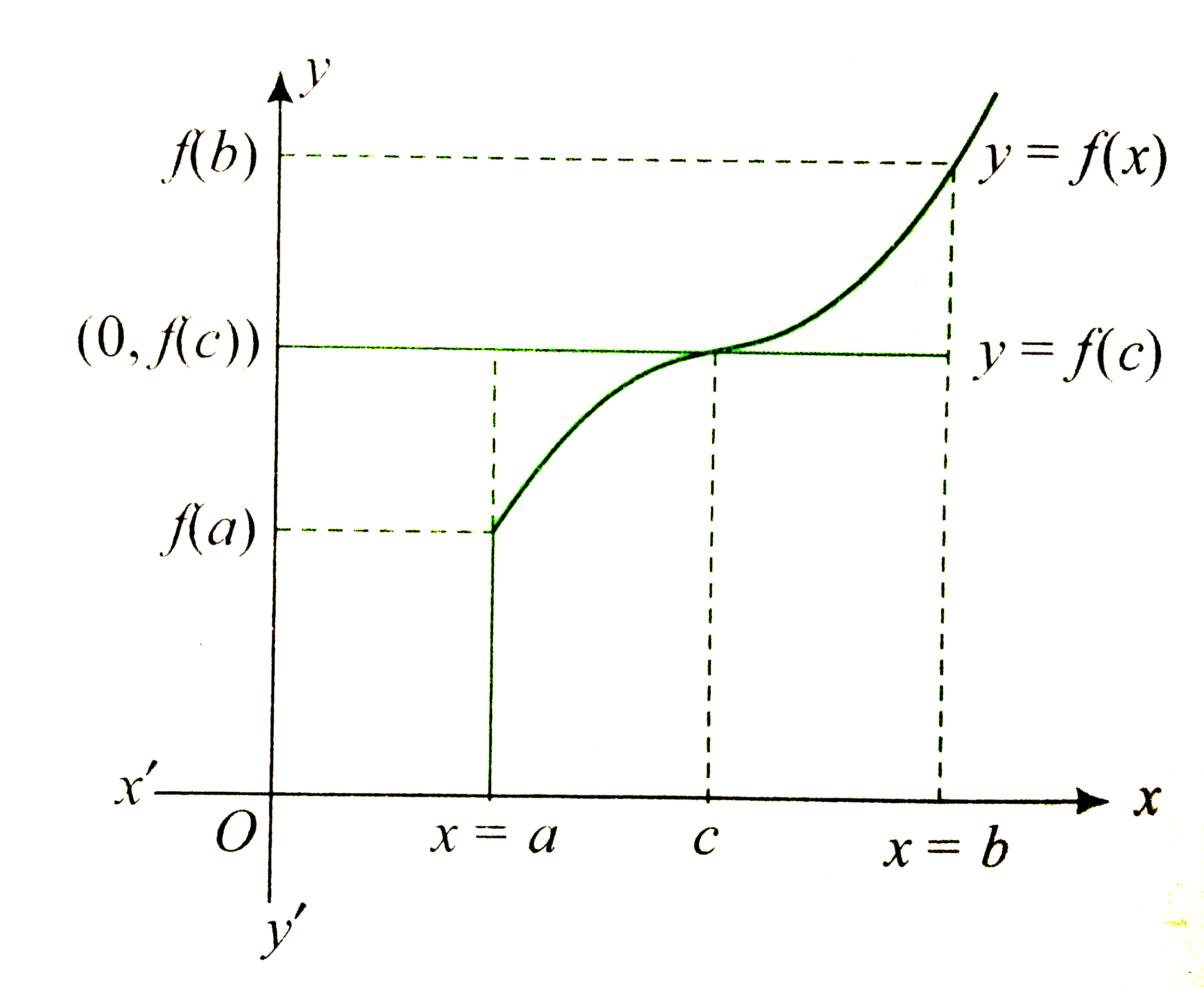
If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at $x = a, x = b, y = f (x) and y = f (c) (where c \in (a, b)) is minimum when c = \frac{a + b}{2}$ .
$Proof : A = \int_{a}^{c} (f (c) - f (x)) d x + \int_{c}^{b} (f (c)) d x$
$= f (c) (c - a) - \int_{a}^{c} (f (x)) d x + \int_{a}^{b} (f (x)) d x - f (c) (b - c)$
$\Rightarrow A = [2 c - (a + b)] f (c) + \int_{c}^{b} (f (x)) d x - \int_{a}^{c} (f (x)) d x$

Differentiating w.r.t. c, we get
$\frac{d A}{d c} = [2 c - (a + b)] f' (c) + 2 f (c) + 0 - f (c) - (f (c) - 0)$
For maxima and minima , $\frac{d A}{d c} = 0$
$\Rightarrow f' (c) [2 c - (a + b)] = 0 (a s f' (c) \neq 0)$
Hence, $c = \frac{a + b}{2}$
$Also for c < \frac{a + b}{2}, \frac{d A}{d c} < 0 and for c > \frac{a + b}{2}, \frac{d A}{d c} > 0$
Hence, A is minimum when $c = \frac{a + b}{2}$ .
If the area enclosed by $f (x) = sin x + cos x, y = a$ between two consecutive points of extremum is minimum, then the value of a is View Solution
Question 6
Consider the area $S_{0}, S_{1}, S_{2} \dots .$ bounded by the x-axis and half-waves of the curve $y = e^{- x} sin x, where x \geq 0 .$
The value of $S_{0}$ is View Solution
Question 7
Consider the sequence of natural numbers $s_{0}, s_{1}, s_{2}$ ,... such that $s_{0} = 3, s_{1} = 3 and s_{n} = 3 + s_{n - 1} s_{n - 2}$ , then View Solution
Question 8
Consider the area $S_{0}, S_{1}, S_{2} \dots .$ bounded by the x-axis and half-waves of the curve $y = e^{- x} sin x, where x \geq 0 .$
$Σ_{n = 0}^{\infty} S_{n}$ is equal to View Solution
Question 9
$Two curves C_{1} \equiv {[f (y)]}^{2 / 3} + {[f (x)]}^{1 / 3} = 0 and C_{2} \equiv {[f (y)]}^{2 / 3} + {[f (x)]}^{2 / 3} = 12, satisfying the relation (x - y) f (x + y) - (x + y) f (x - y) = 4 x y (x^{2} - y^{2})$
The area bounded by $C_{1} and C_{2}$ is View Solution
Question 10
Two curves C_(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C_(2)equiv[f(y)]^(2//3)+[f(x)]^(2//3)=12, satisfying the relation "(x-y)f(x+y)-(x+y)f(x-y)=4xy(x^(2)-y^(2))
The area bounded by the curve C_(2) and |x|+|y|=sqrt(12) is View Solution
Question 11
Two curves C_(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C_(2)equiv[f(y)]^(2//3)+[f(x)]^(2//3)=12, satisfying the relation "(x-y)f(x+y)-(x+y)f(x-y)=4xy(x^(2)-y^(2))
The area bounded by C_(1) and x+y+2=0 is View Solution
Question 12
Consider the two curves $C_{1} : y = 1 + cos x and C_{2} : y = 1 + cos (x - α) for α \in (0, \frac{π}{2}), where x \in [0, π] .$ Also the area of the figure bounded by the curves $C_{1}, C_{2}, and x = 0$ is same as that of the figure bounded by $C_{2}, y = 1, and x = π$ .
The value of $α$ is View Solution
Question 13
Consider two curves $C_{1} : y = \frac{1}{x}$ and $C_{2} . y = ln x$ on the $x y$ plane. Let $D_{1}$ , denotes the region surrounded by $C_{1}, C_{2}$ and the line $x = 1$ and $D_{2}$ denotes the region surrounded by $C_{1}, C_{2}$ and the line $x = a$ , Find the value of $a$ View Solution
Question 14
Consider the function defined implicity by the equation $y^{2} - 2 y e^{{sin}^{- 1} x} + x^{2} - 1 + [x] + e^{2 {sin}^{- 1} x} = 0 (where [x] denotes the greatest integer function) .$
Line x=0 divides the region mentioned above in two parts. The ratio of area of left-hand side of line to that of right-hand side of line is View Solution
Question 15
Consider the function defined implicity by the equation $y^{2} - 2 y e^{{sin}^{- 1} x} + x^{2} - 1 + [x] + e^{2 {sin}^{- 1} x} = 0 (where [x] denotes the greatest integer function) .$
Line x=0 divides the region mentioned above in two parts. The ratio of area of left-hand side of line to that of right-hand side of line is View Solution
Question 16
Consider two functions
$f (x) = {\begin{matrix} [x], & - 2 \leq x \leq - 1 | x | + 1, & - 1 < x \leq 2 \end{matrix} and g (x) = {\begin{matrix} [x], & - π \leq x < 0 sin x, & 0 \leq x \leq π \end{matrix}$
where [.] denotes the greatest integer function.
The exhaustive domain of $g (f (x))$ is View Solution
Question 17
Computing area with parametrically represented boundaries : If the boundary of a figure is represented by parametric equation, i.e., $x = x (t), y = y (t),$ then the area of the figure is evaluated by one of the three formulas :
$S = - \int_{α}^{β} y (t) x' (t) d t,$
$S = \int_{α}^{β} x (t) y' (t) d t,$
$S = \frac{1}{2} \int_{α}^{β} (x y' - y x') d t,$
Where $α and β$ are the values of the parameter t corresponding respectively to the beginning and the end of the traversal of the curve corresponding to increasing t.
The area of the region bounded by an are of the cycloid $x = a (t - sin t), y = a (1 - cos t)$ and the x-axis is View Solution
Question 18
Computing area with parametrically represented boundaries : If the boundary of a figure is represented by parametric equation, i.e., $x = x (t), y = y (t),$ then the area of the figure is evaluated by one of the three formulas :
$S = - \int_{α}^{β} y (t) x' (t) d t,$
$S = \int_{α}^{β} x (t) y' (t) d t,$
$S = \frac{1}{2} \int_{α}^{β} (x y' - y x') d t,$
Where $α and β$ are the values of the parameter t corresponding respectively to the beginning and the end of the traversal of the curve corresponding to increasing t.
The area of the loop described as
$x = \frac{t}{3} (6 - t), y = \frac{t^{2}}{8} (6 - t)$ is View Solution
Question 19
Computing area with parametrically represented boundaries : If the boundary of a figure is represented by parametric equation, i.e., $x = x (t), y = y (t),$ then the area of the figure is evaluated by one of the three formulas :
$S = - \int_{α}^{β} y (t) x' (t) d t,$
$S = \int_{α}^{β} x (t) y' (t) d t,$
$S = \frac{1}{2} \int_{α}^{β} (x y' - y x') d t,$
Where $α and β$ are the values of the parameter t corresponding respectively to the beginning and the end of the traversal of the curve corresponding to increasing t.
If the curve given by parametric equation $x = t - t^{3}, y = 1 - t^{4}$ forms a loop for all values of $t \in [- 1, 1]$ then the area of the loop is View Solution
Question 20
Let f(x) be a continuous function fiven by $f (x) = {\begin{matrix} 2 x, & | x | \leq 1 x^{2} + a x + b, & | x | > 1 \end{matrix}, then$
If f(x) is continuous for all real x then the value of $a^{2} + b^{2}$ is View Solution
Question 21
Let $f (x)$ be continuous function given by $f (x) = {2 x, | x | \leq 1 x^{2} + a x + b, | x | > 1} .$ Find the area of the region in the third quadrant bounded by the curves $x = - 2 y^{2} a n d y = f (x)$ lying on the left of the line $8 x + 1 = 0 .$ View Solution

All Exercises from CENGAGE Class 12 MATHS AREA

Home
Ask Doubt
Profile