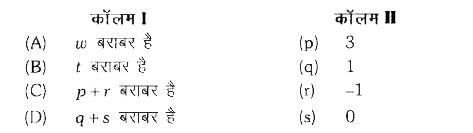ERRORLESS MATHS (HINDI) सारणिक तथा आव्यूह की JEE ADVANCED MORE THAN ONE CORRECT ANSWERS कक्षा 12 के लिए
| कक्षा 12 | गणित |
| Chapter | सारणिक तथा आव्यूह |
| ERRORLESS MATHS (HINDI) | JEE ADVANCED MORE THAN ONE CORRECT ANSWERS |
| माध्यम | हिंदी |
| शैक्षणिक वर्ष | 2023-2024 |
Question 45
माना की S उन सभी स्तम्भ आव्यूहों ⎡⎢⎣b1b2b3⎤⎥⎦का समुच्चय है जिनके लिए b1,b2,b3∈R और वास्तविक चरो
−x+2y+5z=b1
2x−4y+3z=b2
x−2y+2z=b3 वाले समीकरण निकाय का कम से कम एक हल है। तब निम्नलिखित वास्तविक चरो वाले निकायों में से किस (कौन से ) निकाय (निकाय ) का भी प्रत्येक ⎡⎢⎣b1b2b3⎤⎥⎦∈S के लिए कम से कम एक हल है ?हल देखेंQuestion 46
माना कि S उन सभी स्तम्भ आव्यूहों ⎡⎢⎣b1b2b3⎤⎥⎦ का समुच्चय है जिनके लिए b1,b2,b2∈R और वास्तविक चरों वाले समीकरणों के निकाय −x+2y+5z=b1
2x−4y+3z=b2
x−2y+2z=b3
का कम से कम एक हल है, तब निम्नलिखित वास्तविक चरों वाले निकायों में से किस (कौन से ) निकाय (निकायों ) का भी प्रत्येक ⎡⎢⎣b1b2b3⎤⎥⎦∈S के लिए कम से कम एक हल है हल देखेंQuestion 65
कथन-1 : उभयनिष्ठ अनुपात r1 के साथ a,b,c गु. श्रे. में तथा उभयनिष्ठ अनुपात r2 के साथ α,β,γ गु. श्रे. में है, यदि समीकरणों ax+αy+z=0,bx+βy+z=0,cx+γy+z=0 के केवल अशून्य हल है, तो r1≠r2,r1,r2≠1
कथन-2 : समीकरणों a1x+b1y+c1z=0,a2x+b2y+c2z=0,a3x+b3y+c3z=0 के केवल अशून्य हल है यदि ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣≠0हल देखेंQuestion 66
कथन-1 : उभयनिष्ठ अनुपात r1 के साथ a,b,c गु. श्रे. में तथा उभयनिष्ठ अनुपात r2 के साथ α,β,γ गु. श्रे. में है, यदि समीकरणों ax+αy+z=0,bx+βy+z=0,cx+γy+z=0 के केवल अशून्य हल है, तो r1≠r2,r1,r2≠1
कथन-2 : समीकरणों a1x+b1y+c1z=0,a2x+b2y+c2z=0,a3x+b3y+c3z=0 के केवल अशून्य हल है यदि ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣≠0हल देखेंQuestion 85
यदि A एक m×n कोटि का आव्यूह है, यदि n×m कोटि के आव्यूह L का अस्तित्व इस प्रकार है कि LA=In, तब L को A का बायाँ प्रतिलोम कहा जाता है। इसी प्रकार यदि ये n×m कोटि को आव्यूह R का अस्तित्व इस प्रकार है कि AR=Im, तब R को A दायाँ प्रतिलोम कहा जाता है।
आव्यूह के दाएँ प्रतिलोम ज्ञात करने का उदाहरण है
A=⎡⎢⎣1−11123⎤⎥⎦ हम ले सकते है R=[xyzuvw] तथा AR का हल =I3 अर्थात
⎡⎢⎣1−11123⎤⎥⎦[xyzuvw]=⎡⎢⎣100010001⎤⎥⎦
⇒x−u=1y−v=0z−w=0x+u=0y+v=1z+w=02x+3u=02y+3v=02z+3w=1
अतः इस निकाय के समीकरण असंगत है।
हम कह सकते है कि आव्यूह A के लिए कोई भी दायाँ प्रतिलोम नहीं है
निम्न आव्यूहों में से कौन सा आव्यूह ⎡⎢⎣1−11123⎤⎥⎦ का बायाँ प्रतिलोम नहीं है हल देखेंQuestion 86
यदि A एक m×n कोटि का आव्यूह है, यदि n×m कोटि के आव्यूह L का अस्तित्व इस प्रकार है कि LA=In, तब L को A का बायाँ प्रतिलोम कहा जाता है। इसी प्रकार यदि ये n×m कोटि को आव्यूह R का अस्तित्व इस प्रकार है कि AR=Im, तब R को A दायाँ प्रतिलोम कहा जाता है।
आव्यूह के दाएँ प्रतिलोम ज्ञात करने का उदाहरण है
A=⎡⎢⎣1−11123⎤⎥⎦ हम ले सकते है R=[xyzuvw] तथा AR का हल =I3 अर्थात
⎡⎢⎣1−11123⎤⎥⎦[xyzuvw]=⎡⎢⎣100010001⎤⎥⎦
⇒x−u=1y−v=0z−w=0x+u=0y+v=1z+w=02x+3u=02y+3v=02z+3w=1
अतः इस निकाय के समीकरण असंगत है।
हम कह सकते है कि आव्यूह A के लिए कोई भी दायाँ प्रतिलोम नहीं है
निम्न आव्यूहों में से कौन सा आव्यूह ⎡⎢⎣1−11123⎤⎥⎦ का बायाँ प्रतिलोम नहीं है हल देखेंQuestion 87
यदि A एक m×n कोटि का आव्यूह है, यदि n×m कोटि के आव्यूह L का अस्तित्व इस प्रकार है कि LA=In, तब L को A का बायाँ प्रतिलोम कहा जाता है। इसी प्रकार यदि ये n×m कोटि को आव्यूह R का अस्तित्व इस प्रकार है कि AR=Im, तब R को A दायाँ प्रतिलोम कहा जाता है।
आव्यूह के दाएँ प्रतिलोम ज्ञात करने का उदाहरण है
A=⎡⎢⎣1−11123⎤⎥⎦ हम ले सकते है R=[xyzuvw] तथा AR का हल =I3 अर्थात
⎡⎢⎣1−11123⎤⎥⎦[xyzuvw]=⎡⎢⎣100010001⎤⎥⎦
⇒x−u=1y−v=0z−w=0x+u=0y+v=1z+w=02x+3u=02y+3v=02z+3w=1
अतः इस निकाय के समीकरण असंगत है।
हम कह सकते है कि आव्यूह A के लिए कोई भी दायाँ प्रतिलोम नहीं है
निम्न आव्यूहों में से कौन सा आव्यूह ⎡⎢⎣1−11123⎤⎥⎦ का बायाँ प्रतिलोम नहीं है हल देखेंQuestion 88
यदि A एक m×n कोटि का आव्यूह है, यदि n×m कोटि के आव्यूह L का अस्तित्व इस प्रकार है कि LA=In, तब L को A का बायाँ प्रतिलोम कहा जाता है। इसी प्रकार यदि ये n×m कोटि को आव्यूह R का अस्तित्व इस प्रकार है कि AR=Im, तब R को A दायाँ प्रतिलोम कहा जाता है।
आव्यूह के दाएँ प्रतिलोम ज्ञात करने का उदाहरण है
A=⎡⎢⎣1−11123⎤⎥⎦ हम ले सकते है R=[xyzuvw] तथा AR का हल =I3 अर्थात
⎡⎢⎣1−11123⎤⎥⎦[xyzuvw]=⎡⎢⎣100010001⎤⎥⎦
⇒x−u=1y−v=0z−w=0x+u=0y+v=1z+w=02x+3u=02y+3v=02z+3w=1
अतः इस निकाय के समीकरण असंगत है।
हम कह सकते है कि आव्यूह A के लिए कोई भी दायाँ प्रतिलोम नहीं है
आव्यूह [1−122−11] के कितने दाएँ प्रतिलोम आव्यूह है हल देखेंQuestion 89
यदि A एक m×n कोटि का आव्यूह है, यदि n×m कोटि के आव्यूह L का अस्तित्व इस प्रकार है कि LA=In, तब L को A का बायाँ प्रतिलोम कहा जाता है। इसी प्रकार यदि ये n×m कोटि को आव्यूह R का अस्तित्व इस प्रकार है कि AR=Im, तब R को A दायाँ प्रतिलोम कहा जाता है।
आव्यूह के दाएँ प्रतिलोम ज्ञात करने का उदाहरण है
A=⎡⎢⎣1−11123⎤⎥⎦ हम ले सकते है R=[xyzuvw] तथा AR का हल =I3 अर्थात
⎡⎢⎣1−11123⎤⎥⎦[xyzuvw]=⎡⎢⎣100010001⎤⎥⎦
⇒x−u=1y−v=0z−w=0x+u=0y+v=1z+w=02x+3u=02y+3v=02z+3w=1
अतः इस निकाय के समीकरण असंगत है।
हम कह सकते है कि आव्यूह A के लिए कोई भी दायाँ प्रतिलोम नहीं है
निम्न आव्यूहों में से कौन सा आव्यूह ⎡⎢⎣1−11123⎤⎥⎦ का बायाँ प्रतिलोम नहीं है हल देखेंQuestion 90
यदि A एक m×n कोटि का आव्यूह है, यदि n×m कोटि के आव्यूह L का अस्तित्व इस प्रकार है कि LA=In, तब L को A का बायाँ प्रतिलोम कहा जाता है। इसी प्रकार यदि ये n×m कोटि को आव्यूह R का अस्तित्व इस प्रकार है कि AR=Im, तब R को A दायाँ प्रतिलोम कहा जाता है।
आव्यूह के दाएँ प्रतिलोम ज्ञात करने का उदाहरण है
A=⎡⎢⎣1−11123⎤⎥⎦ हम ले सकते है R=[xyzuvw] तथा AR का हल =I3 अर्थात
⎡⎢⎣1−11123⎤⎥⎦[xyzuvw]=⎡⎢⎣100010001⎤⎥⎦
⇒x−u=1y−v=0z−w=0x+u=0y+v=1z+w=02x+3u=02y+3v=02z+3w=1
अतः इस निकाय के समीकरण असंगत है।
हम कह सकते है कि आव्यूह A के लिए कोई भी दायाँ प्रतिलोम नहीं है
निम्न आव्यूहों में से कौन सा आव्यूह ⎡⎢⎣1−11123⎤⎥⎦ का बायाँ प्रतिलोम नहीं है हल देखेंQuestion 97
माना A=[aij] एक n×n कोटि का आव्यूह है A का अभिलाक्षणिक आव्यूह A−λI है, जहाँ λ अदिश है तथा I एक तत्समक आव्यूह है λ के रूप में सारणिक |A−λI|,n घात का अशून्य बहुपद है जिसे A का अभिलाक्षणिक बुहपद कहा जाता है, |A−λI|=0 को आव्यूह A का अभिलाक्षणिक समीकरण कहते है। इसके मुलो को अभिलाक्षणिक मूल या गुप्त मूल या आइगन मान कहते है आव्यूह A को सभी आइगन मानों का समुच्चय A का स्पेक्ट्रम कहलाता है। आव्यूह A के आइगन मानों के गुणज सारणिक A के बराबर है।
आव्यूह A=⎡⎢⎣102012120⎤⎥⎦ के अभिलाक्षणिक मूल है हल देखेंQuestion 98
माना A=[aij] एक n×n कोटि का आव्यूह है A का अभिलाक्षणिक आव्यूह A−λI है, जहाँ λ अदिश है तथा I एक तत्समक आव्यूह है λ के रूप में सारणिक |A−λI|,n घात का अशून्य बहुपद है जिसे A का अभिलाक्षणिक बुहपद कहा जाता है, |A−λI|=0 को आव्यूह A का अभिलाक्षणिक समीकरण कहते है। इसके मुलो को अभिलाक्षणिक मूल या गुप्त मूल या आइगन मान कहते है आव्यूह A को सभी आइगन मानों का समुच्चय A का स्पेक्ट्रम कहलाता है। आव्यूह A के आइगन मानों के गुणज सारणिक A के बराबर है।
आव्यूह A=⎡⎢⎣102012120⎤⎥⎦ के अभिलाक्षणिक मूल है हल देखेंQuestion 99
माना A=[aij] एक n×n कोटि का आव्यूह है A का अभिलाक्षणिक आव्यूह A−λI है, जहाँ λ अदिश है तथा I एक तत्समक आव्यूह है λ के रूप में सारणिक |A−λI|,n घात का अशून्य बहुपद है जिसे A का अभिलाक्षणिक बुहपद कहा जाता है, |A−λI|=0 को आव्यूह A का अभिलाक्षणिक समीकरण कहते है। इसके मुलो को अभिलाक्षणिक मूल या गुप्त मूल या आइगन मान कहते है आव्यूह A को सभी आइगन मानों का समुच्चय A का स्पेक्ट्रम कहलाता है। आव्यूह A के आइगन मानों के गुणज सारणिक A के बराबर है।
आव्यूह A=⎡⎢⎣1−333−536−64⎤⎥⎦ के दिए गए मान हैहल देखेंQuestion 100
माना A=[aij] एक n×n कोटि का आव्यूह है A का अभिलाक्षणिक आव्यूह A−λI है, जहाँ λ अदिश है तथा I एक तत्समक आव्यूह है λ के रूप में सारणिक |A−λI|,n घात का अशून्य बहुपद है जिसे A का अभिलाक्षणिक बुहपद कहा जाता है, |A−λI|=0 को आव्यूह A का अभिलाक्षणिक समीकरण कहते है। इसके मुलो को अभिलाक्षणिक मूल या गुप्त मूल या आइगन मान कहते है आव्यूह A को सभी आइगन मानों का समुच्चय A का स्पेक्ट्रम कहलाता है। आव्यूह A के आइगन मानों के गुणज सारणिक A के बराबर है।
आव्यूह A=⎡⎢⎣1−333−536−64⎤⎥⎦ के दिए गए मान हैहल देखेंQuestion 101
माना A=[aij] एक n×n कोटि का आव्यूह है A का अभिलाक्षणिक आव्यूह A−λI है, जहाँ λ अदिश है तथा I एक तत्समक आव्यूह है λ के रूप में सारणिक |A−λI|,n घात का अशून्य बहुपद है जिसे A का अभिलाक्षणिक बुहपद कहा जाता है, |A−λI|=0 को आव्यूह A का अभिलाक्षणिक समीकरण कहते है। इसके मुलो को अभिलाक्षणिक मूल या गुप्त मूल या आइगन मान कहते है आव्यूह A को सभी आइगन मानों का समुच्चय A का स्पेक्ट्रम कहलाता है। आव्यूह A के आइगन मानों के गुणज सारणिक A के बराबर है।
निम्न में से कौन सा कथन सत्य है यदि A,n×n कोटि का कोई आव्यूह हो तथा λ,A का अभिलाक्षणिक मूल हो, तो हल देखेंQuestion 102
माना A=[aij] एक n×n कोटि का आव्यूह है A का अभिलाक्षणिक आव्यूह A−λI है, जहाँ λ अदिश है तथा I एक तत्समक आव्यूह है λ के रूप में सारणिक |A−λI|,n घात का अशून्य बहुपद है जिसे A का अभिलाक्षणिक बुहपद कहा जाता है, |A−λI|=0 को आव्यूह A का अभिलाक्षणिक समीकरण कहते है। इसके मुलो को अभिलाक्षणिक मूल या गुप्त मूल या आइगन मान कहते है आव्यूह A को सभी आइगन मानों का समुच्चय A का स्पेक्ट्रम कहलाता है। आव्यूह A के आइगन मानों के गुणज सारणिक A के बराबर है।
निम्न में से कौन सा कथन सत्य है यदि A,n×n कोटि का कोई आव्यूह हो तथा λ,A का अभिलाक्षणिक मूल हो, तो हल देखेंQuestion 115
इस खण्ड में कुछ प्रश्न है। प्रत्येक प्रश्न में कॉलम -I में कुछ कथन (A,B, C और D) और कॉलम -II में कुछ कथन (p,q,r,s और t ) है। कॉलम -I का कोई भी कथन कॉलम -II के एक कथन या एक से अधिक कथनो से मेल खाता है। उदाहरण के लिए दिए हुए प्रश्न में यदि कथन B कथनो q और r से मेल खाता है, तो ORS में उस प्रश्न के लिये कथन B के सामने q और r से संबंधित बुलबुलो को काला कीजिए।
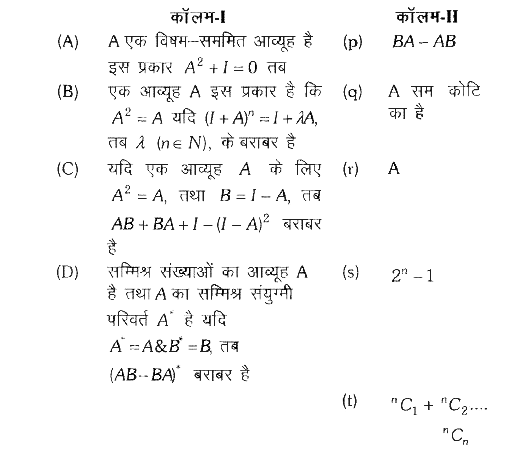 हल देखें
हल देखेंQuestion 116
इस खण्ड में कुछ प्रश्न है। प्रत्येक प्रश्न में कॉलम -I में कुछ कथन (A,B, C और D) और कॉलम -II में कुछ कथन (p,q,r,s और t ) है। कॉलम -I का कोई भी कथन कॉलम -II के एक कथन या एक से अधिक कथनो से मेल खाता है। उदाहरण के लिए दिए हुए प्रश्न में यदि कथन B कथनो q और r से मेल खाता है, तो ORS में उस प्रश्न के लिये कथन B के सामने q और r से संबंधित बुलबुलो को काला कीजिए।
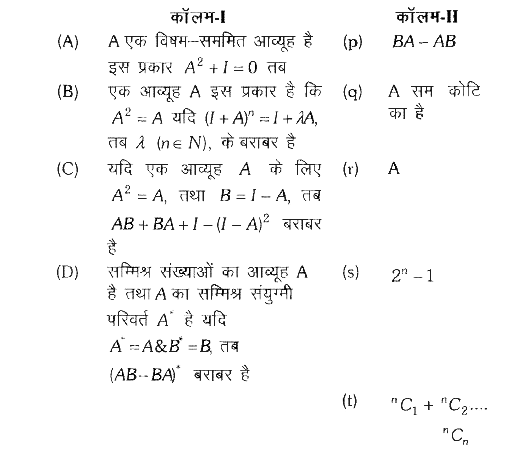 हल देखें
हल देखें
ERRORLESS MATHS (HINDI) सारणिक तथा आव्यूह की सभी प्रश्नावली कक्षा 12 के लिए
- SOLVED MULTIPLE CHOICE QUESTIONS ( आव्यूह के प्रकार, आव्यूह का बीजगणित)
- SOLVED MULTIPLE CHOICE QUESTIONS ( रैखिक समीकरणों का निकाय कुछ विशेष सारणिक, सारणिक का अवकलन तथा समाकलन)
- SOLVED MULTIPLE CHOICE QUESTIONS ( विशेष प्रकार के आव्यूह, परिवर्त आव्यूह सहखण्डज व व्युत्क्रम आव्यूह)
- SOLVED MULTIPLE CHOICE QUESTIONS ( सारणिक व आव्यूह के बीच सम्बन्ध आव्यूह की जाति (रैंक) तथा समीकरणों का हल)
- SOLVED MULTIPLE CHOICE QUESTIONS (उपसारणिक और सहखण्ड, सारणिक गुणन)
- SOLVED MULTIPLE CHOICE QUESTIONS (सारणिक का प्रसार , सारणिक के रूप में समीकरण का हल एवं सारणिक के गुणधर्म)
- EXERCISE
- JEE ADVANCED MORE THAN ONE CORRECT ANSWERS
- JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (COMPREHENSION TYPE QUESTIONS) (PASSAGE-I)
- JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (COMPREHENSION TYPE QUESTIONS) (PASSAGE-II)
- JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (COMPREHENSION TYPE QUESTIONS) (PASSAGE-III)
- JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (COMPREHENSION TYPE QUESTIONS) (PASSAGE-IV)
- JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (COMPREHENSION TYPE QUESTIONS) (PASSAGE-V)
- JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (COMPREHENSION TYPE QUESTIONS) (PASSAGE-VI)
- JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (INTEGER TYPE QUESTIONS)
- JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (MATRIX MATCH TYPE QUESTIONS)
- ILLUSTRATION