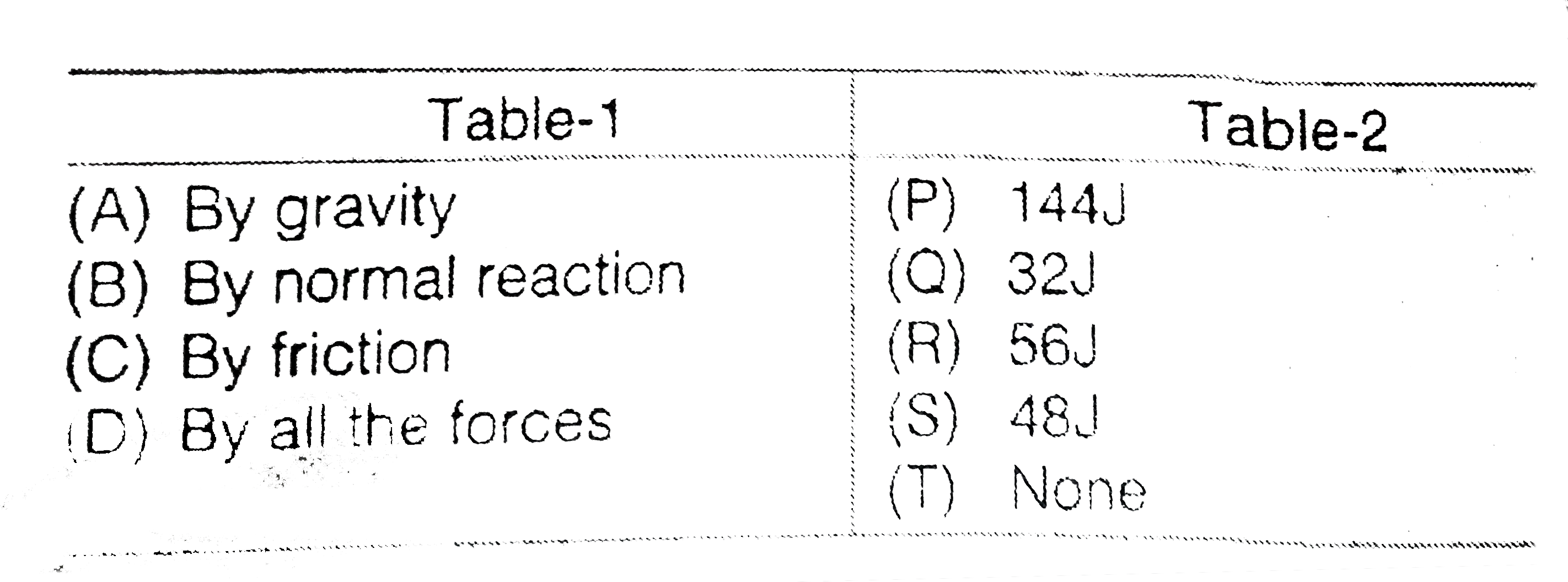A Only One Option is Correct from DC PANDEY ENGLISH WORK, POWER AND ENERGY for Class 11
| Class 11 | PHYSICS |
| Chapter | WORK, POWER AND ENERGY |
| DC PANDEY ENGLISH | A Only One Option is Correct |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
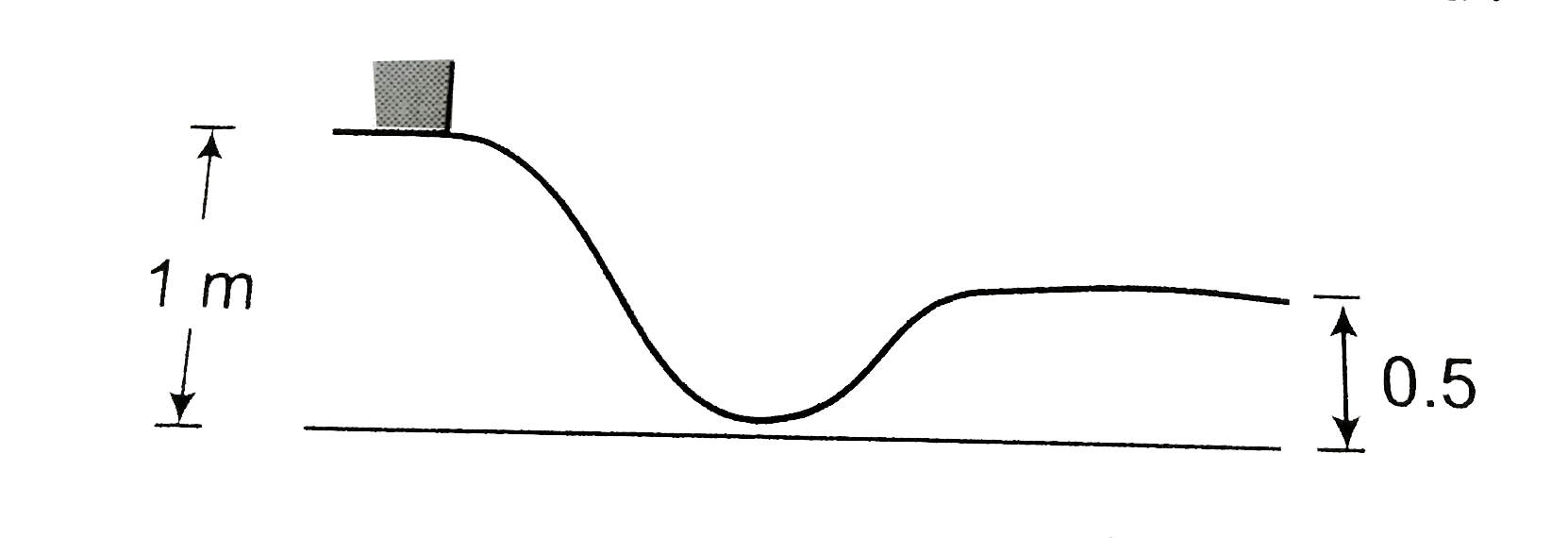
A block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block is released from rest on the track from a point 1.0 m above the horizontal surface, the distance it will move on the rough surface is
 View Solution
View SolutionQuestion 38
A spring and block are placed on a fixed smooth wedge as shown. Following conclusions can be drawn for the block.
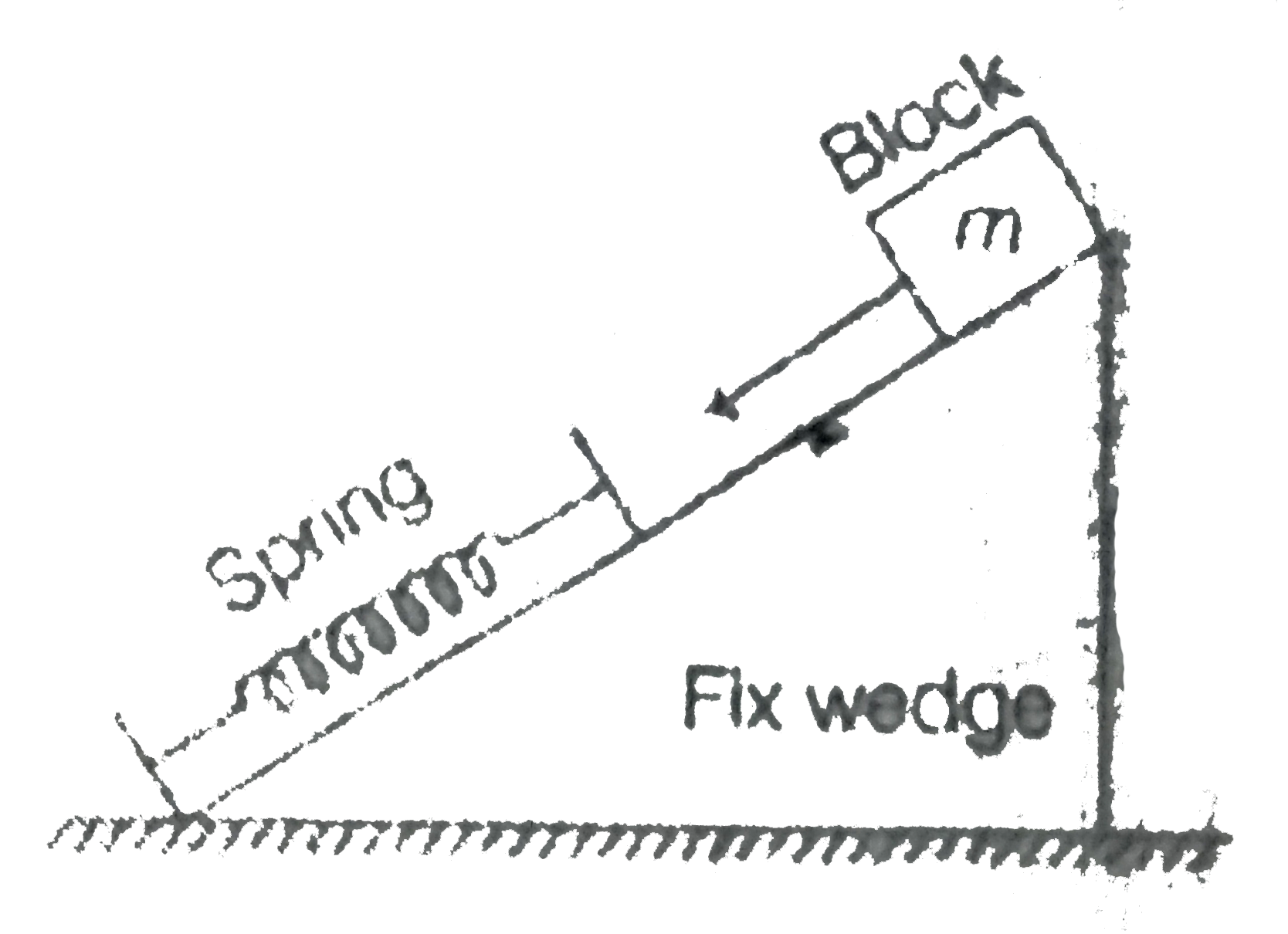
(i) magnitude of its momentum will be maximum when Fnet on block is zero
(ii) its kinetic energy will be maximum when Fnet on block is zero
(iii) kinetic energy of block is maximum when block just touches the spring
(iv) net force on block is maximum when KE = 0
View SolutionQuestion 49
A partical is realeased from the top of two inclined rought surface of height h each. The angle of inclination of the two planes are 30∘ and 60∘ respectively. All other factors (e.g. coefficient of friction , mass of the block etc) are same in both the cases. Let K1andK2 be the kinetic energy of the partical at the bottom of the plane in two cases. Then View SolutionQuestion 52
An object of mass m slides down a hill of arbitrary shape and after travelling a certain horizontal path stops because of friction. The total vertical height descended is h. The friction coefficient is different for different segments for the entire path but is independent of the velocity and direction of motion. The work that a tangerial force must perform to return the object to its initial position along the same path isView SolutionQuestion 53
A block of mass m slides down a rough inclined plane of inclination θ with horizontal with zero initial velocity. The coefficient of friction between the block and the plane is μ with θ>tan−1(μ). Rate of work done by the force of friction at time t is
A.μmg2tsinθ B.mg2t(sinθ−μcosθ) C.μmg2tcosθ(sinθ−μcosθ) D.μmg2tcosθView SolutionQuestion 54
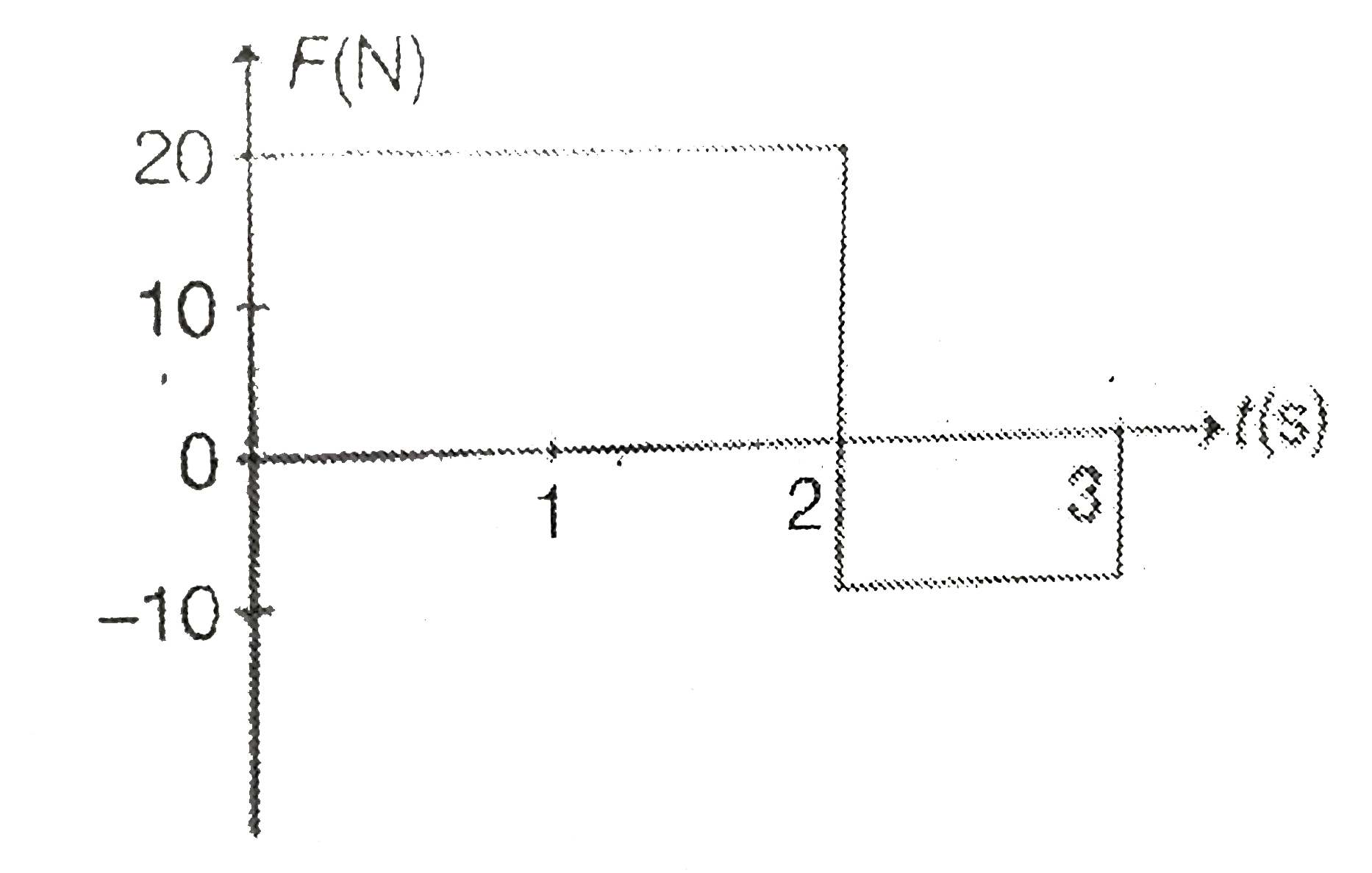
A 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum kinetic energy of the block between x=0 and x=2.0m is
A.2.33 J B.8.67 J C.5.33 J D.6.67 JView SolutionQuestion 56
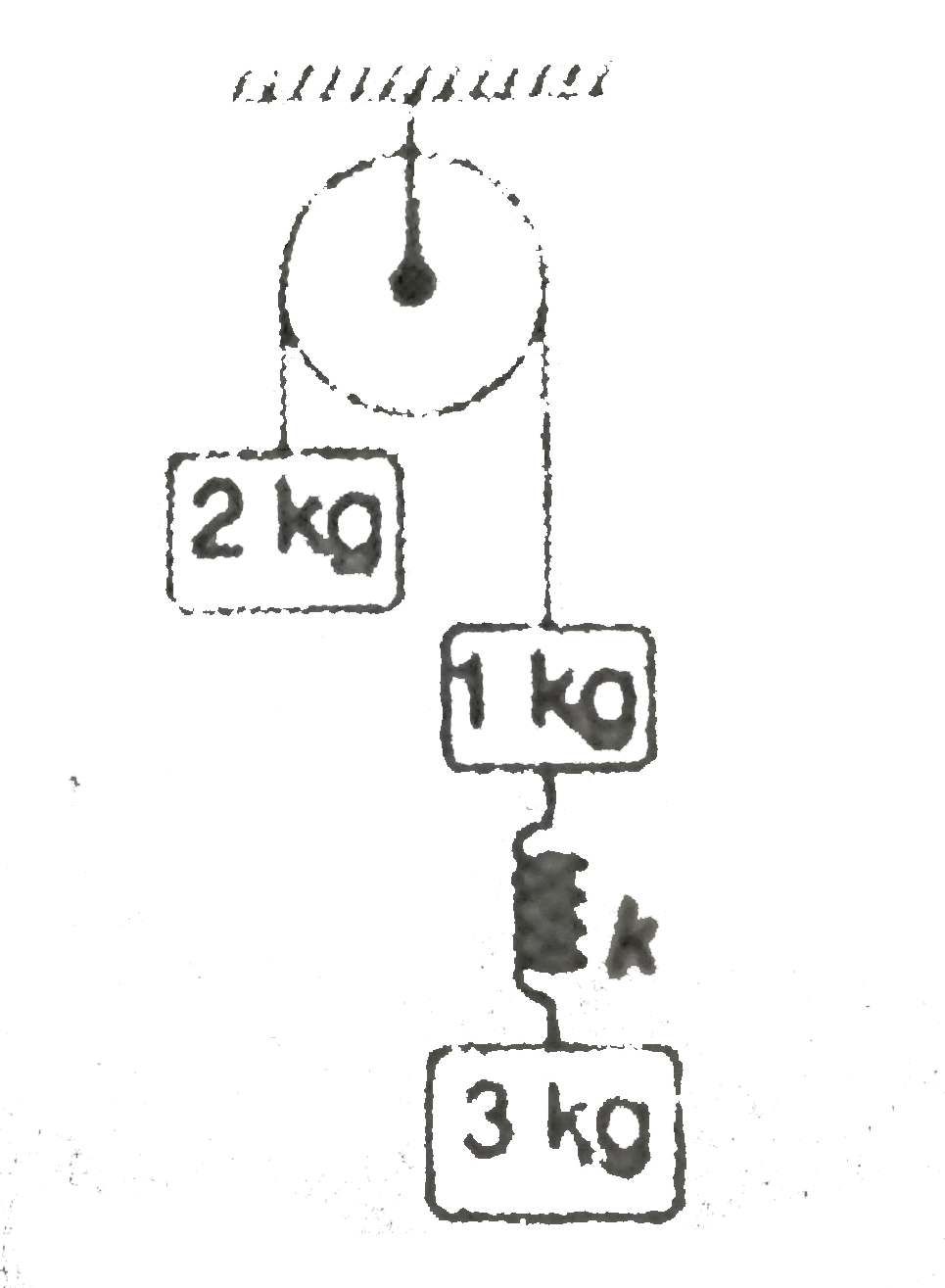
A block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)View SolutionQuestion 57
Two block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?View SolutionQuestion 58
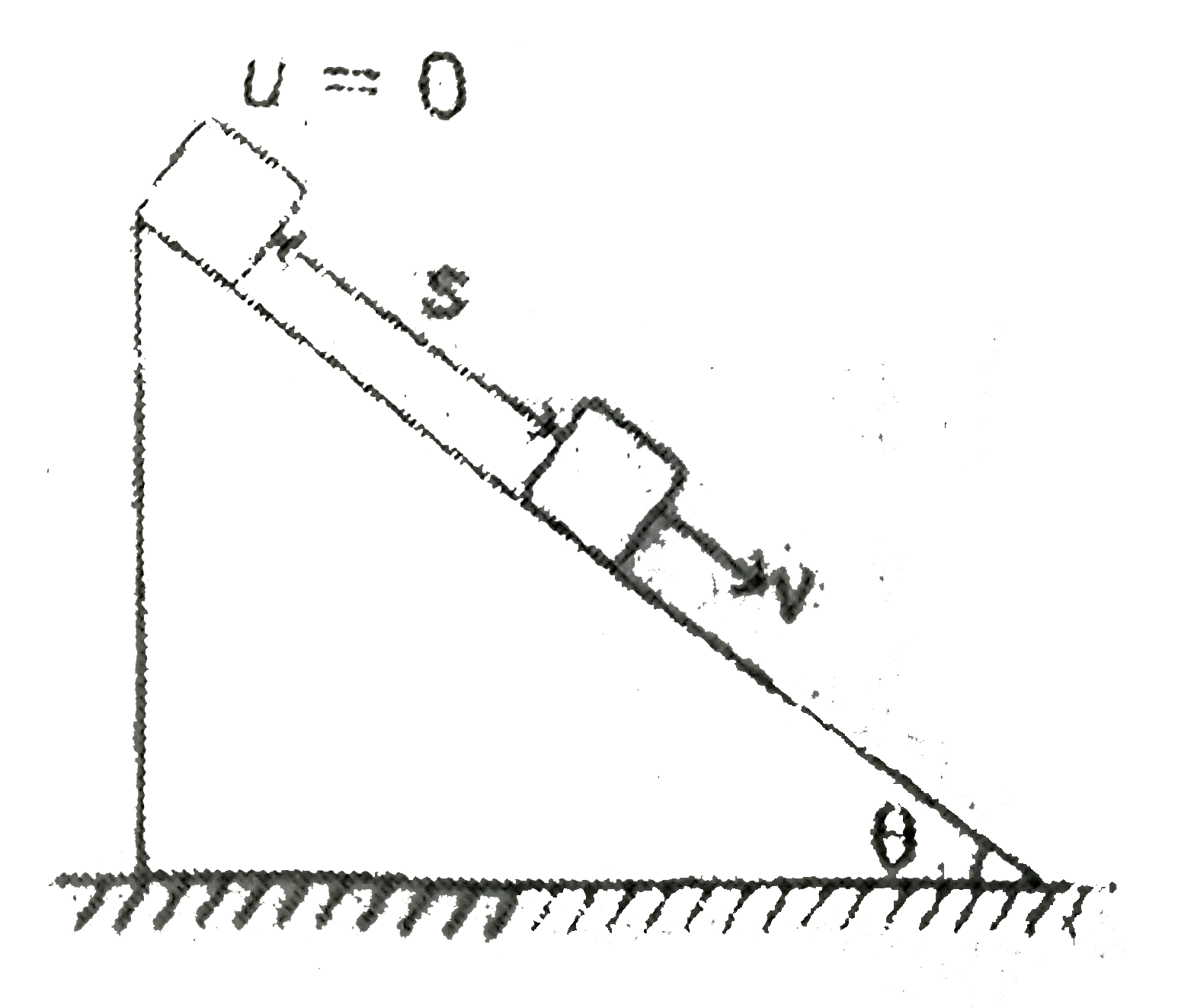
A block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=34. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)
 View Solution
View SolutionQuestion 60
A body of mass 2 kg is moved from a point A to a point B by an external agent in a conservative force field. If the velocity of the body at the points A and B are 5m/s and 3m/s respectively and the work done by the external agent is - 10 J, then the change in potential energy between point A and B is View SolutionQuestion 61
A block of mass m = 0.1 kg is released from a height of 4m on a curved smooth surface. On the horizontal surface, path AB is smooth and path BC offers coefficient of friction μ = 01. If the impact of block with the vertical wall at C be elastic, the total distance covered by the block on the horizontal surface before coming to rest will be (take g=10m/s2)
 View Solution
View SolutionQuestion 63
A block mass m=2kg is moving with velocityv0 towards a mass less unstretched spring of the force constant k=10N/m. Coefficient of friction between the block and the ground is μ=0.2. Find the maximum value of v0 so that after pressing the spring the block does not return back but stops there permanently.
 View Solution
View SolutionQuestion 68
Figure, a block slides along a track from one level to a higher level by moving through an intermediate valley. The track is friction less until the block reaches the higher
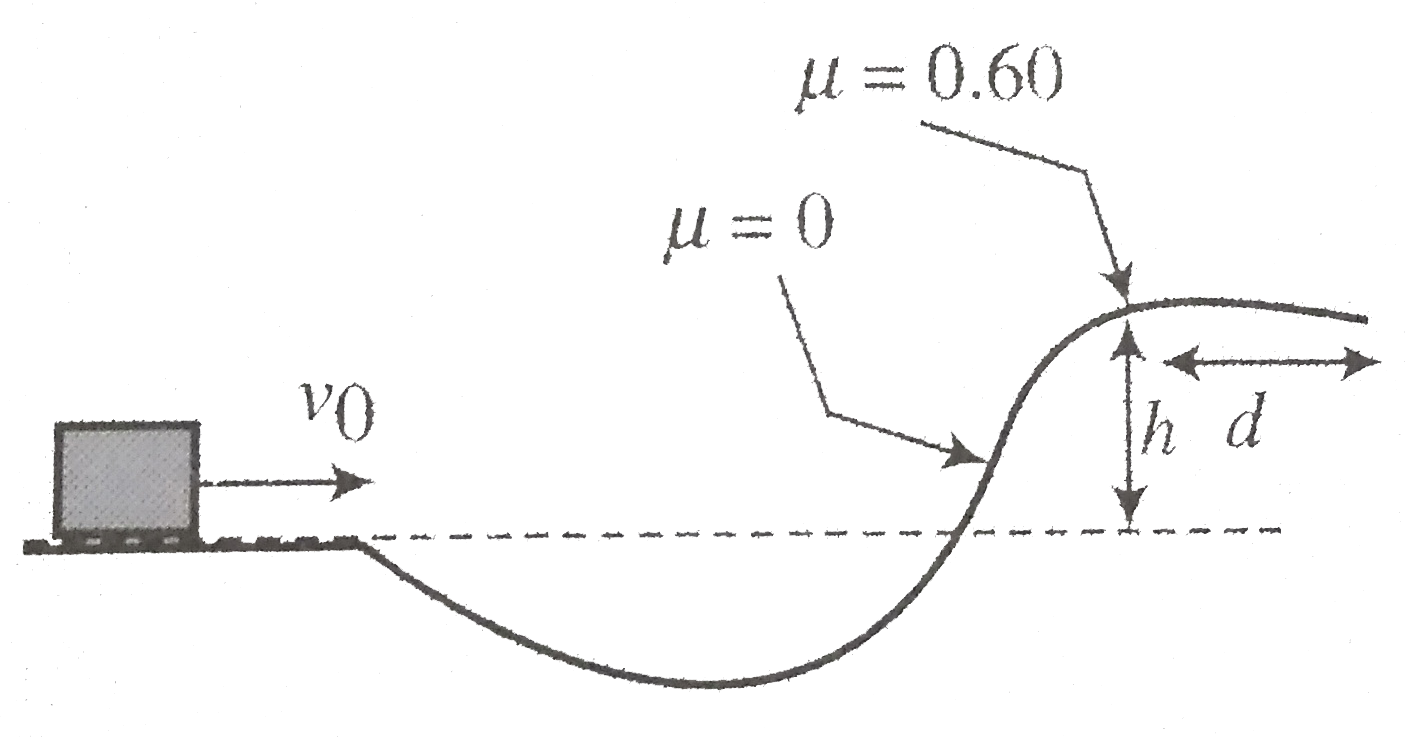 level. Then there is friction force which stops the block at a distance d. The block's initial speed v0 is 6.0ms−1, the height difference h is 1.1m, and the coefficient of kinetic friction μ is 0.60. Find d.View Solution
level. Then there is friction force which stops the block at a distance d. The block's initial speed v0 is 6.0ms−1, the height difference h is 1.1m, and the coefficient of kinetic friction μ is 0.60. Find d.View SolutionQuestion 72
In the figure shown all the surfaces are frictionless and mass of block m=1kg, block and wedge are held initially at rest, now wedge is given a horizontal acceleration of 10m/s2 by applying a force on the wedge so that the block does not slip on the wedge, the work done by normal force in ground frame on the block in √3sec is
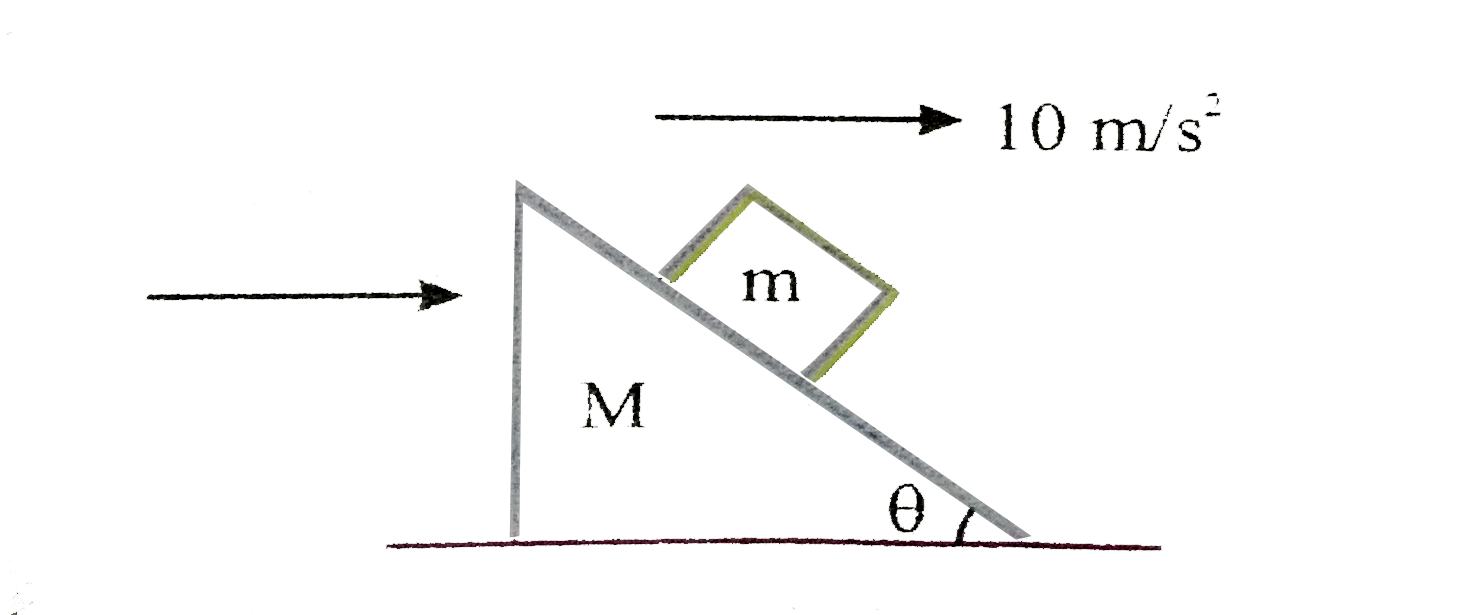 .View Solution
.View SolutionQuestion 77
A block of mass m is attached to a frame by a light spring of force constant k. The frame and block are initially at rest with x=x0, the natural length of the spring. If the frame is given a constant horizontal accelration a0 towards left, determine the maximum velocity of the block relative to the frame (block is free to move inside frame). Ignore any friction.
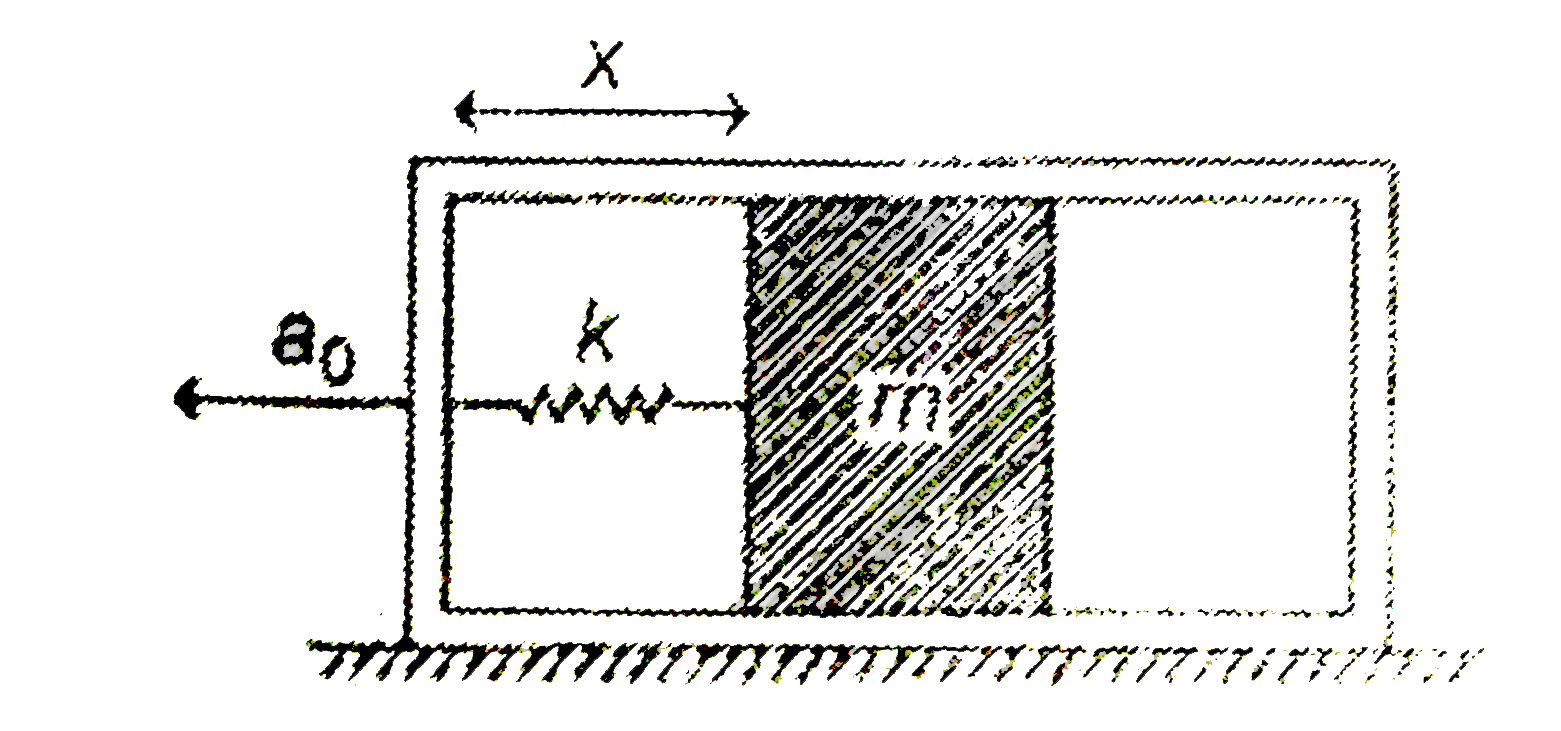 View Solution
View SolutionQuestion 78
Figure shows two small blocks placed on smooth horizontal surface. They start moving from the same line with forces 2F and F respectively acting on the blocks. Their momenta and kinetic energies at the instant of crossing the finishing line as shown in figure are PA,PB and KA,KB. Then choose the correct option.
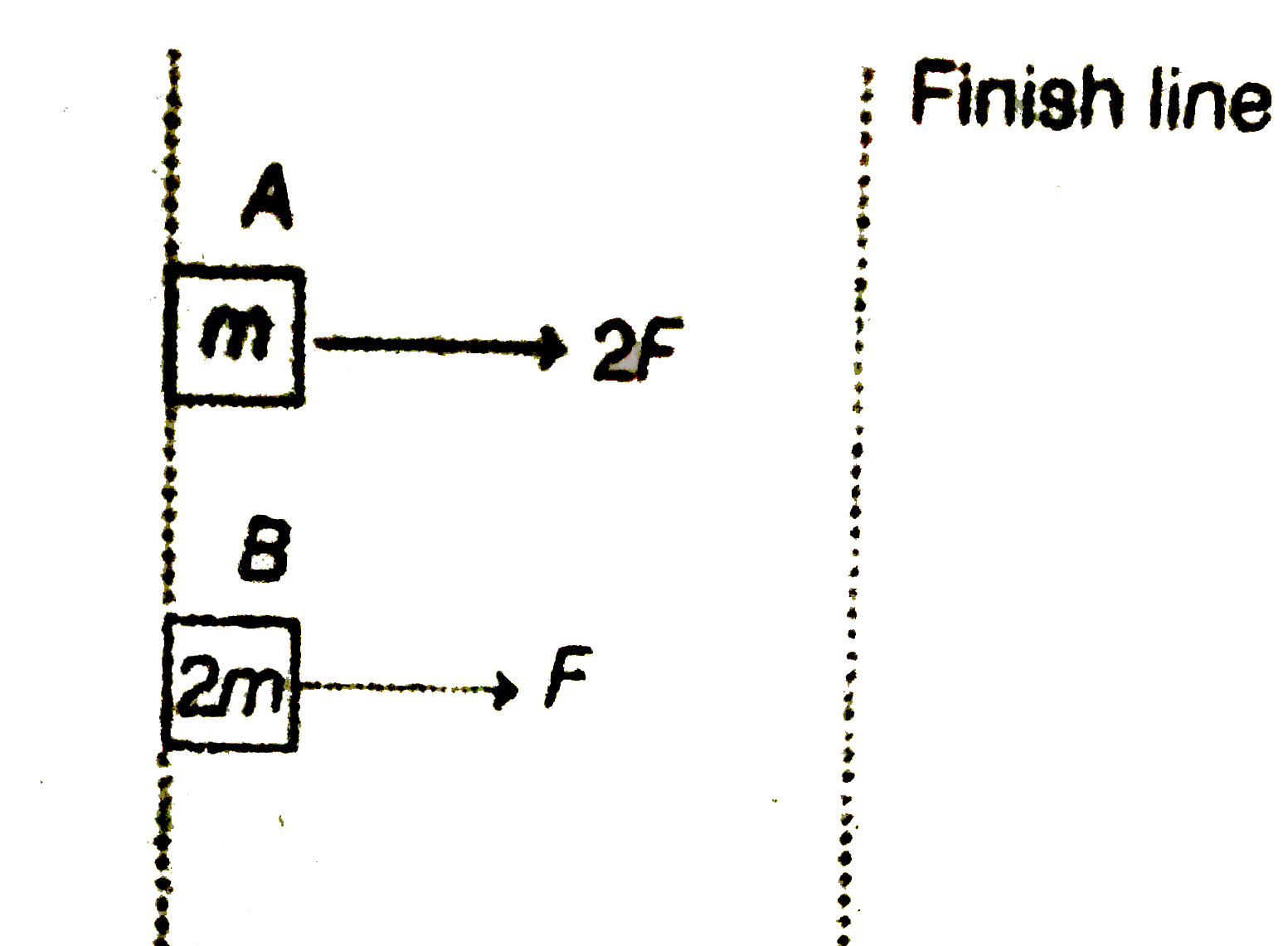 View Solution
View SolutionQuestion 79
Inside a smooth hemispherical cavity, a particle P can slide freely. The block having this cavity is moving with constant acceleration a = g (where g is acceleration due to gravity). The particle is released from the state of rest from the topmost position of the surface of the cavity as shown. The angle θ with the vertical, when the particle will have maximum velocity with respect to the block is
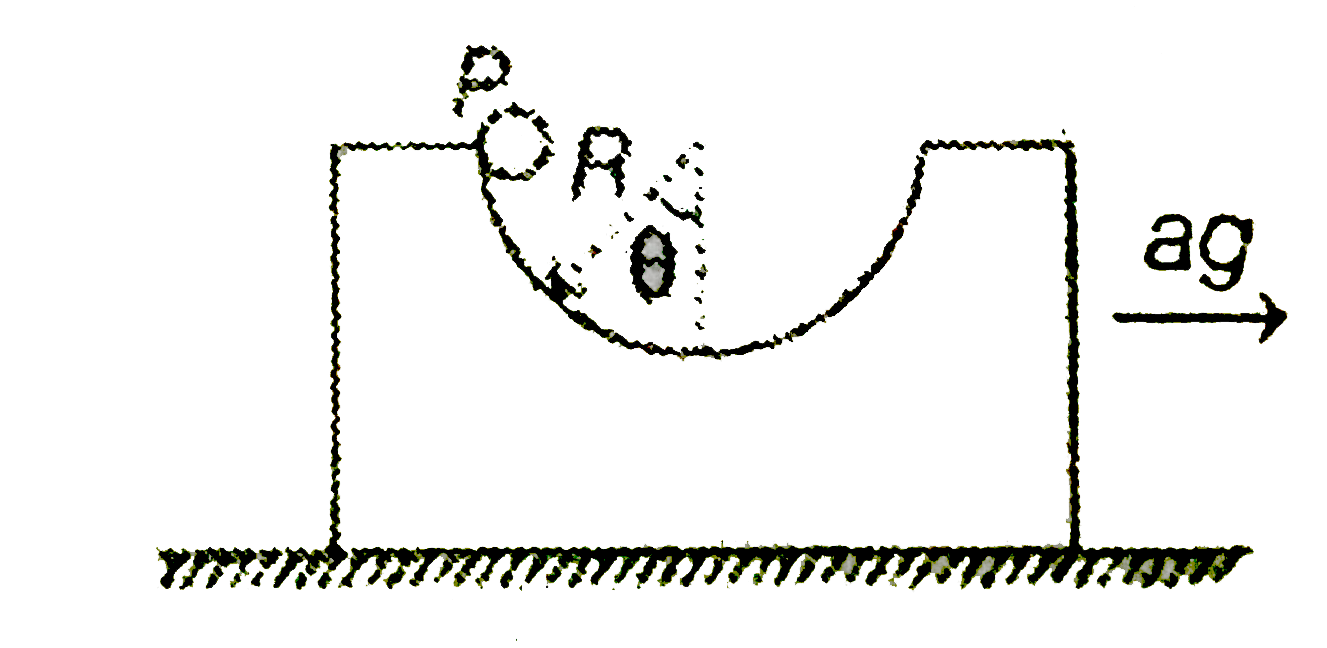 View Solution
View SolutionQuestion 80
A block of mass M slides along a horizontal table with speed v0. At x=0, it hits a spring with spring constant k and begins to experience a friction force. The coefficient of friction is variable and is given by μ=bx, where b is a positive constant. Find the loss in mechanical energy when the block has first come momentarily to rest.
 .View Solution
.View SolutionQuestion 92
A smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
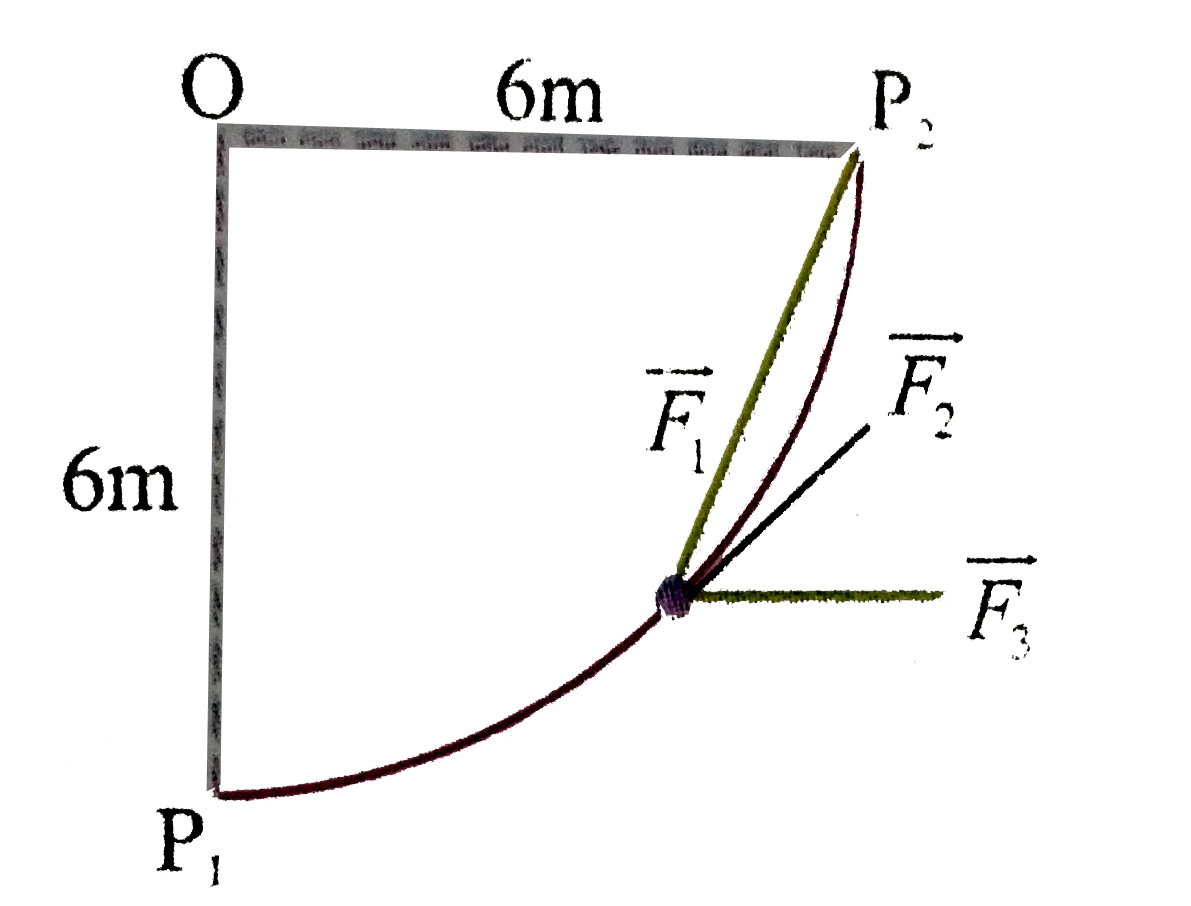 .View Solution
.View SolutionQuestion 104
A bead slides on a fixed frictionless wire bent into a horizontal semicircle of radius R0 as shown in figure. In addition to any normal forces exerted by the wire, the bead is subjected to an external force that points directly away from origin and depends on distance r from the origin according to the formula F=F0(rR0)2ˆr
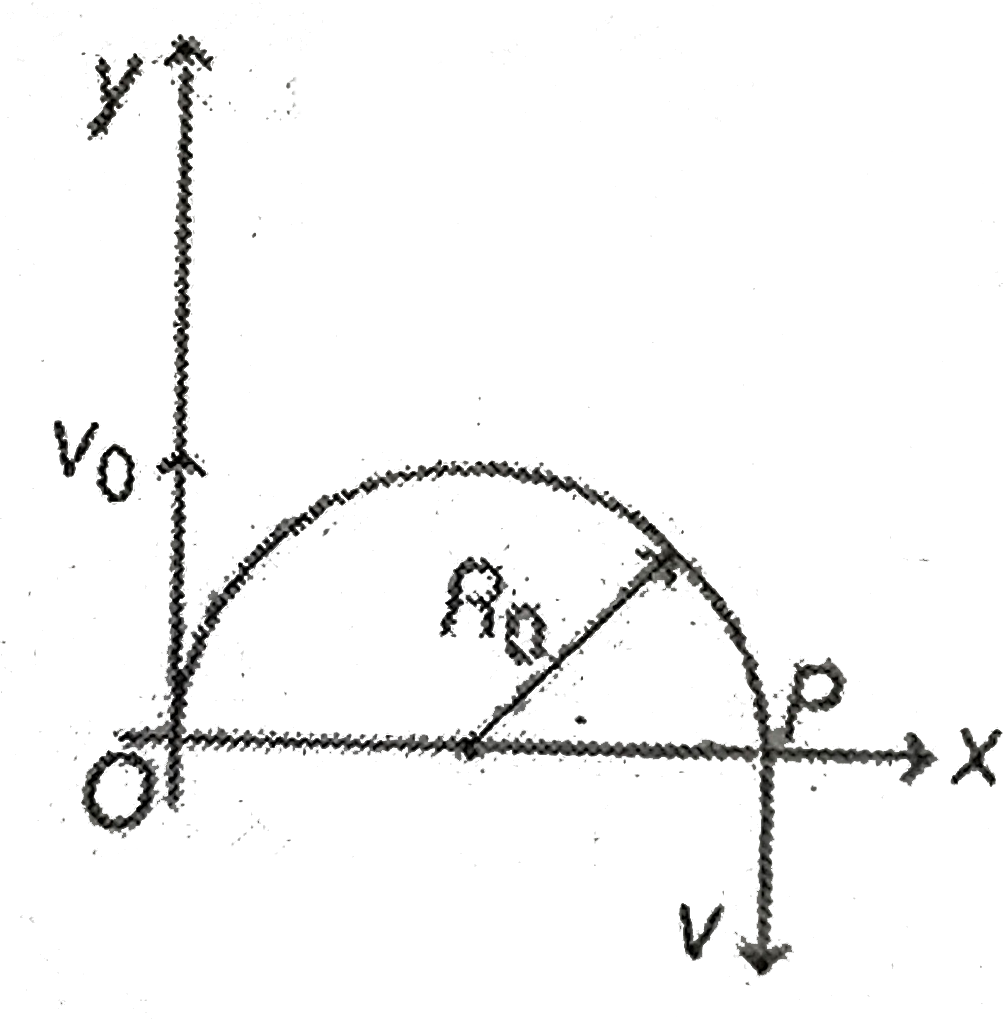 View Solution
View SolutionQuestion 106
In the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.
 View Solution
View SolutionQuestion 116
In a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium distance is given byView SolutionQuestion 117
In a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium is View SolutionQuestion 118
In a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity is View SolutionQuestion 119
In a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
If the total energy of the particle is E=−3B216A, and it is known that the motion is radial only then the velocity is zero at View SolutionQuestion 120
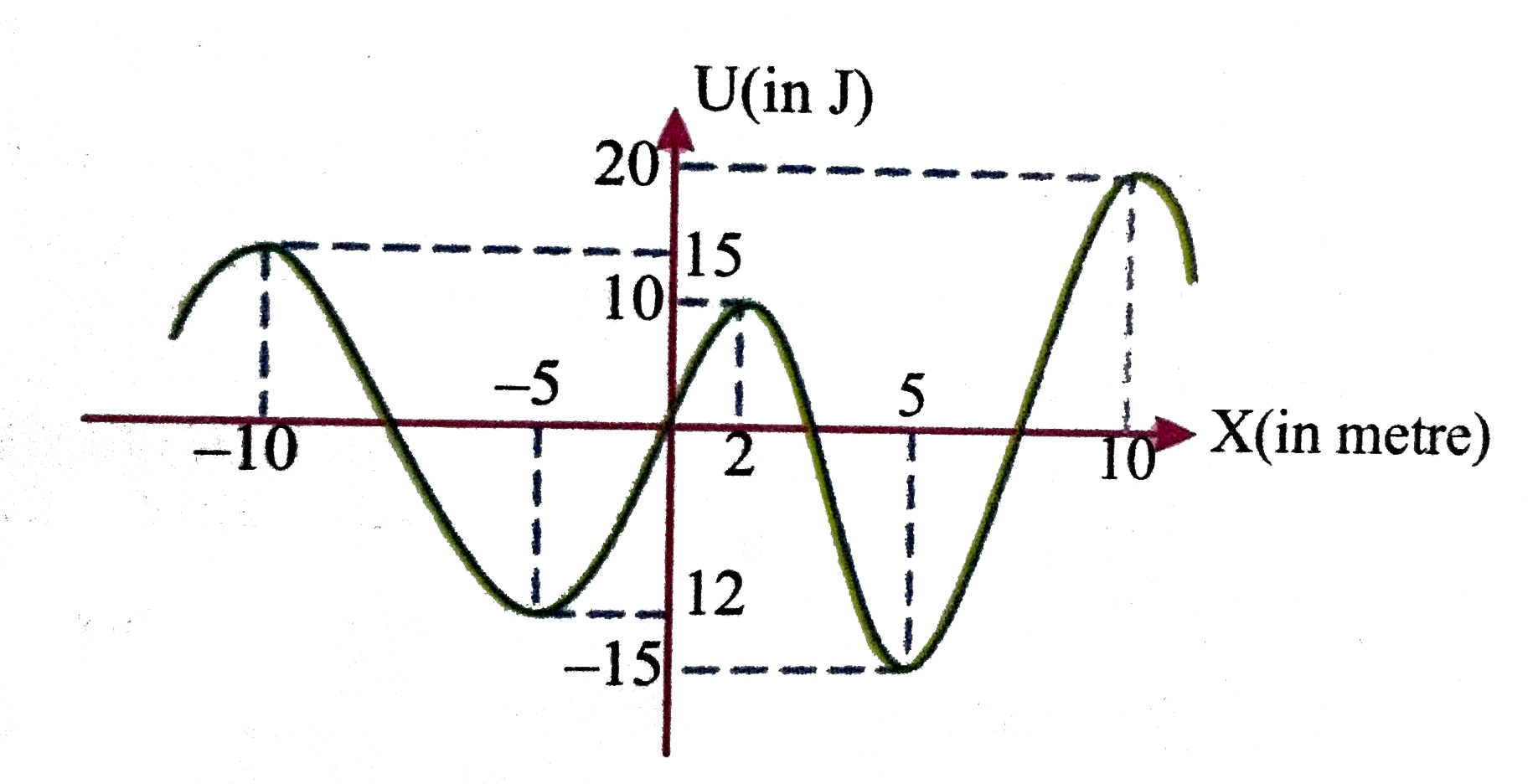
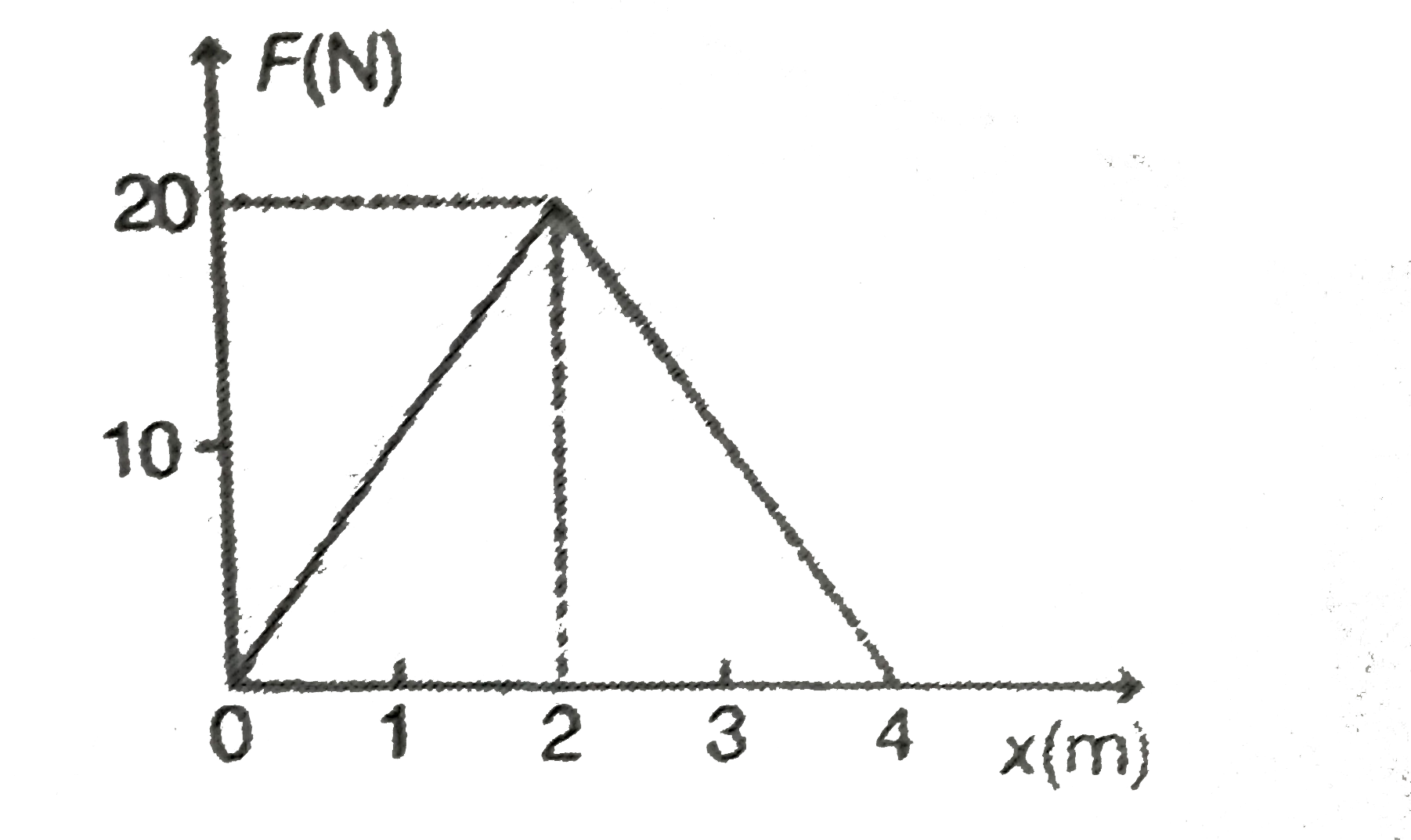
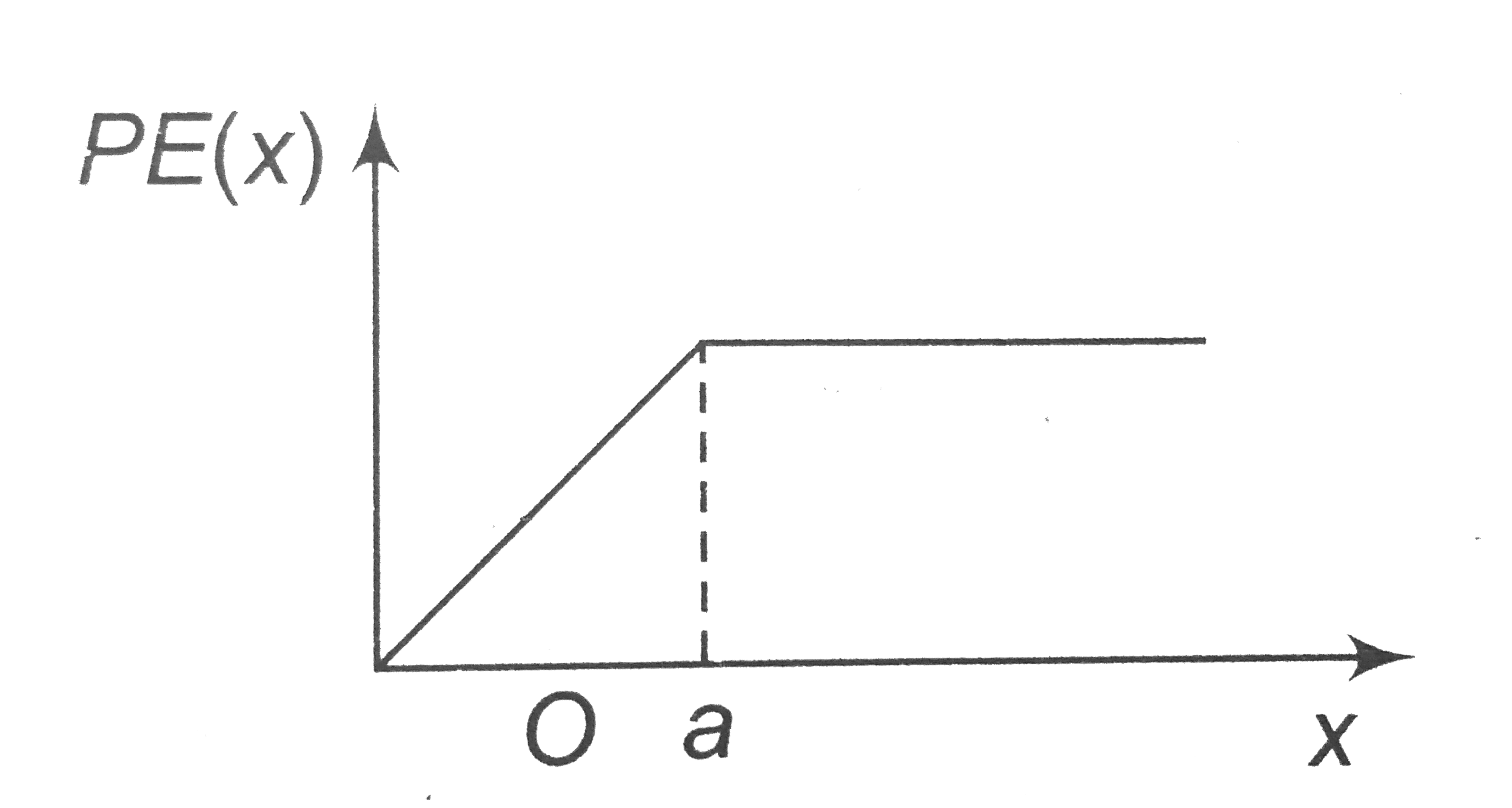
In the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
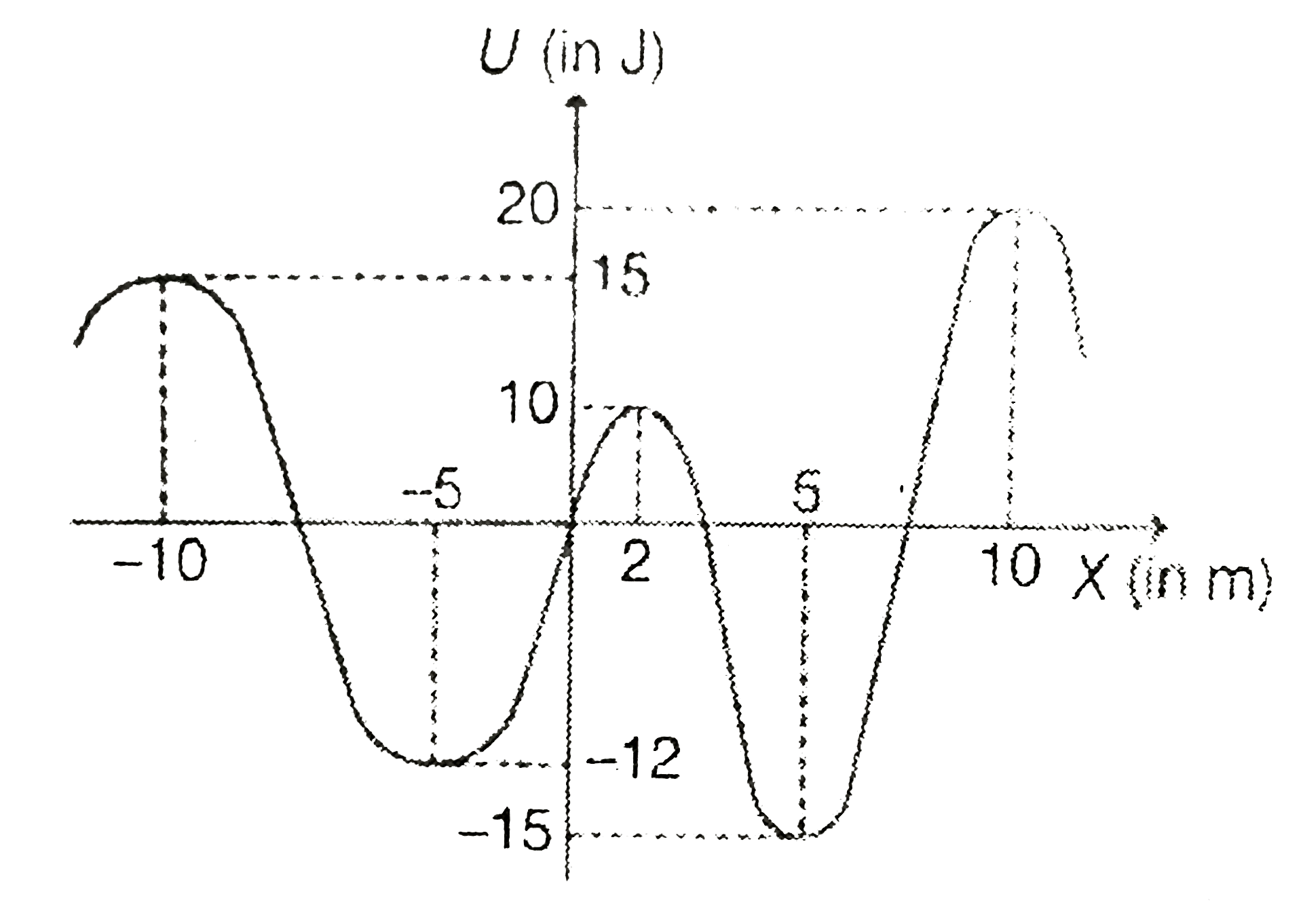
If the particle is released at the origin, then
(A)it will move towards positive x-axis
(B)it will move towards negative x-axis
(C)it will remain stationary at the origin
(D)Either of (a) or (b)View SolutionQuestion 121
In the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
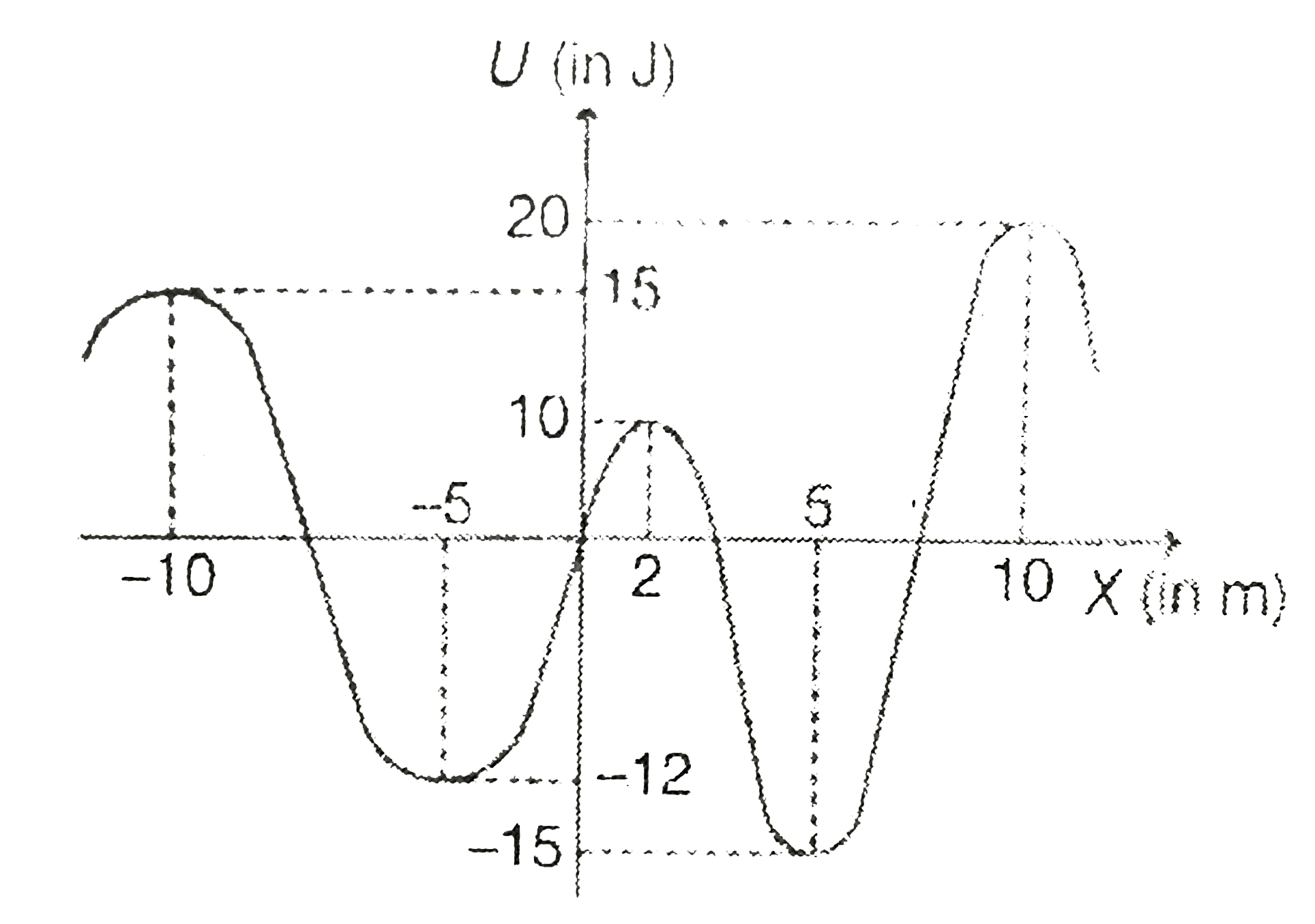
If the particle is released at x=2+Δ where Δ→0 (it is positive), then its maximum speed in subsequent motion will beView SolutionQuestion 123
A block of mass 10 kg is put gently on a belt-conveyor system of infinite length at t = 0, which is moving with constant speed 20m/sec towards right at all time.
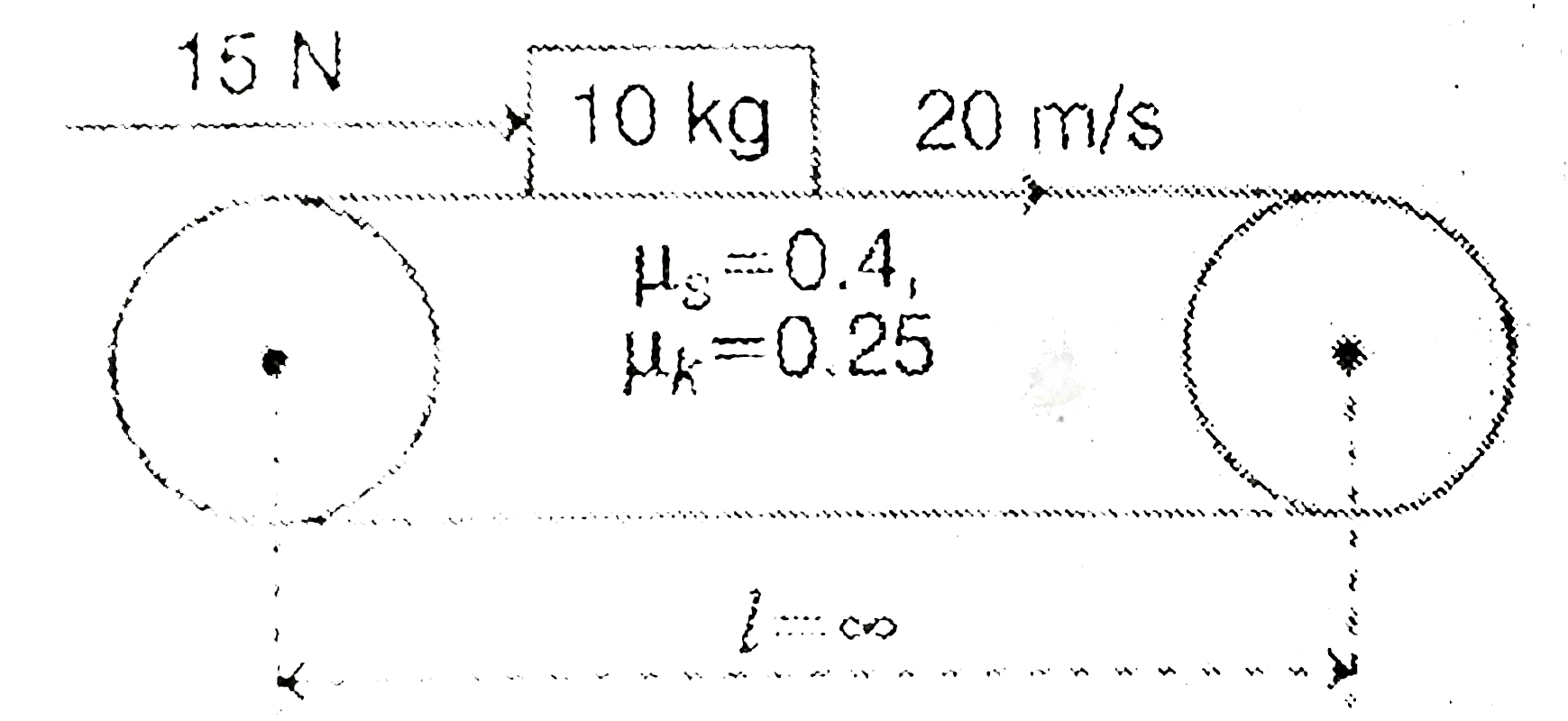
A constant force of magnitude 15 N is applied on the block continuously during its motion.
The nature of friction acting on the block of mass 10 kg during its motion is View SolutionQuestion 124
A block of mass 10 kg is put gently on a belt-conveyor system of infinite length at t = 0, which is moving with constant speed 20m/sec towards right at all time.

A constant force of magnitude 15 N is applied on the block continuously during its motion.
Work done by the kinetic friction on the block of mass 10 kg is View SolutionQuestion 125
A block of mass 10 kg is put gently on a belt-conveyor system of infinite length at t = 0, which is moving with constant speed 20m/sec towards right at all time.
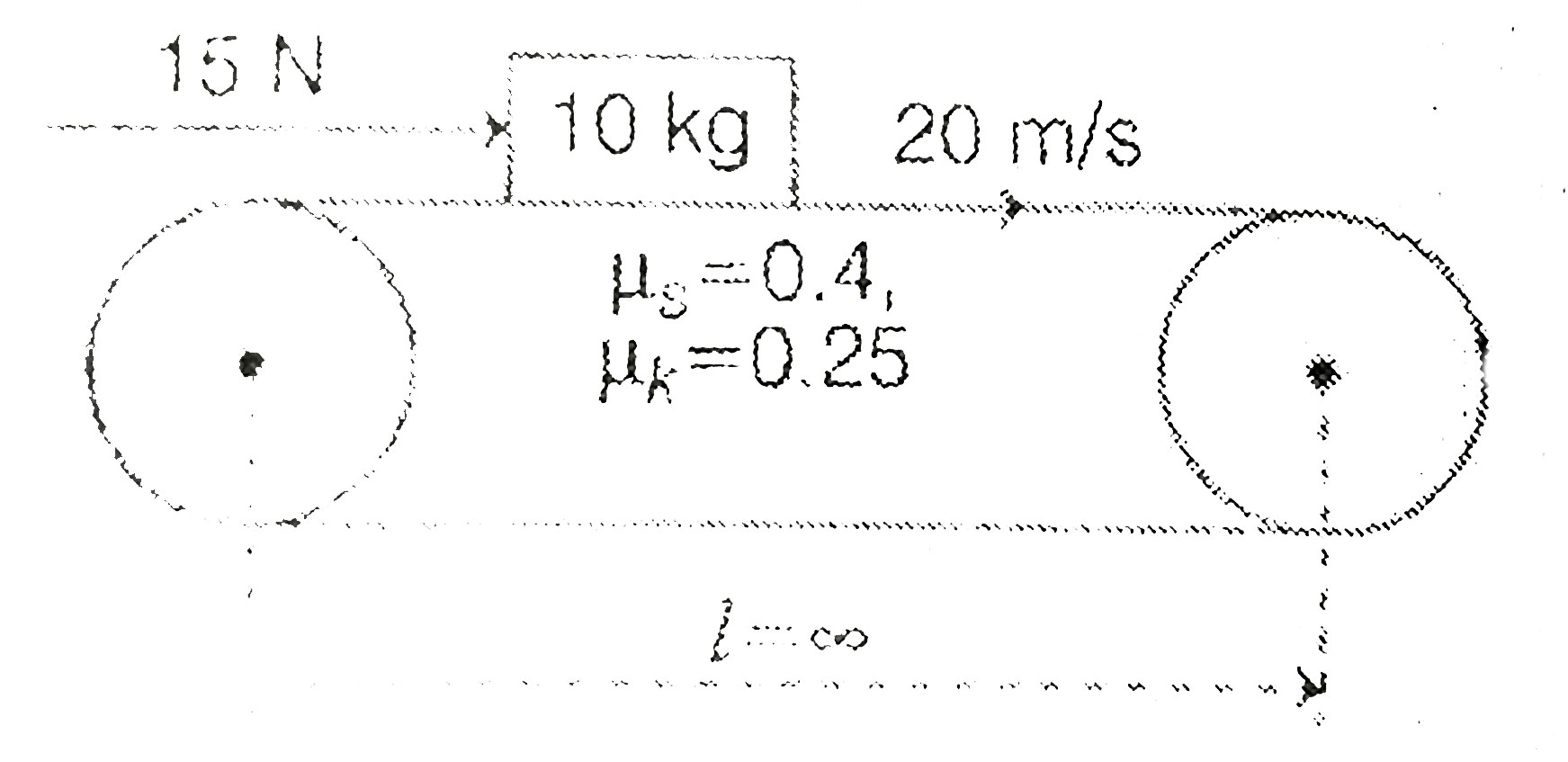
A constant force of magnitude 15 N is applied on the block continuously during its motion.
The magnitude of acceleration of the block of mass 10 kg at t = 6s is View SolutionQuestion 134
A block A of mass m kg lies on a block B of mass m kg. B in turn lies on smooth horizontal plane. The coefficient of friction between A and B is μ. Both the blocks are initially at rest. A horizontal force F is applied to lower block B at t = 0 till the lower block B undergoes a displacement of magnitude L. Match the statements in Table-1 with the results in Table-2.
 View Solution
View SolutionQuestion 135
A block of mass m lies on a wedge of mass M. The wedge in turn lies on smooth horizontal surface. Friction is absent everywhere. The wedge block system is released from rest. All situations given in Table-1 are tol be estimated in the duration the block undergoes a vertical displacement 'h' starting from rest. Match the statement in Table-1 with the results in Table-2 ltbgt View Solution
View SolutionQuestion 136
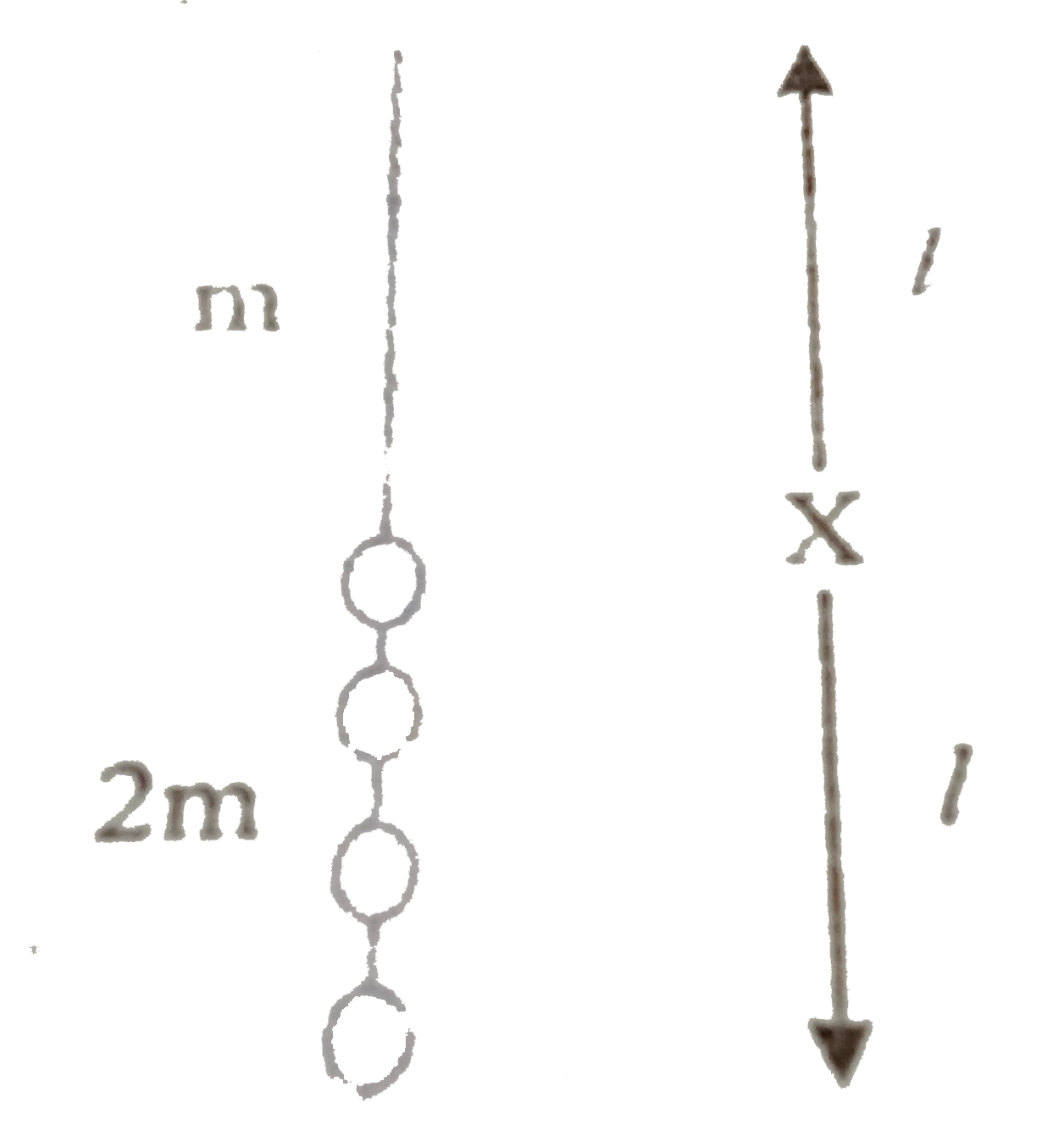
A 4kg block is on a smooth horizontal table. The block is connected to a second block of mass 1kg by a massless flexible taut cord that passes over a frictionless pulley. The 1kg block is 1m above the floor. The two block are released from rest. With what speed does the 1kg block hit the ground?
 . View Solution
. View SolutionQuestion 140
A particle of mass 1 g executes an oscillatory motion on the concave surface of a spherical dish of radius 2m placed on a horizontal plane, Figure . If the motion of the particle begins from a point on the disc at a height of 1 cm. from the horizontal plane and coefficient of friction is 0.01 , find the total distance covered by the particle before coming to rest.
 View Solution
View SolutionQuestion 141
An ideal massles spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless plane inclined at 30∘ to the horizontal. A 10 kg block M is released from rest at the top of the incline and is brought to rest momentarily after compressing the spring by 2 m. If g=10m/s2, the speed of mass just before it touches the spring is √10xm/s. Find value of x?
 View Solution
View SolutionQuestion 144
A block of mass m is connected to a massless pulley and mass-less spring of stiffness k. The pulley is frictionless. The string is mass-less. Initially the spring is unstretched when the block is released. When the spring is maximum stretched, find the ratio of tenstion in the rope and weight of the block.
 View Solution
View SolutionQuestion 145
The potential energy of a particle is determined by the expression U=α(x2+y2), where α is a positive constant. The particle begins to move from a point with the co-ordinates (3, 3) only under the action of potential fields force. When it reaches the point
(1, 1) its kinetic energy is 4Kα. Find the value of K.View SolutionQuestion 146
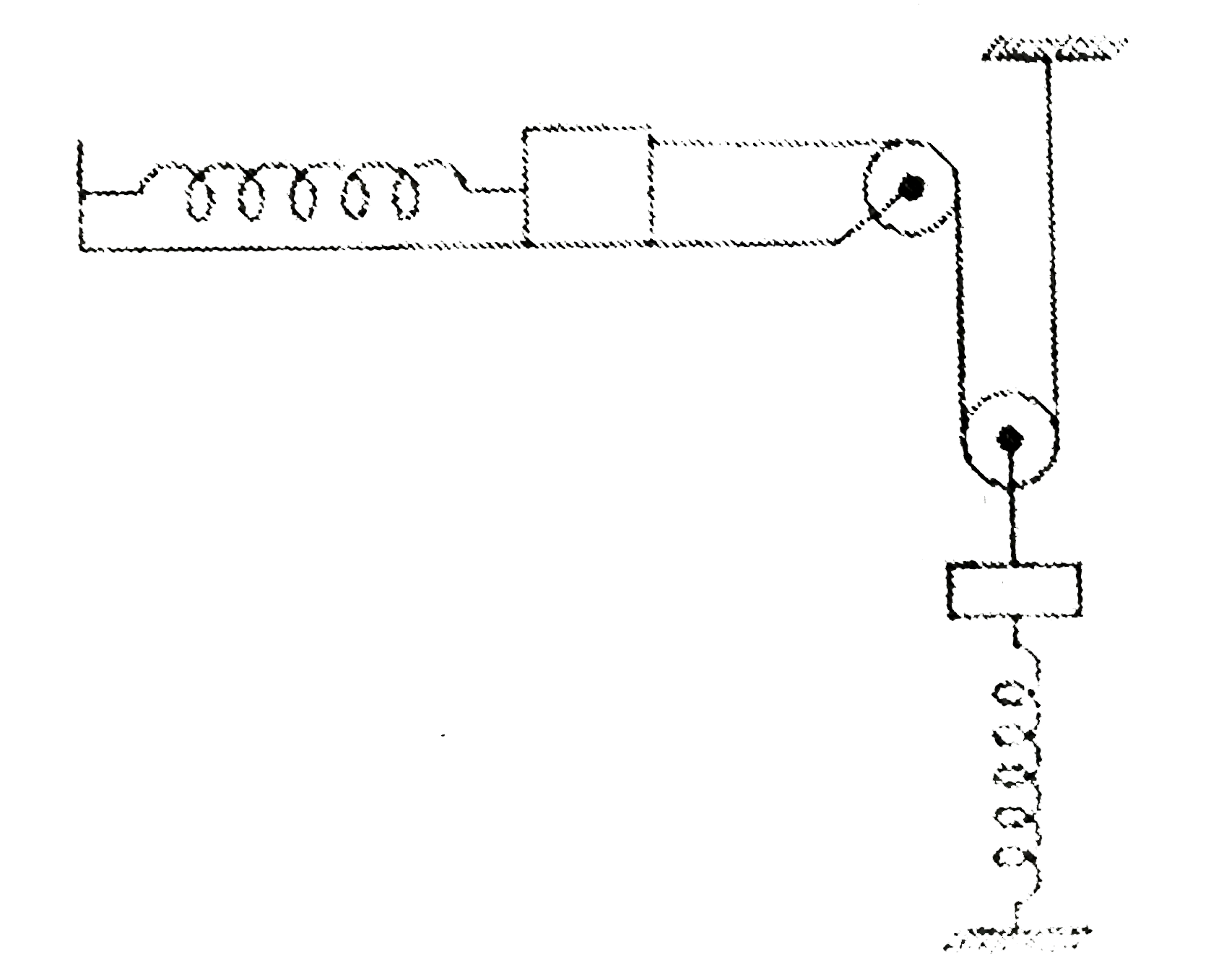
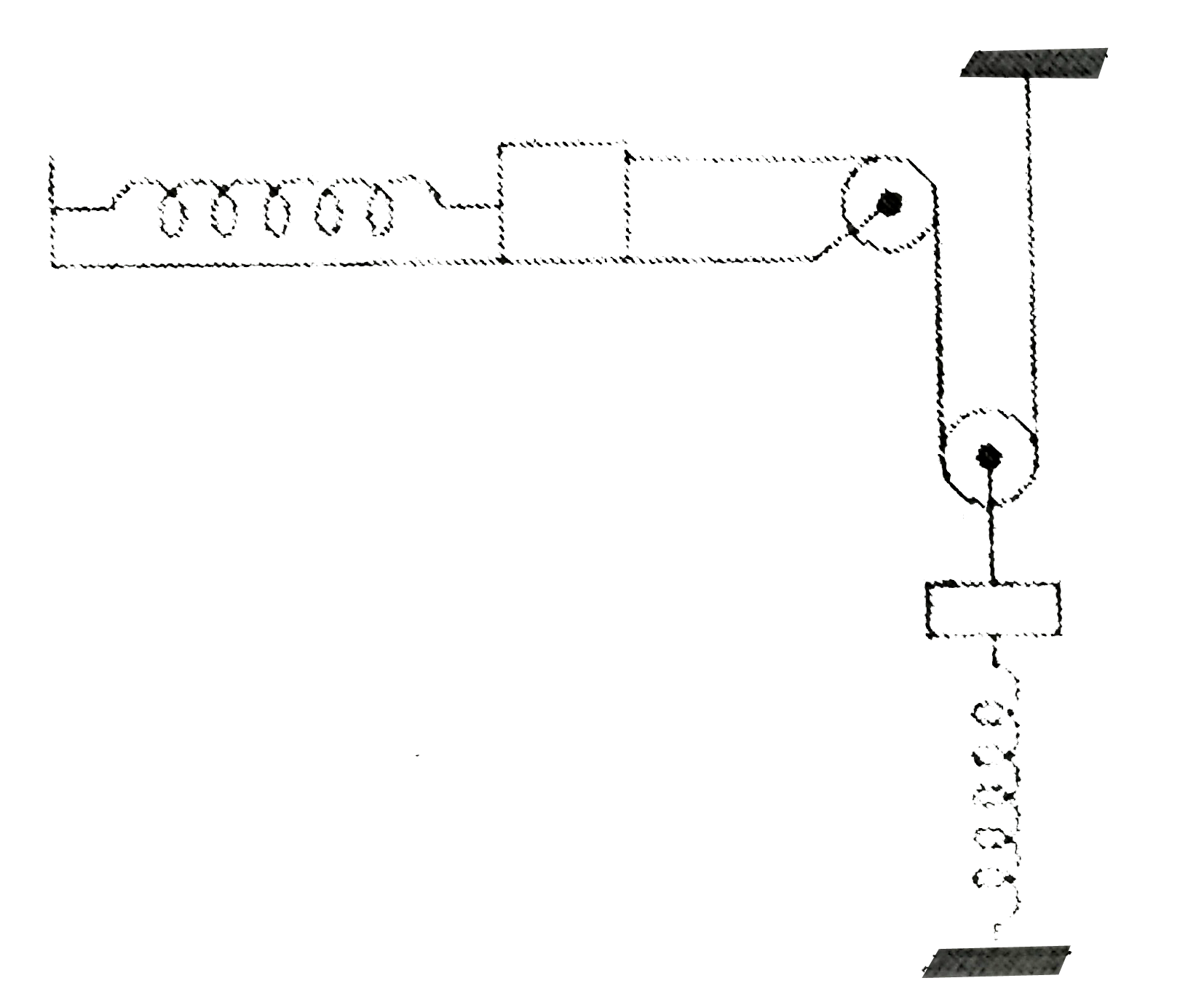
A 10 kg collar P slides with negligible friction on the fixed vertical shaft. When the collar is released from rest at the bottom position shown, it moves up the shaft under the action of the constant force F = 200 N applied to the cable. The position of the small pulley at B is fixed. Find the spring constant k (in k−N/m) which the spring must have if its maximum compression is to be limited to 0.4 m.
 View Solution
View Solution



 .
.

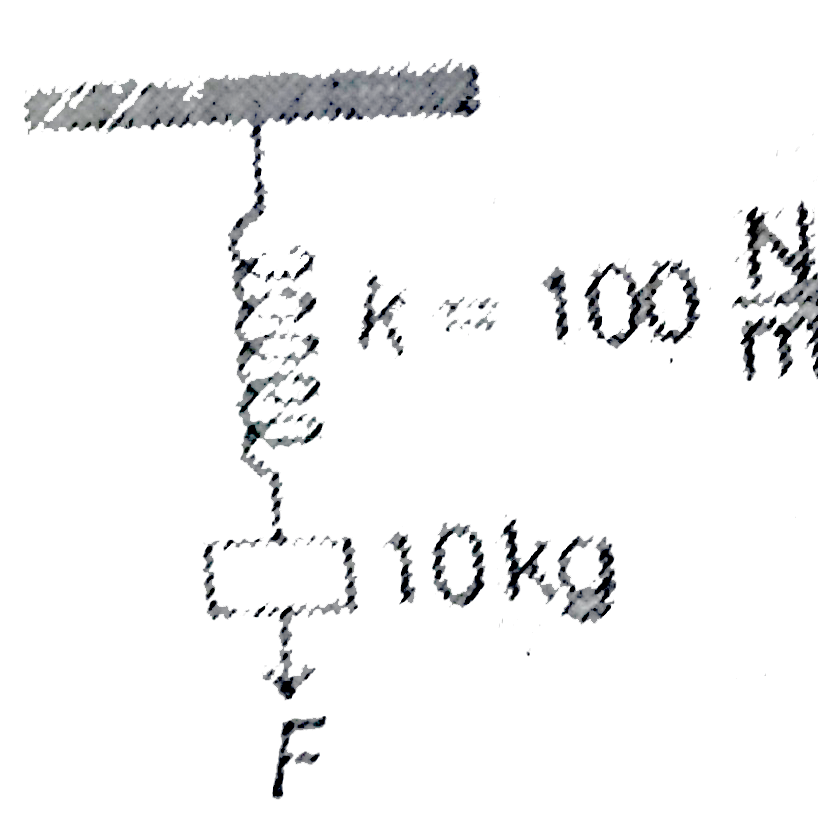

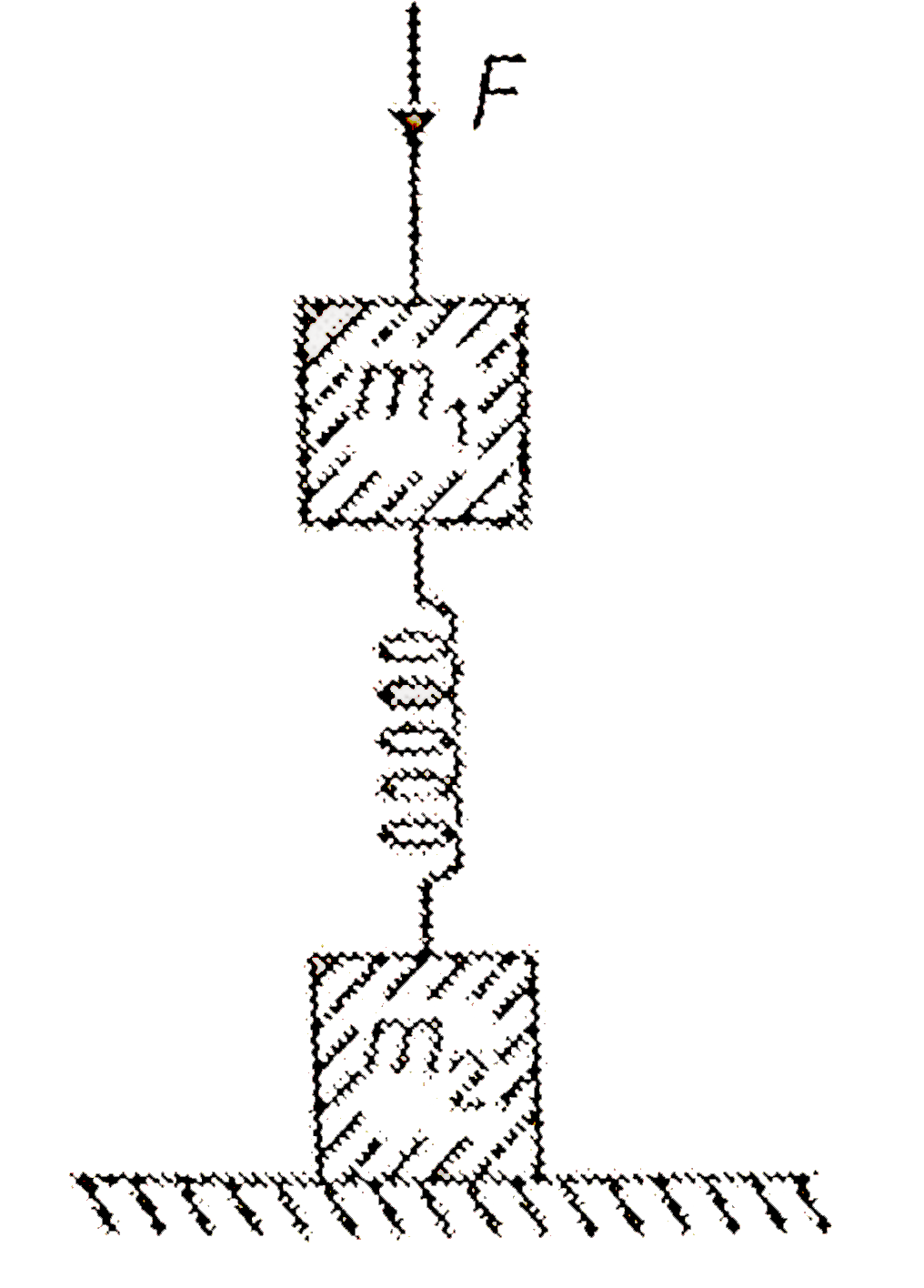
 .
.
 .
. .
.
 .
.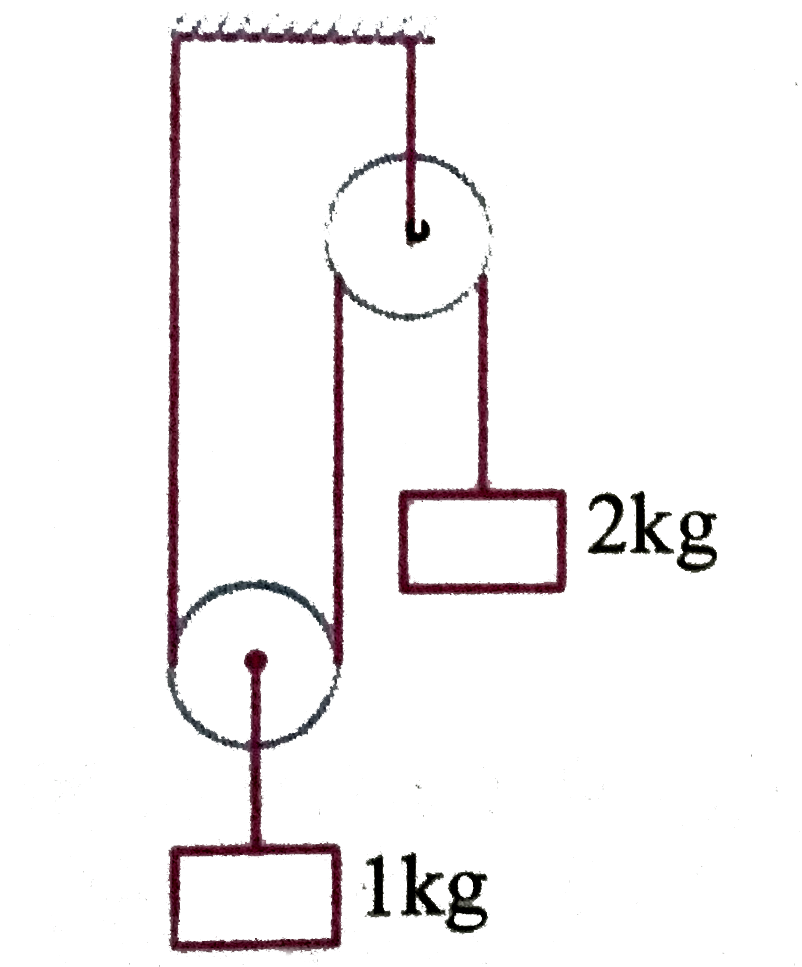 .
.