Exercise 18.3 from DC PANDEY ENGLISH SUPERPOSITION OF WAVES for Class 11

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

A wire is attached to a pan of mass 200 g that contains a 2.0 kg mass as shown in the figure. When plucked, the wire vibrates at a fundamental frequency of 220 Hz. An additional unknown mass M is then added to the pan and a fundamental frequency of 260 Hz is detected. What is the value of M?
.

Question 11

Question 12

Question 13

Question 14

The pulse shown in figure has a speed of $10cm/s$ .

(a) If the linear mass density of the right string is 0.25 that of the left string, at what speed does the transmitted pulse travel?
(b) Compare the heights of the transmitted pulse and the reflected pulse to that of the incident pulse.

Question 15

Question 16

Question 17

Question 18

Question 19

Question 20

Question 21

Question 22

Question 23

Question 24

Question 25

Question 26

Two identical harmonic pulses travelling in opposite directions in a taut string approach each other. At the instant when they completely overlap, the total energy of the string will be
.

Question 27

Question 28

Question 29

Question 30

Question 31

Question 32

Question 33

Question 34

Question 35

Question 36

Question 37

Question 38

Question 39

Question 40

Question 41

Question 42

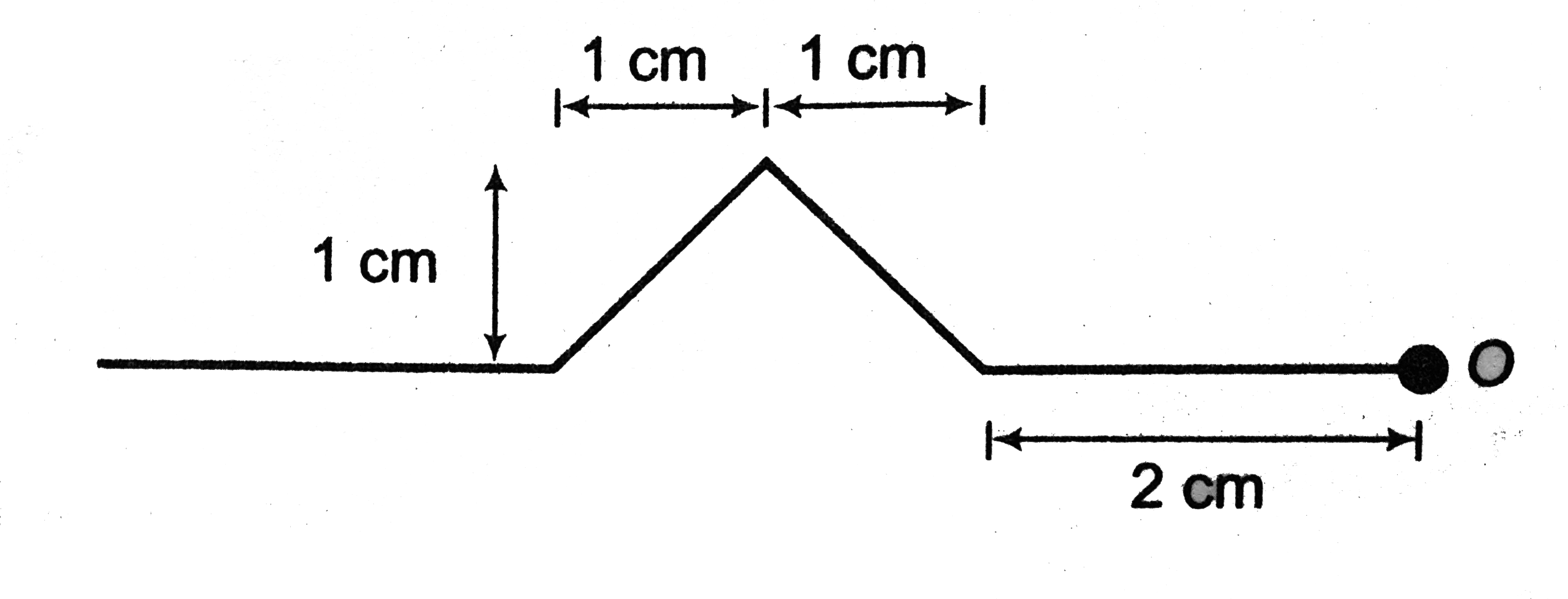
A string of length $20cm$ and linear mass density $0.40g/cm$ is fixed at both ends and is kept under a tension of $16N.A$ wave pulse is produced at $t=0$ nearj an end as shown in figure which travels towards the other end.
when will the string have the shape shown in the figure again? $(\in \times {10}^{-2}s)$

Question 43

A wave pulse on a string has the dimensions shown in figure. The wave speed is $v=1cm/s$.

(a) If point O is a fixed end, draw the resultant wave on the string at t=3 s and t=4 s.
(b) Repeat part (a) for the case in which O is a free end.

Question 44

Question 45

Question 46

Question 47

Question 48

Question 49

Question 50

Question 51

Question 52

Question 53

Question 54

Question 55

Question 56

Question 57

Question 58

Question 59

Figure shows different standing wave patterns on a string of linear mass density $4.0\times {10}^{-2}kg/m$ under a tension of 100 N. The amplitude of antinodes is indicated in each figure. The length of the string is 2.0m.
(i) Obtain the frequencies of the modes shown in figures (a) and (b).
(ii)Write down the transverse displacement y as a function of x and t for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).

Question 60

Question 61

Question 62

Question 63

A string that is 10 cm long is fixed at both ends. At t=0, a pulse travelling from left to right at $1cm/sis4.0cm$ from the right end as shown in figure. Determine the next two times when the pulse will be at that point again. State in each case whether the pulse is upright or inverted .
.

Question 64

Two pulses travelling in opposite directions along a string are shown for $t=0$ in the figure. Plot the shape of the string at t= 1.0, 2.0, 3.0, 4.0 and 5.0s respectively .

Question 65

Question 66

Question 67

Question 68

Question 69

Question 70

Question 71

Question 72

Question 73

Question 74

Question 75

Question 76

Question 77

Question 78

Question 79

Question 80

Question 81

Question 82

Question 83

Question 84

Question 85

Question 86

Question 87

Question 88

Question 89

Question 90

Question 91

Question 92

Question 93

A string tied between $x=0\text{and}x=l$ vibrates in fundamental mode. The amplitude $A$, tension $T$ and mass per unit length $\mu$ is given. Find the total energy of the string.

Question 94

Question 95

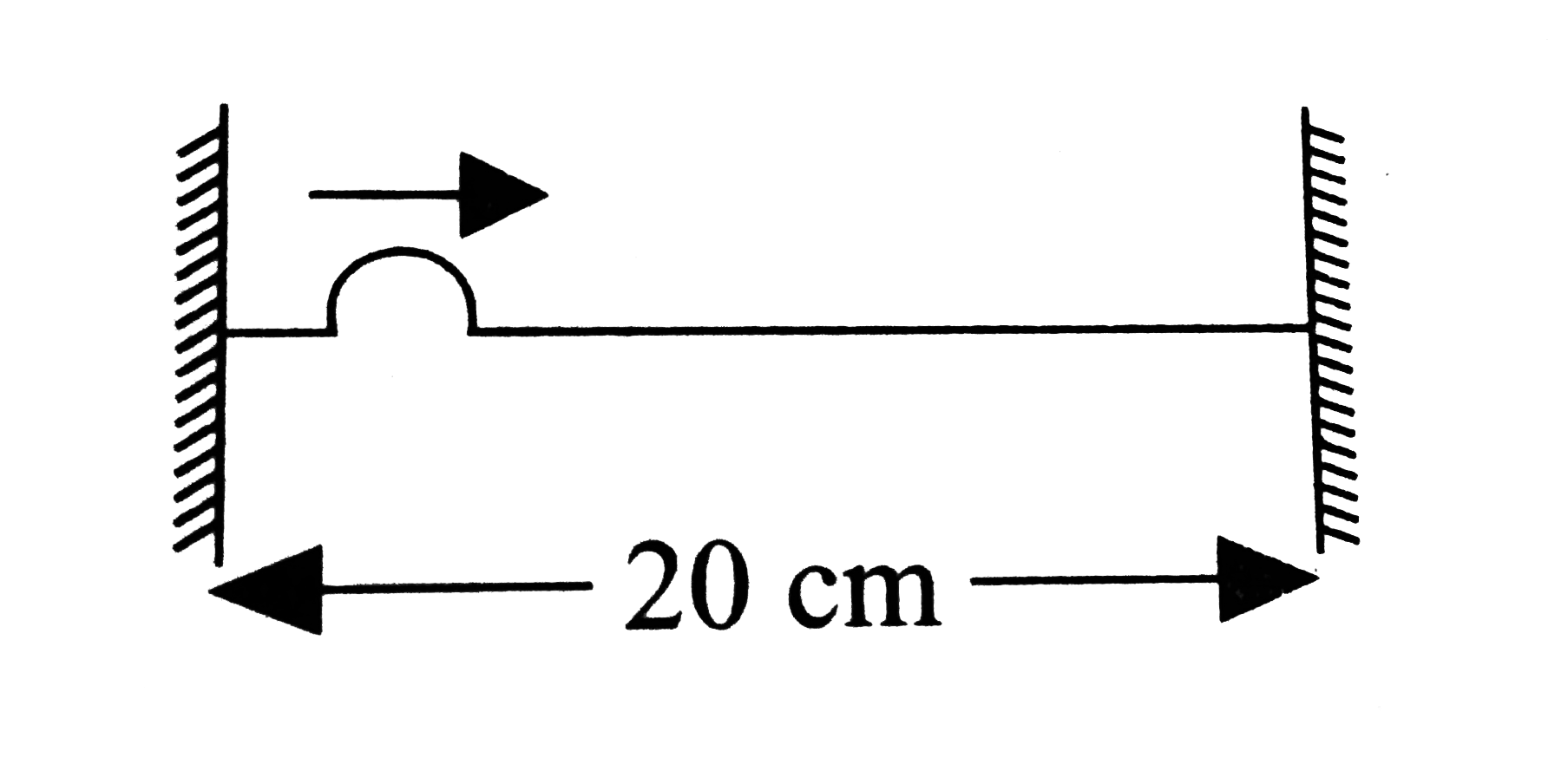
A light string is tied at one end to a fixed support and to a heavy string of equal length $L$ at the other end as shown in figure. A block of mass $m$ is tied to the free end of heavy string. Mass per unit length of the strings are $\mu$ and $9\mu$ and the tension is $T$. Find the possible values of frequencies such that junction of two wire point $A$ is a node.

Question 96

Question 97

Question 98

Question 99

A metal rod of length 1m is clamped at two points as shown in the figure. Distance of the clamp from the two ends are 5 cm and 15 cm, respectively. Find the minimum and next higher frequency of natural longitudinal oscillation of the rod. Given that Young's modulus of elasticity and density of aluminium are $Y=1.6\times {10}^{11}N{m}^{-2}$ and $\rho =2500kg{m}^{-3}$ , respectively.

Question 100