Medical entranes gallery from DC PANDEY ENGLISH Chapter 13 FLUID MECHANICS for Class 11

Question 1

Question 2

A rectangular tube of uniform cross section has three liquids of densities ${\rho }_1,{\rho }_2$ and ${\rho }_3$. Each liquid column has length $l$ equal to length of sides of the equilateral triangle. Find the length $x$ of the liquid of density ${\rho }_1$ in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.

Question 3

Question 4

Question 5

Question 6

In the accompanying figure. Line l passes through the origin and the point (2, 4). Line m (not shown) is perpendicular to line l at (2, 4). Line m intersects the x-axis at which point?

Question 7

Question 8

Question 9

Question 10

Question 11

Question 12

Question 13

Question 14

Question 15

Question 16

Question 17

Question 18

Question 19

Question 20

Question 21

Question 22

Question 23

Question 24

Question 25

Question 26

Question 27

Question 28

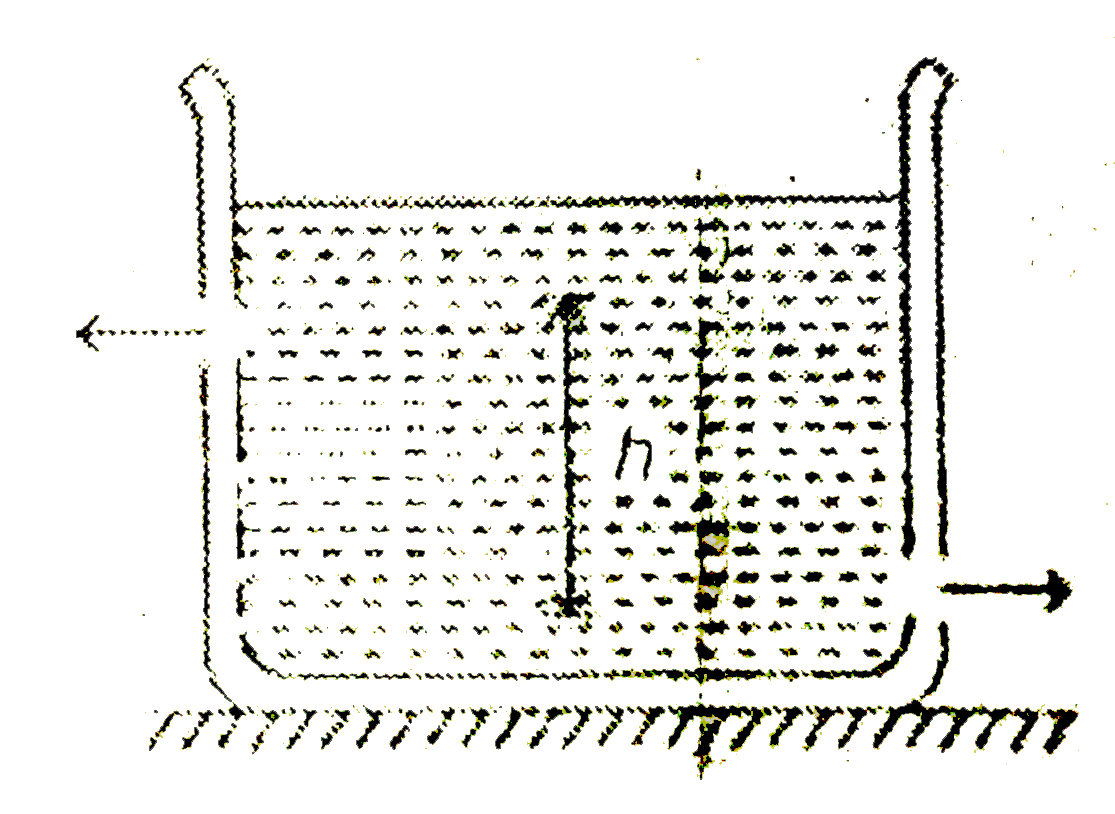
There are two identical small holes of area of cross-section a on the opposite sides of a tank containing a liquid of density $\rho$. The difference in height between the holes is h. Tank is resting on a smooth horizontal surface. Horizontal force on which will have to be applied on the to keep it in equilibrium is

Question 29

Question 30

Question 31

Question 32

Question 33

Question 34

Question 35

Question 36

Question 37

Question 38

Question 39

Question 40

Question 41

Question 42

Question 43

Question 44

Question 45

Question 46

Question 47

Question 48

Question 49