TRIGONOMETRIC EQUATION for Class 11 MATHS

An equation involving one or more trigonometrical ratios of unknown angle is called a trigonometric equation.
e.g., $\cos x=\frac{1}{2};{\sin }^{2}x-4\cos x=1$.
The value of an unknown angle which satisfies the given trigonometric equation is called a solution or root of the equation.
For example: $2\sin \theta =\sqrt{3}$, Clearly $\theta ={60}^{\circ }$ and ${120}^{\circ }$ are solutions of the equation between $0^{\circ }$ and ${360}^{\circ }$.
Now suppose $\tan \theta =1$, then there will be many possible values of $\theta$, so our main ojective is to write down all the solution in short form. Since all trigonometric functions are periodic and therefore solution of all trigonometrical equation can be generalized with the help of periodicity of trigonometrical function.

A value of the unknown angle which satisfies the given equation is called a solution of the trigonometric equation.
( a ) Principal solution :- The solution of the trigonometric equation lying in the interval $[0,2\pi )$.
(b ) General solution :- Since all the trigonometric functions are many one & periodic, hence there are infinite values of $\theta$ for which trigonometric functions have the same value. All such possible values of $\theta$ for which the given trigonometric function is satisfied is given by a general formula. Such a general formula is called general solution of trigonometric equation.
(c) Particular solution :- The solution of the trigonometric equation lying in the given interval.

( a ) If $\sin \theta =0$, then $\theta =n\pi$, $n\in I$(set of integers)
(b) If $\cos \theta =0$, then $\theta =(2n+1)\frac{\pi }{2},n\in I$
(c) If $\tan \theta =0$, then $\theta =n\pi ,n\in I$
(d) If $\sin \theta =\sin \alpha$, then $\theta =n\pi +{(–1)}^n\alpha$ where $\alpha \in [\frac{-\pi }{2},\frac{\pi }{2}],n\in I$
(e) If $\cos \theta =\cos \alpha$, then $\theta =2n\pi \pm \alpha ,n\in I,\alpha \in [0,\pi ]$
(f) If $\tan \theta =\tan \alpha$, then $\theta =n\pi +\alpha ,n\in I,\alpha \in (-\frac{\pi }{2},\frac{\pi }{2})$
( g ) If $\sin \theta =1$, then $\theta =2n\pi +\frac{\pi }{2}=(4n+1)\frac{\pi }{2},n\in I$
(h) If $\cos \theta =1$ then $\theta =2n\pi ,n\in I$
(i) If ${\sin }^2\theta ={\sin }^2\alpha$ or ${\cos }^2\theta ={\cos }^2\alpha$ or ${\tan }^2\theta ={\tan }^2\alpha$, then $\theta =n\pi \pm \alpha ,n\in I$
(j) For $n\in I,\sin n\pi =0$ and $\cos n\pi ={(–1)}^n,n\in I$
$\sin (n\pi +\theta )={(–1)}^n\sin \theta$ , $\cos (n\pi +\theta )={(–1)}^n\cos \theta$
( k ) $\cos n\pi ={(–1)}^n,n\in I$
if n is an odd integer, then $\frac{\sin \left(n\pi \right)}{2}={(-1)}^{\frac{n-1}{2}},\frac{\cos \left(n\pi \right)}{2}=0$
$\sin (\frac{n\pi }{2}+\theta )={(-1)}^{\frac{n-1}{2}}\cos \theta$
$\cos (\frac{n\pi }{2}+\theta )={(-1)}^{\frac{n+1}{2}}\sin \theta$

Find the set of values of x for which $\frac{\tan 3x-\tan 2x}{1+\tan 3x\tan 2x}$ = 1

we have, $\frac{\tan 3x-\tan 2x}{1+\tan 3x\tan 2x}=1\Rightarrow \tan (3x-2x)=1\Rightarrow \tan x=1$
$\Rightarrow \tan x=\tan \left(\frac{\pi }{4}\right)\Rightarrow x=n\pi +\frac{\pi }{4},n\in I$ (using $\tan \theta =\tan \alpha \iff \theta =n\pi +\alpha$)
But for this value of x, tan 2x is not defined.
Hence the solution set for x is $\varphi$

(a) For equations of the type $\sin \theta =k$ or $\cos \theta =k$, one must check that $\left|k\right|\le 1$.
(b) Avoid squaring the equations, if possible, because it may lead to extraneous solutions. Reject extra solutions if they do not satisfy the given equation.
(c) Do not cancel the common variable factor from the two sides of the equations which are in a product because we may loose some solutions.
(d) The answer should not contain such values of $\theta$, which make any of the terms undefined or infinite.
(i) Check that denominator is not zero at any stage while solving equations.
(ii) If $\tan \theta$ or $\sec \theta$ is involved in the equations, $\theta$ should not be odd multiple of $\frac{\pi }{2}$.
(iii) If $\cot \theta$ or $\cos ec\theta$ is involved in the equation, $\theta$ should not be multiple of $\pi$ or 0.

There are following many different strategies for solving trigonometric equations

e.g. $(2\sin x–\cos x)(1+\cos x)={\sin }^{2}x$
$\therefore (2\sin x–\cos x)(1+\cos x)–(1–{\cos }^{2}x)=0$
$\therefore (1+\cos x)(2\sin x–\cos x–1+\cos x)=0$
$\Rightarrow (1+\cos x)(2\sin x–1)=0$
$\Rightarrow \cos x=–1$ or $\sin x=\frac{1}{2}$
$\cos x=–1=\cos \pi \Rightarrow x=2n\pi +\pi =(2n+1)\pi ,n\in I$
or $\sin x=\frac{1}{2}=\sin \left(\frac{\pi }{6}\right)\Rightarrow x=k\pi +{(–1)}^k\frac{\pi }{6},k\in I$

If $\frac{1}{6}\sin \theta ,\cos \theta$ and $\tan \theta$ are in geometric progression, then the solution for $\theta$ is

${\cos }^2\theta =\frac{1}{6}\sin \theta \cdot \tan \theta$
$\Rightarrow {\cos }^2\theta =\frac{1}{6}\left(\frac{{\sin }^2\theta }{\cos \theta }\right)$
$\Rightarrow 6{\cos }^3\theta =1-{\cos }^2\theta$
$\Rightarrow 6{\cos }^3+{\cos }^2\theta -1=0$
$\therefore (2\cos \theta -1)(3{\cos }^2\theta +2\cos \theta +1)=0$
$\Rightarrow \cos \theta =\frac{1}{2}$ (other values of $\cos \theta$ are imaginary)
$\Rightarrow \cos \theta =\cos \left(\frac{\pi }{3}\right)$ $\Rightarrow \theta =2n\pi \pm \frac{\pi }{3},n\in I$

e.g. $6–10\cos x=3{\sin }^{2}x$
$\therefore 6–10\cos x=3–3{\cos }^{2}x\Rightarrow 3{\cos }^{2}x–10\cos x+3=0$
$\Rightarrow (3\cos x–1)(\cos x–3)=0\Rightarrow \cos x=\frac{1}{3}$ or $\cos x=3$
Since $\cos x=3$ is not possible as $–1\le \cos x\le 1$
$\therefore \cos x=\frac{1}{3}=\cos \left({\cos }^{-1}\left(\frac{1}{3}\right)\right)\Rightarrow x=2n\pi \pm {\cos }^{-1}\left(\frac{1}{3}\right),n\in I$

If the equation ${\sin }^2\theta -\cos \theta =\frac{1}{4},$ then the value of $\theta$ lying in the interval $0\le \theta \le 2\pi$ is

The given equation can be written as
$1-{\cos }^2\theta -\cos \theta =\frac{1}{4}$
$\Rightarrow {\cos }^2\theta +\cos \theta =\frac{3}{4}=0$
$\Rightarrow 4{\cos }^2\theta +4\cos \theta -3=0$
$\Rightarrow \cos \theta =\frac{-4\pm \sqrt{16+48}}{8}=\frac{-4\pm 8}{8}=\frac{1}{2},-\frac{3}{2}$
Since , $\cos \theta =-\frac{3}{2}$ is not possible as $-1\le \cos \theta \le 1$ ,so we take
$\therefore \cos \theta =\frac{1}{2}=\text{cos}\frac{\pi }{3}\Rightarrow \theta =2n\pi \pm \frac{\pi }{3}$ ...(i)
For the given interval ,put n = 0 and n = 1 in EQ . (i) , we get
$\theta =\frac{\pi }{3},\frac{5\pi }{3}$

The number of solutions of the equation $\tan x+\sec x=2\cos x$ lying in the interval $[0,2\pi ]$

$\tan x+\sec x=2\cos x$
$\Rightarrow \frac{\sin x}{\cos x}+\frac{1}{\cos x}=2\cos x$
$\Rightarrow 1+\sin x=2{\cos }^{2}x$
$\Rightarrow 1+\sin x=2(1-{\sin }^{2}x)$
$\Rightarrow 1+\sin x=2-2{\sin }^{2}x$
$\Rightarrow 2{\sin }^{2}x+\sin x-1=0$
$\Rightarrow 2{\sin }^{2}x+2\sin x-\sin x-1=0$
$\Rightarrow 2\sin (\sin x+1)-1(\sin x+1)=0$
$\Rightarrow (2\sin x-1)(\sin x+1)=0$
$\Rightarrow \sin x=\frac{1}{2}\text{or}\sin x=-1$
$\Rightarrow x=\frac{\pi }{6},\frac{5\pi }{6}\text{or}x=\frac{3\pi }{2}$
But, $x=\frac{3\pi }{2}$ is not possible as original equation have $\tan \theta$ and $\tan \left(\frac{3\pi }{2}\right)=-\infty .$
$\therefore .x=\frac{\pi }{6},\frac{5\pi }{6}$
So, there are $2$ solutions for $x$ are possible.

Consider, $a\sin \theta +b\cos \theta =c$ .............. (i)
$\therefore$ $\frac{a}{\sqrt{a^2+b^2}}\cdot \sin \theta$ + $\frac{b}{\sqrt{a^2+b^2}}\cdot \cos \theta$ $=\frac{c}{\sqrt{a^2+b^2}}$
equation (i) has a solution only if $\left|c\right|\le \sqrt{a^2+b^2}$
let $\frac{a}{\sqrt{a^2+b^2}}=\cos \varphi ,\frac{b}{\sqrt{a^2+b^2}}=\sin \varphi$ and $\varphi ={\tan }^{-1}\left(\frac{b}{a}\right)$
by introducing this auxillary argument $\varphi$, equation (i) reduces to
$\sin (\theta +\varphi )=\frac{c}{\sqrt{a^2+\left(b^2\right)}}$, now this equation can be solved easily.

Prove that the equation kcosx – 3sinx = k + 1 possess a solution iff $k\in (–\infty ,4]$.

Here , $k\cos x-3\sin x=k+1$, could be re-written as :
$\frac{k}{\sqrt{k^2+9}}\cdot \cos x-\frac{3}{\sqrt{k^2+9}}\cdot \sin x=\frac{k+1}{\sqrt{k^2+9}}$
or $\cos (x+\varphi )=\frac{k+1}{\sqrt{k^2+9}}$ , where $\tan \varphi \frac{3}{k}$
which possess a solution only if $-1\le \frac{k+1}{\sqrt{k^2+9}}\le 1$
i.e., $\left|\frac{k+1}{\sqrt{k^2+9}}\right|\le 1$
i.e., ${(k+1)}^2\le k^2+9$
i.e., $k^2+2k+1\le k^2+9$
$k\le 4$
$\Rightarrow$ the interval of k for which the equation (kcosx - 3sinx = k+1) has a solution is $(-\infty ,4]$

e.g. $\cos 3x+\sin 2x–\sin 4x=0$
$\cos 3x–2\sin x\cos 3x=0$
$\Rightarrow \left(\cos 3x\right)(1–2\sin x)=0$
$\Rightarrow \cos 3x=0$ or $\sin x=\frac{1}{2}$
$\Rightarrow \cos 3x=0=\cos \left(\frac{\pi }{2}\right)$ or $\sin x=\frac{1}{2}=\sin \left(\frac{\pi }{6}\right)$
$\Rightarrow 3x=2n\pi \pm \left(\frac{\pi }{2}\right)$ or $x=m\pi +{(-1)}^m\cdot \left(\frac{\pi }{6}\right)$
$x=\frac{2n\pi }{3}\pm \left(\frac{\pi }{6}\right)$ or $x=m\pi +{(-1)}^m\left(\frac{\pi }{6}\right)$; $(n,m\in I)$

Solve : $\cos \theta +\cos 3\theta +\cos 5\theta +\cos 7\theta =0$

We have $\cos \theta +\cos 7\theta +\cos 3\theta +\cos 5\theta =0$
$\Rightarrow 2\cos 4\theta \cos 3\theta +2\cos 4\theta \cos \theta =0\Rightarrow \cos 4\theta (\cos 3\theta +\cos \theta )=0$
$\Rightarrow \cos 4\theta \left(2\cos 2\theta \cos \theta \right)=0$
Either $\Rightarrow \cos \theta =0\Rightarrow \theta =(2n_1+1)\frac{\pi }{2},n_1\in I$
or $\cos 2\theta =0\Rightarrow \theta =(2n_2+1)\left(\frac{\pi }{4}\right),n_2\in I$
$\cos 4\theta =0\Rightarrow \theta =(2n_3+1)\left(\frac{\pi }{8}\right),n_3\in I$

e.g. $\sin 5x.\cos 3x=\sin 6x.\cos 2x$
$\sin 8x+\sin 2x=\sin 8x+\sin 4x$
$\therefore 2\sin 2x.\cos 2x–\sin 2x=0$
$\Rightarrow \sin 2x(2\cos 2x–1)=0$
$\Rightarrow \sin 2x=0$ or $\cos 2x=\frac{1}{2}$
$\Rightarrow \sin 2x=0=\sin 0$ or $\cos 2x=\frac{1}{2}=\cos \left(\frac{\pi }{3}\right)$
$\Rightarrow 2x=n\pi +{(-1)}^{n}0,n\in I$ or $2x=2m\pi \pm \left(\frac{\pi }{3}\right),m\in I$
$x=\frac{n\pi }{2},n\in I$ or $x=m\pi \pm \left(\frac{\pi }{6}\right),m\in I$

Solve :
$\cos \theta \cos 2\theta \cos 3\theta =\frac{1}{4}$: where $(0\le \theta \le \pi )$

$\frac{1}{2}\left(2\cos \theta \cos 3\theta \right)\cos 2\theta =\frac{1}{4}\Rightarrow (\cos 2\theta +\cos 4\theta )\cos 2\theta =\frac{1}{2}$
$\Rightarrow \frac{1}{2}[2{\cos }^{2}2\theta +2\cos 4\theta \cos 2\theta ]=\frac{1}{2}\Rightarrow 1+\cos 4\theta +2\cos 4\theta \cos 2\theta =1$
$\therefore \cos 4\theta (1+2\cos 2\theta )=0$
$\cos 4\theta =0$ or $(1+2\cos 2\theta )=0$
Now from the first equation : $2\cos 4\theta =0=\cos \left(\frac{\pi }{2}\right)$
$\therefore 4\theta =(n+\frac{1}{2})\pi \Rightarrow \theta =(2n+1)\frac{\pi }{8},n\in I$
for $n=0$, $\theta =\frac{\pi }{8}$; $n=1$,$\theta =\frac{3\pi }{8}$;$n=2$,$\theta =\frac{5\pi }{8}$;n=3, $\theta =\frac{7\pi }{8}$ $(\because 0\le \theta \le \pi )$
and from the second equation :
$\cos 2\theta =-\frac{1}{2}=-\cos \left(\frac{\pi }{3}\right)=\cos (\pi -\frac{\pi }{3})=\cos \left(\frac{2\pi }{3}\right)$
$\therefore 2\theta =2k\pi \pm \frac{2\pi }{3}$
$\therefore \theta =k\pi \pm \frac{\pi }{3},k\in I$
again for k =0, $\theta =\frac{\pi }{3}$; $k=1$,$\theta =\frac{2\pi }{3}$ $(\because 0\le \theta \le \pi )$
$\therefore \theta =\frac{\pi }{8},\frac{\pi }{3},\frac{3\pi }{8},\frac{5\pi }{8},\frac{2\pi }{3},\frac{7\pi }{8}$

(i) Equations of the form P (sin x ± cos x, sin x. cos x) = 0, where P (y,z) is a polynomial, can be solved by the substitution :
$\cos x\pm \sin x=t\Rightarrow 1\pm 2\sin x.\cos x=t^2$.
e.g. $\sin x+\cos x=1+\sin x.\cos x$.
put $\sin x+\cos x=t$
$\Rightarrow {\sin }^{2}x+{\cos }^{2}x+2\sin x.\cos x=t^2$
$\Rightarrow 2\sin x.\cos x=t^2-1(\because {\sin }^2+{\cos }^{2}x=1)$
$\Rightarrow \sin x.\cos x=\left(\frac{t^2-1}{2}\right)$
Substituting above result in given equation, we get :
$t=1+\left(\frac{t^2-1}{2}\right)$
$\Rightarrow 2t=t^2+1\Rightarrow t^2-2t+1=0$
$\Rightarrow {(t-1)}^2=0\Rightarrow t=1$
$\Rightarrow \sin x+\cos x=1$
Dividing both sides by $\sqrt{1^2+1^2}$ i.e. $\sqrt{2}$, we get
$\Rightarrow \frac{1}{\sqrt{2}}\sin x+\frac{1}{\sqrt{2}}\cos x=\frac{1}{\sqrt{2}}\Rightarrow \cos x\cos \left(\frac{\pi }{4}\right)+\sin x.\sin \left(\frac{\pi }{4}\right)=\frac{1}{\sqrt{2}}$
$\cos (x-\frac{\pi }{4})=\cos \left(\frac{\pi }{4}\right)\Rightarrow x-\frac{\pi }{4}=2n\pi \pm \frac{\pi }{4}$
$\Rightarrow x=2n\pi \text{or}x=2n\pi +\frac{\pi }{2}=(4n+1)\frac{\pi }{2},n\in I$
(ii) Equations of the form of $a\sin x+b\cos x+d=0$, where a, b & d are real numbers can be solved by changing sin x & cos x into their corresponding tangent of half the angle.
e.g. $3\cos x+4\sin x=5$
$\Rightarrow 3\left(\frac{1-{\tan }^2\left(\frac{x}{2}\right)}{1+{\tan }^2\left(\frac{x}{2}\right)}\right)+4\left(\frac{2\tan \left(\frac{x}{2}\right)}{1+{\tan }^2\left(\frac{x}{2}\right)}\right)=5$
$\Rightarrow \frac{3-3\cdot {\tan }^2\left(\frac{x}{2}\right)}{1+{\tan }^2\left(\frac{x}{2}\right)}+\frac{8\tan \left(\frac{x}{2}\right)}{1+{\tan }^2\left(\frac{x}{2}\right)}=5$
$\Rightarrow 3-3\cdot {\tan }^2\left(\frac{x}{2}\right)+8\cdot \tan \left(\frac{x}{2}\right)=5+5\cdot {\tan }^2\left(\frac{x}{2}\right)\Rightarrow 8\cdot {\tan }^2\left(\frac{x}{2}\right)-8\cdot \tan \left(\frac{x}{2}\right)+2=0$
$\Rightarrow 4\cdot {\tan }^2\left(\frac{x}{2}\right)-4\cdot \tan \left(\frac{x}{2}\right)+1=0\Rightarrow {(2\tan \cdot \frac{x}{2}-1)}^2=0$
$\Rightarrow 2\tan \left(\frac{x}{2}\right)-1=0\Rightarrow \tan \left(\frac{x}{2}\right)=\frac{1}{2}=\tan \left({\tan }^{-1}\left(\frac{1}{2}\right)\right)$
$\frac{x}{2}=n\pi +{\tan }^{-1}\left(\frac{1}{2}\right),n\in I\Rightarrow x=2n\pi +\left(2{\tan }^{-1}\left(\frac{1}{2}\right)\right),n\in I$
(iii) Many equations can be solved by introducing a new variable.
e.g. ${\sin }^{4}2x+{\cos }^{4}2x=\sin 2x.\cos 2x$
substituting $\sin 2x.\cos 2x=y\because {({\sin }^{2}2x+{\cos }^{2}2x)}^2={\sin }^{4}2x+{\cos }^{4}2x+2{\sin }^{2}2x.{\cos }^{2}2x$
$\Rightarrow {\sin }^{4}2x+{\cos }^{4}2x=1-2{\sin }^{2}2x.{\cos }^{2}2x$ substituting above result in given equation :
$1–2y^2=y$
$\Rightarrow 2y^2+y–1=0\Rightarrow 2(y+1)(y-\frac{1}{2})=0$
$\Rightarrow$y = -1$\text{or}y=\frac{1}{2}\Rightarrow \sin 2x.\cos 2x=–1\text{or}\sin 2x.\cos 2x=\frac{1}{2}$
$\Rightarrow 2\sin 2x.\cos 2x=–2\text{or}2\sin 2x.\cos 2x=1$
$\sin 4x=–2$ (which is not possible) or $2\sin 2x.\cos 2x=1$
$\sin 4x=1=\sin \left(\frac{\pi }{2}\right)\Rightarrow 4x=n\pi +{(–1)}^n\frac{\pi }{2},n\in I$ $\Rightarrow x=\frac{n\pi }{4}+{(-1)}^n\frac{\pi }{8},n\in I$

find the general solution of equation ${\sin }^{4}x+{\cos }^{4}x=\sin x\cos x$

using half angle formulae, we can represent given equation in the form :
${\left(\frac{1-\cos 2x}{2}\right)}^2+{\left(\frac{1+\cos 2x}{2}\right)}^2=\sin x\cos x$
$\Rightarrow {(1-\cos 2x)}^2+{(1+\cos 2x)}^2=4\sin x\cos x$
$\Rightarrow 2(1+{\cos }^{2}2x)=2\sin 2x\Rightarrow 1+1-{\sin }^{2}2x=\sin 2x$
$\Rightarrow {\sin }^{2}2x+\sin 2x=2$
$\Rightarrow \sin 2x=1\text{or}\sin 2x=-2$ (which is not possible)
$\Rightarrow 2x=2n\pi +\frac{\pi }{2},n\in I$
$\Rightarrow x=n\pi +\frac{\pi }{4},n\in I$

e.g. $\sin x(\text{cos}\frac{x}{4}-2\sin x)+(1+\text{sin}\frac{x}{4}-2\cos x)\cos x=0$.
$\therefore \sin x\cdot \text{cos}\frac{x}{4}+\cos x\cdot \text{sin}\frac{x}{4}+\cos x=2$
$\therefore \text{sin}\frac{5x}{4}+\cos x=2$
$\Rightarrow \text{sin}\frac{5x}{4}=1\text{and}\cos x=1$ (as $\sin \theta \le 1\&\cos \theta \le 1$)
Now consider
$\cos x=1\Rightarrow x=2\pi ,4\pi ,6\pi ,8\pi$ .......
and $\text{sin}\frac{5x}{4}=1\Rightarrow x=\frac{2\pi }{5},\frac{10\pi }{5},\frac{18\pi }{5}$.........
Common solution to above APs will be the AP having First term = $2\pi$
Common difference = LCM of $2\pi$ and $\frac{8\pi }{5}=\frac{40\pi }{5}=8\pi$
General solution will be general term of this AP i.e. $2\pi +\left(8\pi \right)n,n\in I$
$\Rightarrow x=2(4n+1)\pi ,n\in I$

Solve the equation ${(\sin x+\cos x)}^{1+2\sin x}=2,when0\le x\le \pi$

We know, - $\sqrt{a^2+b^2}\le a\sin \theta +b\cos \theta \le \sqrt{a^2+b^2}\text{and}-1\le \sin \theta \le 1.$
$\therefore (\sin x+\cos x)$ admits the maximum value as $\sqrt{2}$
and $(1+\sin 2x)$ admits tha maximum value as 2.
also ${\left(\sqrt{2}\right)}^2=2$.
$\therefore$ the equation could hold only when, $\sin x+\cos x=\sqrt{2}\text{and}1+\sin 2x=2$
Now, $\sin x+\cos x=\sqrt{2}\Rightarrow \cos (\text{x}-\frac{\pi }{4})=1$
$\Rightarrow x=2n\pi +\frac{\pi }{4},n\in I$.....(i)
and $1+\sin 2x=2\Rightarrow \sin 2x=1=\sin \left(\frac{\pi }{2}\right)$
$\Rightarrow 2x=m\pi +{(-1)}^m\left(\frac{\pi }{2}\right),m\in I\Rightarrow x=\frac{m\pi }{2}+{(-1)}^m\left(\frac{\pi }{4}\right)$.....(ii)
the value of x in $[0,\pi ]$ satisfying equations (i) and (ii) is $x=\frac{\pi }{4}$ (when n =0 & m =0)
Note $\sin x+\cos x=-\sqrt{2}$ and 1+ sin2x = 2 also satisfies but as $x\ge 0$, this solution is not in domain.

There is no general rule to solve trigonometric inequations and the same rules of algebra are valid provided the domain and range of trigonometric function should be kept in mind.

Solve the following equation, ${\tan }^2\theta +{\sec }^2\theta +3=2(\sqrt{2}\sec \theta +\tan \theta )$

We have ${\tan }^2\theta +{\sec }^2\theta +3=2\sqrt{2}\sec \theta +2\tan \theta$
$\Rightarrow {\tan }^2\theta +1-2\tan \theta +{\sec }^2\theta -2\sqrt{2}\sec \theta +2=0$
$\Rightarrow {(\tan \theta -1)}^2+{(\sec \theta -\sqrt{2})}^2=0\Rightarrow \tan \theta =1$ and $\sec \theta =\sqrt{2}$
As the periodicity of $\tan \theta$ and $\sec \theta$ are not same, we get
$\therefore =2n\pi +\frac{\pi }{4},n\in I$

Find the solution set of equation $5^{(1+{\log }_5\cos x)}=5/2$

Taking log to base 5 on both sides in given equations:
$(1+{\log }_5\cos x).{\mathrm{Log}}_{5}5={\log }_5(5/2)\Rightarrow {\log }_{5}5+{\log }_5\cos x={\log }_{5}5-{\log }_{5}2$
$\Rightarrow {\log }_5\cos =-{\log }_{5}2\Rightarrow \cos x=1/2\Rightarrow x=2n\pi \pm \frac{\pi }{3},n\in I$ Ans.

Find the values of x in the interval $[0,2\pi ]$ which satisfy the inequality:
$3|2\sin x-1|\ge 3+4{\cos }^{2}x$

The given inequality can be written as:
$3|2\sin x-1|\ge 3+4(1-{\sin }^{2}x)\Rightarrow 3|2\sin x-1|\ge 7-4{\sin }^{2}x$
Let $\sin x=t\Rightarrow |\frac{3}{2}t-1|\ge 7-4t^2$
Case I: For $2t-1\ge 0$ i.e., $t\ge 1/2$ we have,$|2t-1|=(2t-1)$
$\Rightarrow 3(2t-1)\ge 7-4t^2\Rightarrow 6t-3\ge 7-4t^2$
$\Rightarrow 4t^2+6y-10\ge 0\Rightarrow 2t^2+3t-5\ge 0$
$\Rightarrow (t-1)(2t+5)\ge 0\Rightarrow t\le -\frac{5}{2}$ and $t\ge 1$
Now for $t\ge \frac{1}{2}$, we get $t\ge 1$ from above conditions i.e., $\sin x\ge 1$
The inequality holds true for x satisfying the equation $\sin x=1\therefore x=\frac{\pi }{2}$
(for $x\in [0,2\pi ])$
Case II: For $2t-t<0\Rightarrow t<\frac{1}{2}$
We have, $|2t-1<0|\Rightarrow t<\frac{1}{2}$
We have, $|2t-1|=-(2t-1)$
$\Rightarrow -3(2t-1)\ge 7-4t^2\Rightarrow -6t+3\ge 7-4t^2$
$\Rightarrow 4t^2-6t-4\ge 0\Rightarrow 2t^2-3t-2\ge 0$
$\Rightarrow (t-2)(2t+1)\ge 0\Rightarrow t\le -\frac{1}{2}$ and $t\ge 2$
Again for $t<\frac{1}{2}$, we get $t\le -\frac{1}{2}$ from above conditions
i.e., $\sin x\le \frac{1}{2}\Rightarrow \frac{7\pi }{6}\le x\le \frac{11}{6}\pi$ (for $x\in [0,2\pi ])$
Thus, $x\in [\frac{7\pi }{6},\frac{11\pi }{6}]\cup \left\{\frac{\pi }{2}\right\}$ Ans.

Find the values of $\theta$, for which $\cos 3\theta +\sin 3\theta +(2\sin 2\theta -3)(\sin \theta -\cos \theta )$ is always positive.

Given expression can be written as:
$4{\cos }^3\theta -3\cos \theta +3\sin \theta -4{\sin }^3\theta +(2\sin 2\theta -3)(\sin \theta -\cos \theta )$
Applying given condtions, we get
$\Rightarrow -4({\sin }^3\theta -{\cos }^3\theta )+3(\sin \theta -\cos \theta )+(\sin \theta -\cos \theta )(2\sin 2\theta -3)>0$
$\Rightarrow -4(\sin \theta -\cos \theta )({\sin }^2\theta +{\cos }^2\theta +\sin \theta \cos \theta )+3(\sin \theta -\cos \theta )+(\sin \theta -\cos \theta )(2\sin 2\theta -3)>0$
$\Rightarrow (\sin \theta -\cos \theta )\{-4-4\sin \theta \cos \theta +3+4\sin \theta -3\}>0$
$\Rightarrow -4(\sin \theta -\cos \theta )>0$
$\Rightarrow -4\sqrt{2}\sin (\theta -\frac{\pi }{4})>0\Rightarrow \sin (\theta -\frac{\pi }{4})<0\Rightarrow 2n\pi -\pi <\theta -\frac{\pi }{4}<2n\pi ,n\in I$
$\Rightarrow 2n\pi -\frac{3\pi }{4}<\theta <2n\pi +\frac{\pi }{4}\Rightarrow \theta \in (2n\pi -\frac{3\pi }{4},2n\pi +\frac{\pi }{4}),n\in I$ Ans.

The number of values of x in the interval $[0,5\pi ]$ satisfying the equation.
$3{\sin }^{2}x-7\sin x+2=0$ is-

$3{\sin }^{2}x-7\sin x+2=0$
$\Rightarrow (3\sin x-1)(\sin x-2)=0$
$\therefore \sin x\ne 2$
$\Rightarrow \sin x=\frac{1}{3}=\sin \alpha$ (say)
Where $\alpha$ is the least positive value of x
such that $\sin \alpha =\frac{1}{3}$

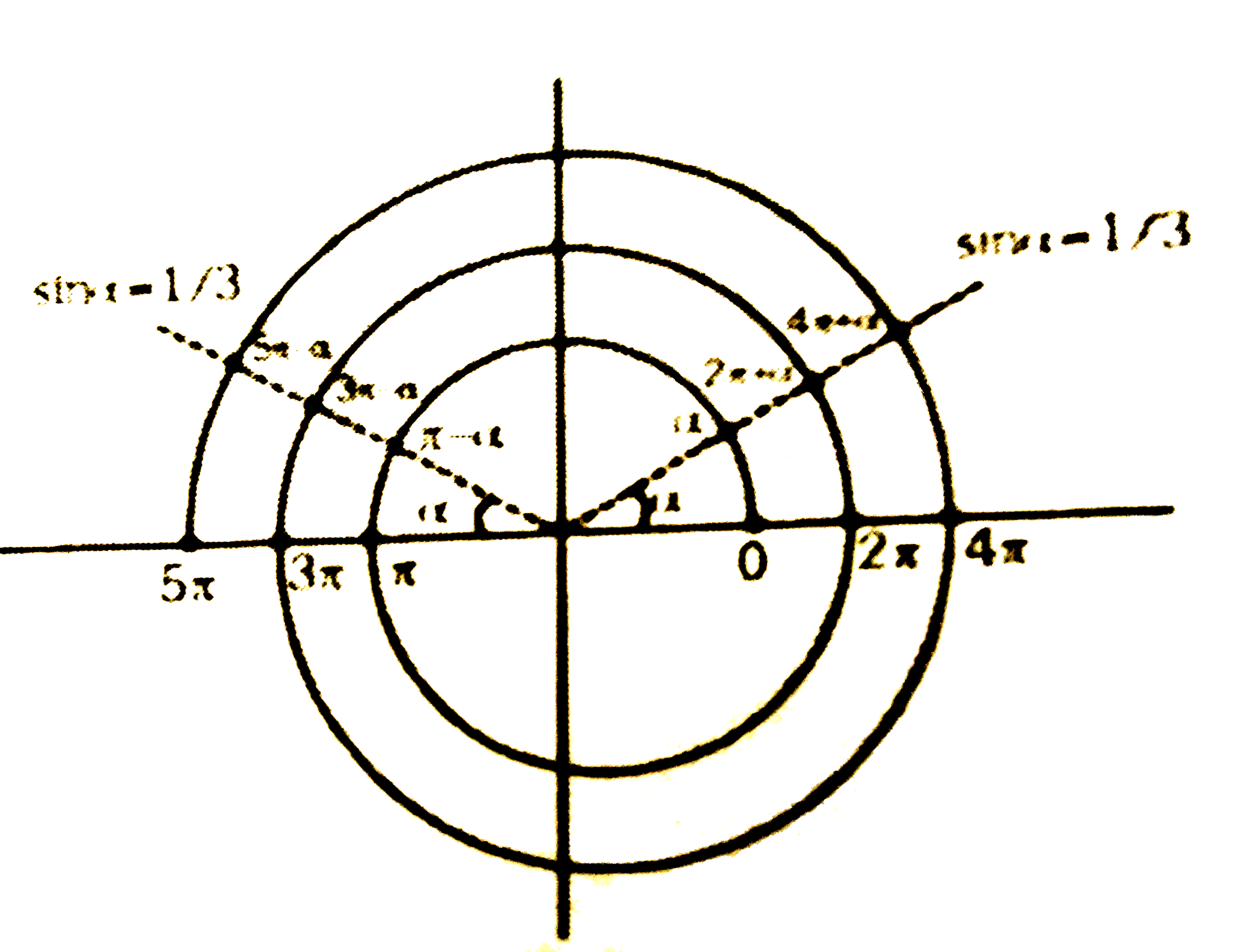
Clearly, $0<\alpha <\frac{\pi }{2}$. We get the solution,
$x=\alpha ,\pi -\alpha ,2\pi +\alpha ,4\pi +\alpha$ and $5\pi -\alpha$
Hence total six values in $[0,5\pi ]$ Ans.